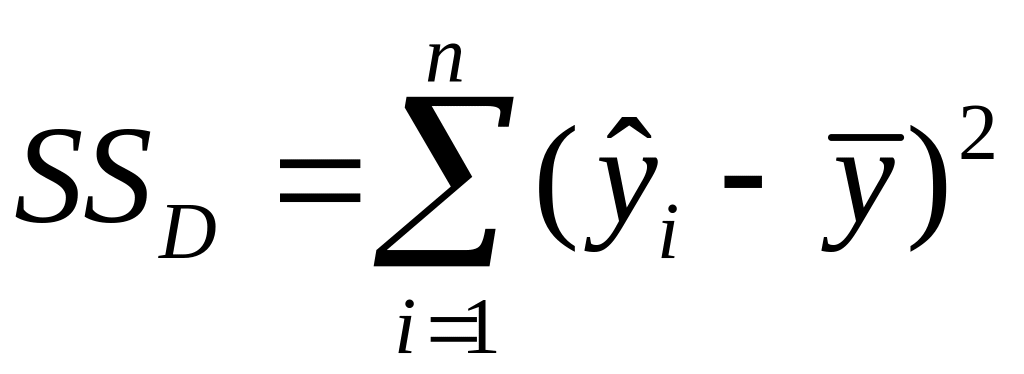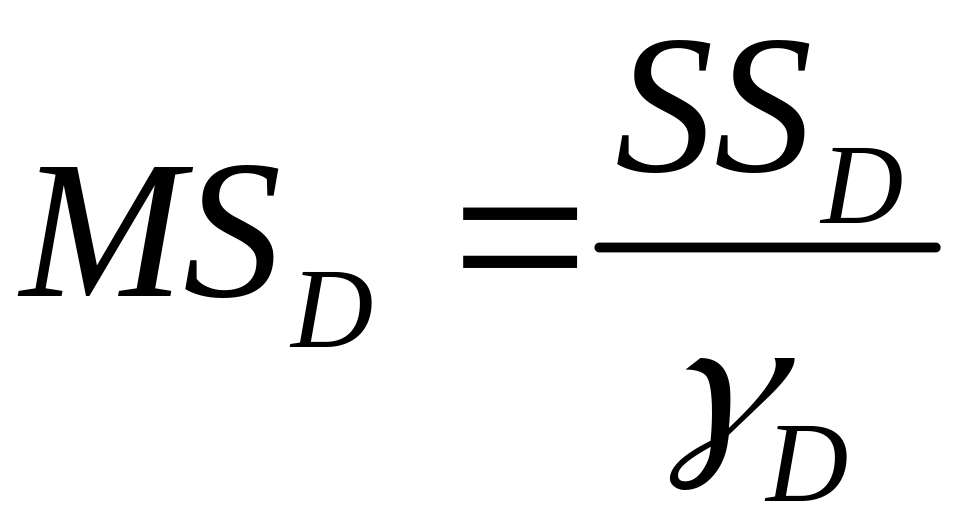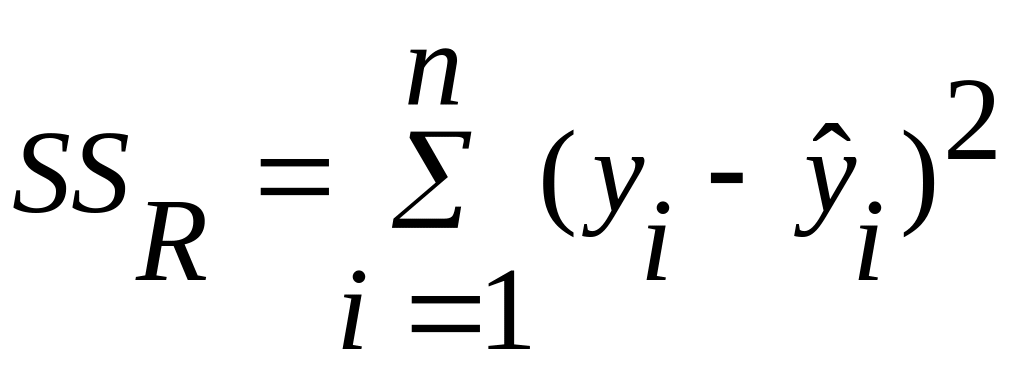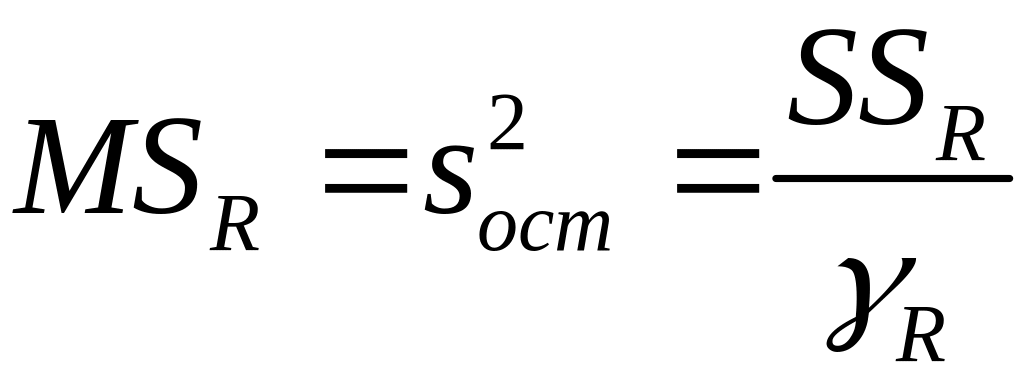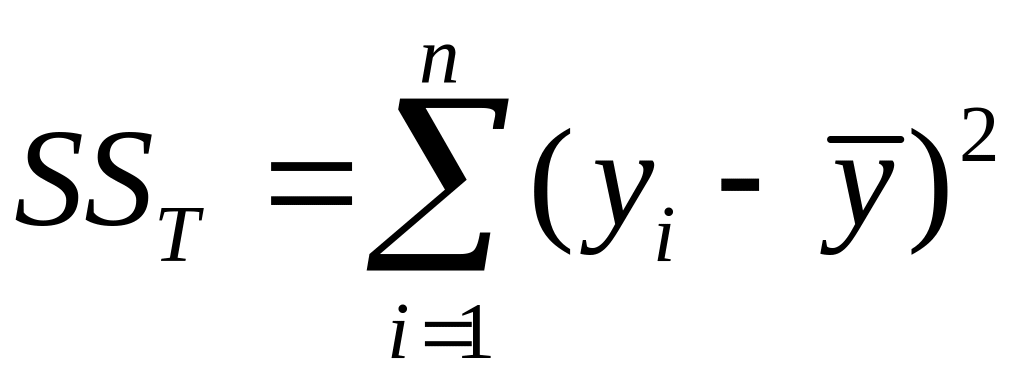Свойства мнк-оценок

а) b_i - линейная функция от наблюдений y_i , i=1-n;

b) если модель (*) верна и выполняются предположения, то b_i – наилучшие линейные оценки среди всех несмещенных оценок , т.е. имеют наименьшую дисперсию.

с) – наилучшая линейная оценка для y_i , i=1-n.

Доверительные интервалы

Заметим, что наименьшая ширина доверительного интервала для неизвестного значения Y при ; при удалении от ширина интервала увеличивается, т.е. уменьшается точность предсказания Y. Многие программы простой линейной регрессии рисуют эти доверительные интервалы в виде кривых вокруг прямой наименьших квадратов.

Проверка гипотез о коэффициентах линейной регрессии

Предположение ε_i ~N(0, σ²), i=1-n.

1. H₀: все β_i =0, т.е. независимые переменные не улучшают предсказания Y по сравнению с моделью .

H₁: не все равны нулю, т.е. некоторые из независимых переменных значимо улучшают предсказание Y по сравнению с моделью .

2. H₀: β_i =0, т.е. независимая переменная X_i не улучшает предсказания Y по сравнению с моделью без X_i.

H₁: β_i ≠0. Заметим, если отбросили некоторый член модели, необходимо найти новые оценки параметров модели, т.к. оценки обычно закоррелированы.

Замечания

1. Стандартизация переменных.

2. Для проверки гипотезы об однородности дисперсий, σ²_i= σ², используется критерий Бартлетта.

3. Для проверки гипотезы о коррелированности ошибок наблюдений ε_i часто вычисляется статистика Дурбина_Ватсона.

4. Для проверки выполнения предпосылок используется графический анализ остатков.

Множественный и частный коэффициенты корреляций

Рассмотрим ситуацию пассивного эксперимента, т. е. предположим, что матрица экспериментальных данных в этом случае является случайной выборкой значений многомерной случайной величины .

Определение. Множественным коэффициентом корреляции (multiple correlation coefficient) между и называется число , равное максимальному значению коэффициента корреляции между и любой невырожденной линейной комбинацией .

Частным коэффициентом корреляции (partial correlation) между и при фиксированных значениях переменных (список не содержит переменную ) называется число

Множественный коэффициент корреляции служит мерой линейности зависимости между и набором переменных , a частный коэффициент корреляции есть мера линейности зависимости между и , когда фиксированы.

Заметим также, что квадрат множественного коэффициента корреляции равен доле дисперсии , «объясненной» линейной регрессионной зависимостью с .

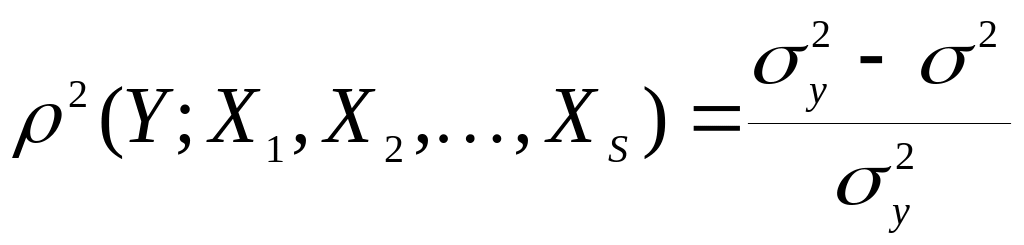
В случае простой линейной регрессии квадрат коэффициента корреляции равен доле дисперсии , «объясненной» линейной регрессионной зависимостью с (так как при m=1 множественный коэффициент корреляции есть модуль простого коэффициента корреляции).

Аналогично можно показать, что квадрат частного коэффициента корреляции можно понимать как долю остаточной дисперсии , «объясненной» добавлением к набору .

Рассмотрим теперь проверку гипотезы о том, что множественный коэффициент корреляции значимо не отличается от нуля, что эквивалентно гипотезе о том, что независимые переменные значимо не улучшают предсказания по сравнению с моделью .

Таким образом, рассмотрим (выбрав уровень значимости критерия ) следующие нулевую и альтернативную гипотезы

,

.

Естественно, статистикой критерия служит статистика (3.5)

,

которая при условии, что верна гипотеза имеет -распределение с и степенями свободы. Эта статистика вычисляется программами множественной линейной регрессии большинства ПСП в таблице дисперсионного анализа для модели множественной линейной регрессии (см. таблицу) вместе с соответствующим Р-значением.

Иначе надо построить множество принятия нулевой гипотезы, которое в данном случае имеет вид , где — квантиль -распределения с и степенями свободы порядка . И если вычисленное по выборке значение статистики критерия примет значение из множеств принятия нулевой гипотезы, то мы считаем, что гипотеза согласуется с экспериментальными данными. Иначе считаем, что гипотеза не согласуется с экспериментальными данными.

В случае простой линейной регрессии статистика критерия (3.5) служит для проверки гипотезы

,

при альтернативе

.

где - простой коэффициент корреляции и . При условии, что верна гипотеза , эта статистика имеет -распределение с 1 и степенями свободы.

С помощью статистики (3.6) проверяются гипотезы о частных коэффициентах корреляции.

Рис. 1. Прямая наименьших квадратов простой линейной регрессии. Графическая иллюстрация к определению сумм квадратов таблицы дисперсионного анализа

Таблица 3.1. Таблица дисперсионного анализа для модели множественной линейной регрессии

Источник дисперсии	Источник дисперсии	Степени свободы	Средний квадрат	F-отношение	р-значение
Регрессия
Отклонение от регрессии (остатки)
Полная

8