Регрессионный анализ

Одними из самых распространенных методов анализа связи между количественными переменными являются методы регрессионного анализа. В регрессионном анализе наиболее явно виден функциональный характер модели анализа данных. Задача регрессионного анализа – это задача поиска функциональной зависимости Y от X. Наиболее широко применяется модель множественного линейного регрессионного анализа.

Пусть в эксперименте наблюдаются значения переменной . Рассмотрим матрицу экспериментальных данных

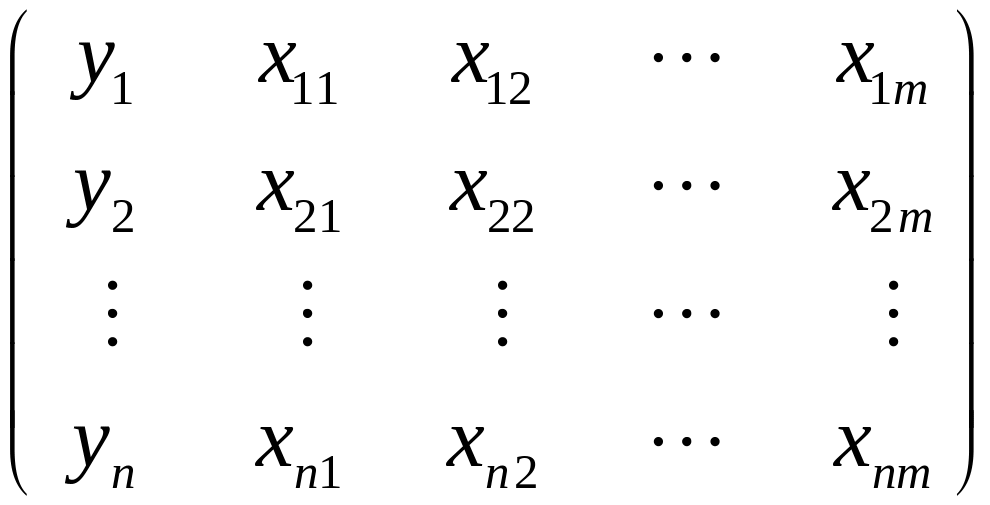
где и — значения переменных и , соответственно,

в i-м эксперименте.

В регрессионном анализе (regression analysis) рассматривается связь между переменной , называемой зависимой переменной (dependent variable), и переменными , называемыми независимыми переменными (independent variables) (слово «независимые» здесь применяется не в вероятностном смысле). Эта связь представляется математической моделью

где — неизвестные параметры, а ε — случайное отклонение Y от функции регрессии f.

Вид модели должен быть задан. Выбор модели основан:

а) на знании механизма явления;

b) на аппроксимации функции регрессии f некоторой простой функцией, которую можно рассматривать как разложение f в ряд Тейлора в небольшой окрестности изменения независимых переменных (использовать диаграммы рассеяния).

Если функция регрессии f линейна по параметрам (но не обязательно линейна по независимым переменным), то эта модель называется моделью линейного регрессионного анализа (примеры моделей, которые сводятся к линейным).

Во многих реальных задачах более подходящей является модель нелинейного регрессионного анализа (функция регрессии f не линейна по параметрам).

Два способа получения данных:

а) активный эксперимент: значения независимых переменных выбираются и устанавливаются без погрешностей экспериментатором в каждом опыте (примеры: температура, сорт…); тогда только Y является случайной величиной;

b) пассивный эксперимент: одновременно наблюдаются значения всех переменных Y, X₁, …, X_m , все эти переменные случайны, т. е. матрица экспериментальных данных в этом случае есть случайная выборка значений многомерной случайной величины {Y, X₁, …, X_m}. Например, в случайно выбранной пробе воды регистрируется число бактерий на 1 мл , температура водной среды , соленость и изучается влияние независимых переменных на численность бактерий в водоеме . Этот способ получения данных позволяет проводить корреляционный анализ, т. е. делать статистические выводы (оценивание, проверка гипотез) о мерах линейной зависимости между переменными. К мерам линейной зависимости относятся коэффициент корреляции, множественный коэффициент корреляции и частный коэффициент корреляции.

Далее будем рассматривать случай активного эксперимента. Можно показать, что результаты, полученные для случая активного эксперимента, применимы и для случая пассивного эксперимента.

Цели использования регрессионного анализа:

1. В практических исследованиях описание зависимости между переменными с помощью функции регрессии помогает установить наличие возможных причинных связей.

2. Если прямые измерения зависимой переменной затруднены, уравнение регрессии позволяет предсказать ее значения по значениям независимых переменных.

Статистические проблемы регрессионного анализа:

1. Получение наилучших точечных и интервальных оценок b_i и y_i, i=1,…,n;

2. Проверка гипотез относительно этих параметров;

3. Проверка адекватности регрессионной модели; под адекватностью подразумевается, что никакая другая модель не даст значимого улучшения в предсказании Y;

4. Проверка выполнения предположений.