Зависимость уровня издержек и прибыли от выполнения бизнес-плана по однотипным предприятиям общественного питания

Группа предприятий по степени выполнения бизнес-плана по товарообороту, %	Количество предприятий в группе	Выполнение плана товарооборота по группам предприятия, %	Уровень издержек, % к товарообороту	Уровень прибыли (рентабельности), % к товарообороту
До 100	7	93,4	20,1	0,82
100-103	8	101,8	19,8	4,10
103 и выше	9	103,9	19,6	4,20
В целом по одноти пным предприятиям	24	100,7	19,8	2,70

Применяя агрегатную форму индекса и соблюдая уста­новленную вычислительную процедуру, можно решить клас­сическую аналитическую задачу: определение влияния на объем произведенной или реализованной продукции факто­ра количества и фактора цен. Схема расчета при этом будет такой:

48

г де - влияние количества;

- влияние цен

Здесь следует напомнить, что агрегатный индекс является основной формой всякого общего индекса; его можно преоб­разовать как в средний арифметический, так и в средний гармонический индексы.

Динамика оборота по реализации промышленной продук­ции должна характеризоваться, как известно, временными ря­дами, построенными за ряд истекших лет с учетом изменения цен (это относится, естественно, к заготовительному, оптово­му и розничному оборотам).

Индекс объема реализации (товарооборота), взятый в це­нах соответствующих лет, имеет вид:

Как указывалось выше, этот индекс отражает изменение количества и цен. Поэтому обязательное условие при постро­ении рядов динамики - выражение оборота в одинаковых ценах (в ценах базисного периода), т. е. расчет индекса физи­ческого объема товарооборота по формуле

Такой пересчет товарооборота в сопоставимые цены по схеме агрегатного индекса может быть проведен, если товары (сырье, готовая продукция) учитываются не только по сумме, но и по количеству. Если количественный учет не ведется, то индекс физического объема определяется отношением индекса оборота в действующих ценах и индекса цен, исчисленного по схеме среднего гармонического индекса:

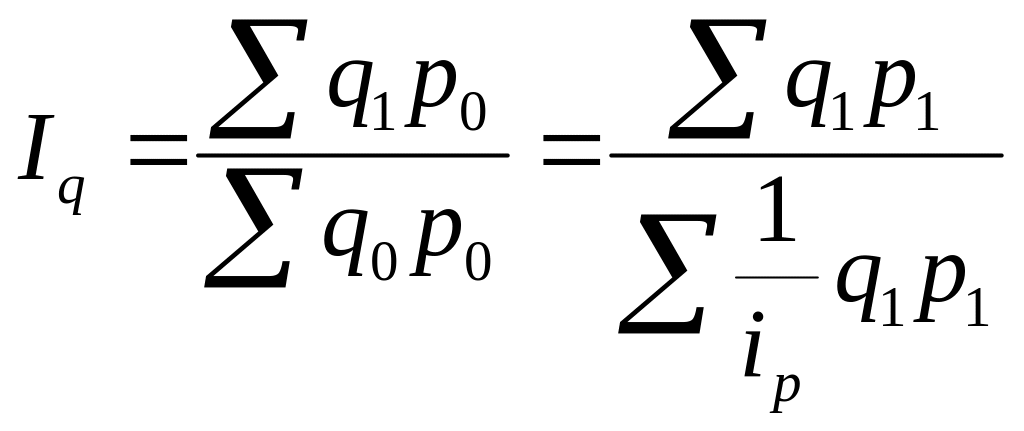
где

49

Приведенный пример наглядно иллюстрирует преобразо­вание агрегатного индекса в средний гармонический.

Использовав индексные пересчеты и построив временной ряд, характеризующий, например, выпуск промышленной про­дукции в стоимостном измерении, объем оптового или рознич­ного товарооборота (в ценах базисного периода), можно ква­лифицированно проанализировать явления динамики.

Математическая трактовка и математическая формализа­ция индексного метода приводятся в гл. 5.

Метод цепных подстановок используется для исчисления влияния отдельных факторов на соответствующий совокупный показатель. Цепная подстановка широко применяется при ана­лизе показателей отдельных предприятий и объединений. Дан­ный способ анализа используется лишь тогда, когда зависи­мость между изучаемыми явлениями имеет строго функци­ональный характер, когда она представляется в виде прямой или обратно пропорциональной зависимости. В этих случаях анализируемый совокупный показатель как функция несколь­ких переменных должен быть изображен в виде алгебраичес­кой суммы, произведения или частного от деления одних показателей на другие.

Метод цепных подстановок состоит в последовательной замене плановой величины одного из алгебраических слага­емых, одного из сомножителей фактической его величиной, все остальные показатели при этом считаются неизменными. Сле­довательно, каждая подстановка связана с отдельным расче­том: чем больше показателей в расчетной формуле, тем боль­ше и расчетов.

Степень влияния того или иного показателя выявляется последовательным вычитанием: из второго расчета вычитает­ся первый, из третьего - второй и т. д. В первом расчете все величины плановые, в последнем - фактические. Отсюда вы­текает правило, заключающееся в том, что число расчетов на единицу больше, чем число показателей расчетной формулы. При определении влияния двух факторов (двух показателей) делают три расчета, трех факторов - четыре расчета, четырех факторов - пять расчетов. Однако поскольку первый расчет включает лишь плановые величины, то его результаты можно взять в готовом виде из плана предприятия или объединения; результат последнего расчета, когда все показатели фактичес­кие, - из квартального или годового отчета. Следовательно, практически число расчетов оказывается не на единицу боль­ше, а на единицу меньше, т. е. осуществляются лишь промежу­точные расчеты.

Вычислительную процедуру с использованием метода цеп­ных подстановок покажем на конкретном примере. Допустим, требуется определить влияние на объем промышленной про­дукции трудовых факторов. Объем промышленного производ­ства может здесь приниматься

50

в виде валовой, товарной, реализованной или чистой продукции. Зависимость объема продукции от трудовых факторов математически формализу­ется так:

N^в= RТ^д Т^ч D^ч,

где N^в -объем выпуска продукции;

R - среднесписочное число рабочих;

Т^д- среднее число дней, отработанных одним рабочим за год;

Т^ч - среднее число часов, отработанных одним рабочим за день;

D^ч -средняя выработка продукции на один отработанный чело­

Показатели	План	Фактически
Объем продукции (по стоимости)1 Среднесписочное число рабочих, чел. Среднее число дней, отработанных од- ним рабочим в год Среднее число часов, отработанных од- ним рабочим в день Средняя выработка продукции на один от- работанный человеко-час (по стоимости)	2803,8 900 301 6,9 1,50	3155,2 1000 290 6,8 1,60