6.7 Матричные методы анализа

Матричные методы анализа, основанные на линейной и векторно-матричной алгебре, применяются для изучения сложных и высокоразмерных структур как на отраслевом уровне, так и на уровне предприятий и их объединений.

157

Применение матричных методов покажем на следующем примере

Два цеха предприятия выпускают продукцию двух видов: первый цех – продукцию 1-го вида, второй цех – продукцию 2-го вида. Часть выпускаемой продукции идёт на внутреннее потребление, остальная является конечным продуктом. Требуется выяснить распределение между цехами продукции, идущей на внутреннее потребление (xij), и общие (валовые) объемы выпускаемой продукции (xj), если заданы параметры прямых затрат (А) и конечного продукта (уj).

Элементы матрицы прямых затрат А представляют собой коэффициенты прямых затрат продукции i-ro вида на произ­водство единицы продукции j-ro вида. В нашем примере эти коэффициенты будут такими:

Элементы вектор -столбца у определяют величину конеч­ного продукта, идущего на внешнюю реализацию:

Для определения валового (общего) выпуска продукции l-го и 2-го видов воспользуемся следующей формулой:

где Е - единичная матрица;

(E-А)^-1 -матрица полных затрат

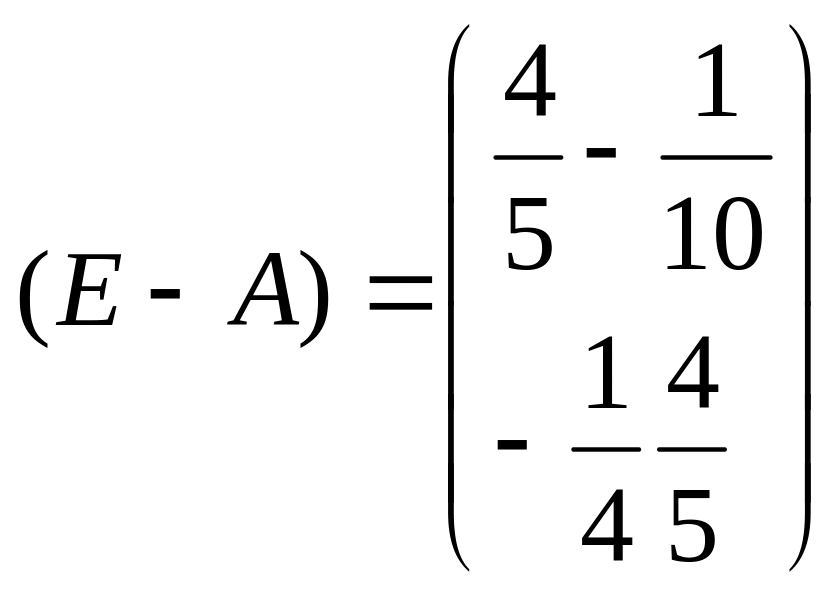
Определитель этой матрицы равен:

158

Получим обратную матрицу В = (Е-А)^-1 методом алгеб­раических дополнений.

Матрица алгебраических дополнений D формируется сле­дующим образом:

Транспонируя матрицу D и умножая на величину по­лучаем матрицу полных затрат:

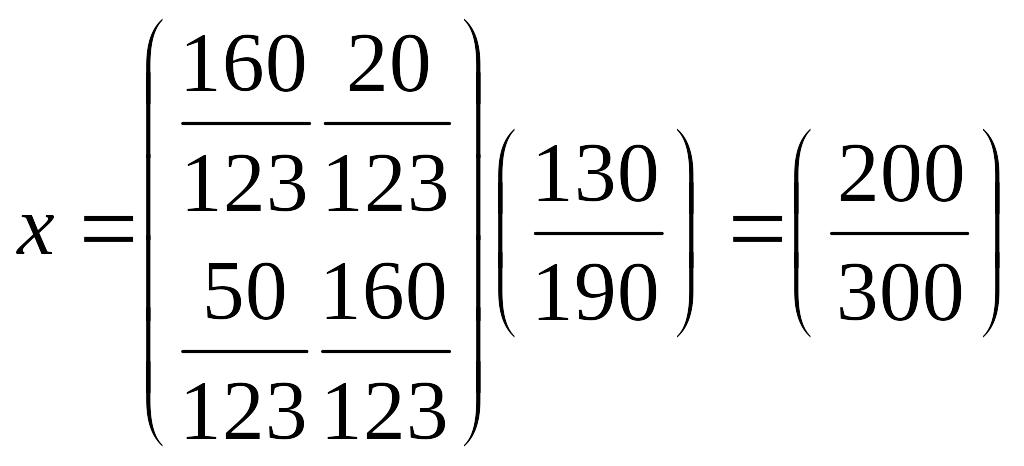
Таким образом, валовой выпуск продукции первого цеха составляет 200, а второго цеха - 300.

Распределение продукции между цехами на внутреннее по­требление определяется по формуле

В итоге плановая модель (матрица) выпуска продукции (валового и конечного продукта) с учетом внутреннего потреб­ления будет иметь такой вид (табло 6.16).

Таблица 6.16

Продукция Цех	Внутреннее потребление		Конечный I продукт	Валовой выпуск
	1	11
1	40	30	130	200
11	50	60	190	300

159

Как показывают предшествующие главы, математические методы анализа, математическое программирование и моде­лирование связаны с достаточно трудоемкими вычислитель­ными процедурами.

Специалисты считают, что выбор оптимального варианта из тысячи альтернативных, если он определяется вручную, потребовал бы времени, равного человеческой жизни долгожи­теля. Расчеты сейчас намного облегчаются применением быст­родействующей вычислительной техники. Но тем не менее глубокий и комплексный экономический анализ - дело весьма трудоемкое.

Перефразируя блестящее метафорическое определение по­эзии В. Маяковским, можно сказать, что:

Экономический анализ ­

та же добыча радия,

В грамм добыча, в год труды.

Изводишь единого показателя ради,

Тысячи тонн цифровой руды.

6.8. ТЕОРИЯ НЕЧЕТКИХ МНОЖЕСТВ'

Математическая теория нечетких множеств, созданная о 60-е гг. для решения узкой утилитарной задачи распознавания образов, в настоящее время имеет приложения в самых раз­

личных областях научной и хозяйственной деятельности – от работ по созданию искусственного интеллекта в ЭВМ пятого поколения до управления сложными технологическими про­цессами.

В основе данной теории лежат понятия нечеткого множест­ва и функции принадлежности, определение которых приводятся ниже.

Пусть Е - множество, счетное или нет, и Х - элемент Е. Тогда нечеткое подмножество А множества Е определяется как множество упорядоченных пар где А (х) - характеристическая функция принадлежности, прини­мающая свои значения во вполне упорядоченном множестве М, указывающая степень принадлежности элемента Х подмножеству А. Множеств().М называется множеством принадлеж­ностей.

Применение теории нечетких множеств в экономике ,проил­люстрируем на примере вычисления перспективного ассорти­мента оптового предприятия в одном товарном профиле при фиксированной торговой зоне. Под перспективным ассортиментом в данном случае понимается набор товаров, которые заведомо будут иметь спрос среди потребителей - в данном случае розничных торговых предприятий, входящих в район

160

эффективной коммерческой деятельности оптовой организа­ции. Нахождение перспективного ассортимента гарантирует оптовой организации формирование ассортиментного ядра, которое будет реализовано на рынке с минимальным риском, а также помогает отразить общие тенденции того потреби­тельского рынка, на котором организация оптовой торговли осуществляет свою коммерческую деятельность.

Успешное решение задачи нахождения перспективного ас­сортимента позволяет принять решение о заключении сделки при анализе поступающего коммерческого предложения.

Дано:

Х = {X1, Х2, . . . , Хп} - множество товаров, имеющихся на скла­де оптового торгового предприятия или выдвигаемых в каче­стве коммерческих предложений.

у = {y1,У2,..., Ур} - множество признаков товаров.

Z = {Z1,,Z2….. Zm} - множество рассматриваемых розничных торговых предприятии - потребителей оптовой организации.

Требуется определить перспективный ассортимент органи­зации оптовой торговли, т .е. набор Xj для удовлетворения

предполагаемых запросов из Z.

Модель строится при следующих допущениях:

1) на рынке действуют поставщик и потребители - соот­ветственно оптовая и розничные торговые организации;

2) коммерческие запросы от розничных торговых органи­заций Z 1, Z2….. Zm рассматриваются и по возможности удов­летворяются независимо от времени их поступления.

3) сделки между оптовой и розничными торговыми ор­ганизациями имеют различный порядок, который определяет­ся весовой функцией розничных организаций с помощью экспертной оценки по итогам предыдущей коммерческой деятель­ности;

4) товары Х1, Х2;..., Хn характеризуются р признаками;

5) степени принадлежности признаков У1, У2….Ур товарам

варьируются между отдельными товарами Х1, Х2…..Хт;;

6) один товар предпочитается другому всякий раз: когда его признаки уi по степени важности более близки к оценке потребителя Z {розничного предприятия).

П усть -> [О, 1] - функция принадлежности не­ четкого бинарного отношения R, определяемая с помощью эксперта.

В такой матрице элементы каждой строки выражают от­носительные степени принадлежности признаков определен­ным товарам. Чем выше значения, тем более важен признак.

Пусть Фs:У * Z -> [О, 1]- функция принадлежности не­четкого

161

бинарного отношения S. для всех У е: у и всех Z е: Z Фs(у, z) равна степени совместимости розничного торгового предприятия Z с признаком у. Чем выше значения, функции, тем более данный признак совместим с конкретным предпри­ятием розничной торговли.

Значение матрицы S отражают относительные степени важ­ности признаков У; при принятии предприятием Zj решения о закупке партии какого-либо товара у рассматриваемого нами оптовика.

Из матрицы R и S можно получить матрицу Т, элементы которой определяются функцией принадлежности.

Сумма равна степени нечеткого подмножества,

указывающей число важнейших признаков У, которое присуще

товару Х с точки зрения предприятия розничной торговли.

Далее строится матрица:

где конъюнкция означает операцию попарного минимума.

Порог разделения 1 ассортимента ограничивается условием

После того как порог 1 выбран, можно для любого Z опре­делить уровневое множество:

П усть ( (х) - весовая функция, задающая для каждого розничного торгового предприятия его вес по итогам преды­дущей коммерческой деятельности.

Ассортимент предприятия оптовой торговли описывается объединением уровневых множеств:

Вычисление перспективного ассортимента помогает опто­вому торговому предприятию определить:

162

как оптимизировать товарный ассортимент (какие товары обязательно следует иметь на складе при сохранении сложив­шейся структуры потребителей);

как изменить ассортиментную концепцию при заданном изменении зоны обслуживания, т.е. какие стратегические дей­ствия предпринять в случае выхода из числа обслуживаемых потребителей отдельных розничных организаций;

как оптимизировать зону обслуживания (в нашем случае это район эффективной коммерческой деятельности) при ис­ключении из ассортимента тех товаров, признаки которых неудовлетворяют оптовую организацию, или включении тех то­варов, признаки которых устраивают ее).

В качестве иллюстрации к данной задаче рассмотрим упро­щенный числовой пример.

Пусть оптовая организация имеет на складе потреби­тельских товаров {x₁, х2,..., х6} и осуществляет поставки трем

потребителям – Z1 в крупный универмаг), Z2 (небольшой мага­зин) и Zз (палатка).

В качестве рассматриваемых признаков товаров возьмем

следующие:

у1-«цена», уз-«внешний вид»

У2-«качество», У4-«сезонность»,

у 5 ~ «ступень жизненного цикла товара».

Пусть -> [О, 1] и фs: У х Z -> [О, 1] задаются

матрицами R и S

а значения весовой функции равны:

( z1) = 30, (z2) = 20, (z3) = 15

Характеристики товаров, стоящие в матрице R, указывают, например, что товар хi - дорогой, высококачественный, внешне неброский, соответствует сезону, но несколько устарел технически (или, наоборот, только поступает на рынок и еще неизвестен покупателям).

Характеристики магазинов, стоящие в матрице S, указыва­ют, например, что второй потребитель - магазин Z₂ – стеснен в складских помещениях и поэтому предпочитает торговать товарами, соответствующими данному сезону, что следует из значения функции Фi (У4 z2) После вычисляется матрица Т.

Заранее отметим для внимательного читателя, что уже на этом этапе можно предположить, что товар х6, как следует из последней строки матрицы Т, по всей видимости, будет закуп­лен всеми тремя потребителями. Попарными сведениями получаем матрицу W.

163

На этом этапе вычислений учитывается конкуренция между

потребителями-магазинами Z1,Z2 и Zз.

Далее находятся максимальные элементы в каждом из столбцов матрицы W:

Минимальная из этих величин - 0,5. Далее в матрице т выбираем для 1 наибольшее возможное значение, которое было бы меньше 0,5 и получаем 1 ;:::::0,475. Применяя это значение в качестве порога разделения, получаем:

М₁;::::: {Х₁, , Х₂ Хз, Х4, Х5, Х6,},

М₂;::::: (Х₁ ,Хз, Х5, Х6},

М₃::::: (Х₄ ,Х6, }

Таким образом, широкие возможности крупного универма­га Z_] позволяют ему торговать всем спектром продукции, предлагаемой оптом, магазин Z_] в силу недостатка складских помещений, избегает приобретать товары, реализация кото­рых потребует длительного срока, а палатка Z3 берет только броские и относительно недорогие товары. Большой спрос на товар Х6 не случаен, это действительно товар с блестящими характеристиками: он имеет невысокую цену при среднем ка­честве, великолепно выглядит, соответствует сезону и достато­чно известен розничному покупателю.

Воспользовавшись значениями весовой функции, получаем значения accopтиментa:.

м = {50х₁, ЗОХ₂, 50хз, 45х4, 50х5, 1О5х6}

Результатами этой задачи легко воспользоваться при при­нятии решения о заключении сделки (при анализе поступающе­го коммерческого предложения).

Для этого следует, определив функцию принадлежности предлагаемого товара Х_{п +1,} провести счет согласно. приведен­ному алгоритму', и определить, в какой степени этот товар принадлежит множеству товаров перспективного ассортимен­та, а если принадлежит, то не вытеснит ли он каких-либо товаров из набора Х1, . . ., Хп, уже находящихся на складе предприятия оптовой торговли.

На основании этой оценки лицо, ответственное за заключе­ние сделки, может принять положительное, выжидательное или отрицательное решение.

164