6.6. Математическая теория массового обслуживания

Теория массового обслуживания впервые применялась в те­лефонии, а затем и в других областях хозяйственной деятель­ности.

Например, организация нормального процесса обслужива­ния покупателей связана с правильным определением следу­ющих показателей: количества предприятий данного торгового профиля, численности продавцов в них (в том числе и «механи­ческих»), наличия соответствующих основных фондов, частоты завоза товаров, численности обслуживаемого населения, плот­ности обращаемости и потребности в соответствующих товарах(по групповому и внутригрупповому ассортименту). Если пред­положить, что предприятие располагает необходимыми основ­ными фондами, торгует товарами, имеющимися в достаточном количестве (при нормальной частоте завоза), то и тогда в про­цессе обслуживания остаются такие переменные величины, ко­торые могут существенно повлиять на качество обслуживания. Надлежит, следовательно, выбрать такой оптимальный вари­ант организации торгового обслуживания населения, при кото­ром время обслуживания будет минимальным, качество высоким, не будет излишних народнохозяйственных затрат. Математический аппарат теории массового обслуживания облегчает решение этой задачи. При этом различают две формы об­служивания: с неявными потерями и с явными потерями.

Систему массового обслуживания с неявными потерями (правило очередей) можно показать на примере обслуживания рабочих необходимым инструментом (из обособленных кладо­вых промышленного предприятия Допустим, что в инструментальной кладовой работают два

кладовщика. Требуется определить, в какой мере они своевре­менно обеспечивают заявки на обслуживание, поступающие от рабочих; не обходятся ли простои рабочих в очереди за инст­рументом дороже, чем дополнительное содержание еще одно­

го или двух кладовщиков?

Для решения данной задачи необходимы прежде всего хронометражные замеры о потоке требований на обслуживание в единицу времени. Если хронометраж осуществлялся в течении 10 дней каждые 15 мин. за смену (кроме начала и конца рабочего рабочего дня), то за этот отрезок времени было произведено 300 наблюдений (30 наблюдений, умноженное на 10). Время наблюдений (1) составит 4500 мин (15*300). Причем таких промежутков, когда на склад никто не приходил или приходил только один рабочий, не наблюдалось, приход двух рабочих отмечался один раз, трех - три раза и т. д. (табл. 6.12).

Частота прихода двух рабочих при 300 наблюдениях равна

0,33 (1/300*100), трех - 1 (3/300*100) и т. д.

153

Таблица 6.12

Число приходов в единицу времени (за 15 мин)	Наблюдаемое число приходов, %	Наблюдаемая частота приходов, %	Полное число приходов рабочих (гр. 1*гр2)		Число приходов в единицу времени (за 15 мин)		Наблюдаемое число приходов, %			Наблюдаемая частота приходов, %		Полное число приходов рабочих (гр. 1*гр2)
О	О	О		О		15	23				7,67		345
1	О	О		О		16	20				6,67		320
2	1	0,33		2		17	'18				6,00		306
3	3	1,00		9		18			16		5,33		288
4	5	1,67		20		19			13		4,33		247
5	8	2,67		40		20			11		3,67		220
6	10	3,33		60		21			10		3,33		210
7	12	4,00		84		22			8		2,67		176
8	13	4,33		104		23			5		1,67		115
9	16	5,33		144		24			3		1,00		72
10	18	6,00		180		25			1		0,33		25
11	20-	6,67		220		26			1		0,33		26
12	19	6,33		228
13	21	7,00		273					300		99,99
14	25	8,33		350

Для определения среднего числа приходов в единицу време­ни (л.) исчисляется полное число приходов (М как сумма произведений числа приходов (количества пришедших в кладо­вую рабочих) на наблюдаемое число приходов.

Таким образом, среднее число требований на обслужива­ние, т. е. среднее число приходов в единицу времени (л.), со­ставит

= 4064/4500=0,903 чел.-мин.

Чтобы определить распределение вероятностей для длите­льности обслуживания при предположении, что закон распре­деления экспоненциальный, вычислим среднюю продолжите­льность одного обслуживания (Т_обсл); она равна 1,6 мин.

П осле этого можно установить интенсивность обслуживания ( )

Т_обс;= 1/Т_обсл ; = 1/1,6 = 0, 625 чел.- мин.

В случае, когда л.< , увеличения очереди не возникает, так как удовлетворение требований происходит не ранее их посту­пления. В нашем примере л. > (0,903 > 0,625) и в кладовой образуется очередь. Точно определить величину очереди как случайную нельзя. Можно вычислить вероятность того, что в момент времени (t) очередь будет характеризоваться числом требований Pn(t):

154

где Po(t) - вероятность отсутствия очереди.

В тех случаях, когда > 1, вероятность отсутствия очереди

( ₀) обычно берется из графиков (в нашем пример = 1,445).

Д ля построения таких графиков воспользуемся таблицей значений Р_О для различных значений и п (п – количество кладовщиков в инструментальной кладовой).

По данным табл. 6.13, в нашем случае рассматривается многолинейная система, когда п> 1 (количество кладовщиков превышает единицу).

Таблица 6.13

n

2

3

4

5

6

7

…..

1 0,33 0,363 0,367 0,367 0,367 0,368

2 0,111 0,130 0,134 0,135 0,135

3 0,037 0,046 0,049 0,050

4 0,013 0,016 0,018

Определим среднее время ожидания (Тс), которое склады­вается из среднего времени ожидания обслуживания в очереди (Т_ох) и среднего времени обслуживания (Т oбcл):

Тс= Т_ох + Т oбcл,

В том случае, когда в системе работает п кладовщиков, среднее время ожидания в очереди определится по формуле при п = 2:

Т_ох=1,445² *0,536/2*210,625*(1-1,445/2)=1,119/0,694 =1,613;

при п = 3

Т_ох= 1,445² *0,386/3*310,625*(1-1,445/3)=1,165/5,831=0,199;

Тс= 0,199+1,6=1,799 мин;

при п = 4

Т_ох=1,445² *0,306/4*410,625*(1-1,445/4)=1,334/38,325=0,035;

Тс=0,035+1,6=1,635 мин и т.д.

155

Предположим, что у рабочего потери от простоев состав­ляют 5, а содержание кладовщика - 4 ден. ед. в единицу времени. За период времени Т в систему поступает лТ заявок, т.е. 1,445Тзаявок.

Порядок исчисления показателя качества обслуживания с явными потерями покажем на примере для условий пpостей­шего потока требований.

Стол заказов при крупном универсаме оборудован четырь­мя телефонами. Среднее число вызовов в течение часа состав­ляет 96, среднее время, затрачиваемое на прием одного заказа, - 2 мин. Требуется определить, как полно загружены прием­щики заказов, какова вероятность отказа в обслуживании.

Степень загруженности приемщиков определяется по формуле:

По условиям примера п = 4 (4 телефона, 4 приемщика заказов), л = 96 (число вызовов в течение часа); среднее время, затрачиваемое на прием одного заказа, составляет 2 мин, или 2/60=1/30единицы времени; значение параметра r = 1 : 1/30= 30, величины вероятностей Ро,Р..Р2,Рз приведены в табл. 6.15. Значение членов второго столбца найдено по формуле

Как известно

отсюда

Умножая каждое из значений Pk/ Р_О на Р_О = 0,0522, получим величину Pk. Затем, умножая значение членов третьего столбца на значения первого столбца (на О), второго (на 1) и т.д. И суммируя их, получим математическое ожидание числа заня­тых приемщиков:

Следовательно, каждый приемщик заказов будет занят в среднем 0,62 рабочего дня ( 2,4693/4).

Ответим на второй вопрос: какова вероятность отказа в обслуживании?

156

Таблица 6.15

Величины вероятностей

Число приёмщиков		Pk/ РО	Pk		КPk
0	1,0			0,0522		О
1	3,2			0,1670		0,1670
2	5,12			0,2673		0,5346
3	5,462			0,2851		0,8553
4	4,369			0,2281		0,9124
	19,151			0,9997		2,4693

Для этого найдем вероятность того, что все приемщики будут заняты в момент обращения очередного клиента:

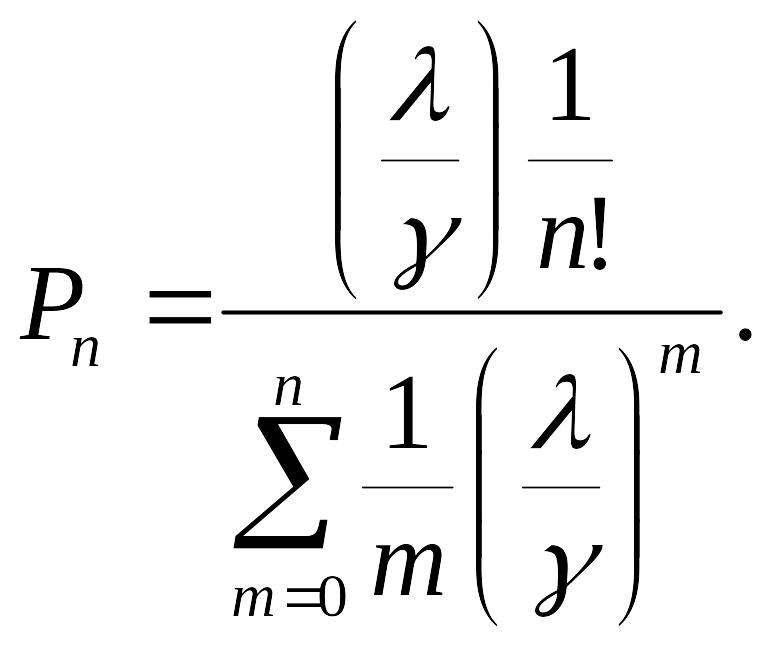
Подставляя значения = 3,2, п= 4, найдем значение Рп:

Р₄ = (3,2)² *1/41/1+3,2*(3,2) ² /2+(3,2) ³ /31+(3,2) ⁴ /41=4,369/19,151=0,23.

Полученный результат показывает, что из 100 заказчиков в среднем 77 будут обслужены, а 23 - нет. Следовательно, обслуживающую систему нельзя признать достаточной (23%отказов); экономия на численности обслуживающего аппа­рата отрицательно влияет на качество обслуживания населения.

Число приемщиков отдела заказов целесообразно увеличить до пяти, тогда математическое ожидание числа необслуженных заявок составит лишь 0,13. Иными словами, из 100 заказчиков будет обслужено 87, а 13 получат получат отказы. Таким образом, увеличение числа приемщиков на одного повысит качество обслуживания с 77 до 87%.