Мощность в цепях периодического несинусоидального тока

Пусть;

Тогда для активной мощности можно записать:

Как было показано при выводе соотношения для действующего значения несинусоидальной переменной, среднее за период значение произведения синусоидальных функций различной частоты равно нулю. Следовательно,

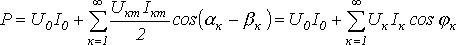
Где

Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармонических:

Аналогично для реактивной мощности можно записать

Полная мощность

где Т – мощность искажений, определяемая произведениями действующих значений разнопорядковых гармонических тока и напряжения.

Лямда(Л)=коэффициент мошьности=P/S=K_u*cosф1

К_И- коэффициент искажений

Л в цепи несинусоидального тока меньше чем в цепи синусоидального тока, т.е несинусоидальность приводит к ухудшению энергетических показателей.

Билет 18. Методика расчета линейных цепей при несинусоидальных токах

Возможность разложения периодических несинусоидальных функций в ряд Фурье позволяет свести расчет линейной цепи при воздействии на нее несинусоидальных ЭДС (или токов) источников к расчету цепей с постоянными и синусоидальными токами в отдельности для каждой гармоники. Мгновенные значения искомых токов и напряжений определяются на основе принципа наложения путем суммирования найденных при расчете гармонических составляющих напряжений и токов.

(при расчете спектр рассматриваемых гармоник ограничивается) в расчетном плане представляется суммой цепей на рис. 6.

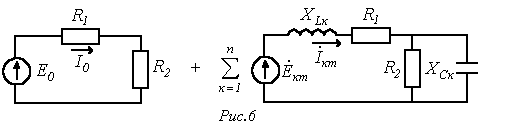
Тогда, например, для тока в ветви с источником ЭДС, имеем

Необходимо помнить, что ввиду различия частот суммировать комплексы различных гармоник недопустимо.

Таким образом, методика расчета линейных цепей при несинусоидальных токах сводится к следующему:

1. ЭДС и токи источников раскладываются в ряды Фурье.

2. Осуществляется расчет цепи в отдельности для каждой гармонической.

3. Искомые величины определяются как алгебраические суммы соответствующих гармонических.

Билет 19. Особенности протекания несинусоидальных токов через пассивные элементы цепи

Резистор.

несинусоидальные U и I совподают по форме и подобны друг другу.

Это позволяет на практике осцилографировать форму тока с помощью регистрации напряжения на шунте.

Конденсатор.

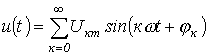
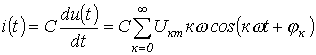
Конденсатор искажает форму кривой тока по сравнению с напряжением, являясь сглаживающим элементом для последнего.

Катушка индуктивности.

Принимая во внимание соотношение между напряжением и током для катушки индуктивности

совершенно аналогично можно показать, что в случае индуктивного элемента , т.е. кривая напряжения искажена больше, чем кривая тока. Этому случаю будет соответствовать рис. 5 при взаимной замене на нем кривых напряжения и тока. Таким образом, катушка индуктивности является сглаживающим элементом для тока. С учетом вышесказанного на практике, например в силовой полупроводниковой технике, для сглаживания выпрямленного напряжения применяют конденсаторные фильтры, а для тока – дроссели.