6. Введем параметры для решения задачи линейного программирования.

• В диалоговом окне поместить указатель мышки на кнопку Параметры. На экране появится диалоговое окно Параметры поиска решения (рис. 10).

• Установить флажки в окнах Линейная модель (это обеспечит применение симплекс-метода), Неотрицательные значения, МетодНьютона.

Рис. 10. Ввод параметров

• Поместить указатель мыши на кнопку ОК. На экране появится диалоговое окно Поиск решения.

• Поместить указатель мыши на кнопку Выполнить.

Через непродолжительное время появятся диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками B3:D3 для значений х_i,. и ячейка F4 с максимальным значением целевой функции 15 (рис. 11).

Рис. 11. Диалоговое окно Результаты поиска решения и результат решения задачи

В результате решения задачи был получен ответ: для выполнения ассортиментного набора с минимальными затратами необходимо добавлять на 1000 л топлива 10 л продукта А, а продукт В – не использовать совсем. При этом минимальные затраты составят 15 ф.ст., и все заданные ограничения по ресурсам в оптимальном плане будут соблюдены.

Задача 2. Оптимальный план перевозок грузов.

Три завода (А, В и С) поставляют некоторую разновидность стали на пять торговых складов. Спрос каждого торгового склада в декабре, наличие стали на заводах, а также значения стоимости транспортировки 1 т стали приведены в следующей таблице.

Завод	Предложение, т	Транспортные издержки, ф.ст. за единицу Торговый склад
		1	2	3	4	5
А	200	20	27	33	25	34
В	250	22	36	34	28	26
С	300	26	29	27	26	28
Потребность, т		100	150	200	100	200

Требуется определить минимальную стоимость перевозки за декабрь.

Обозначим запасы груза на заводах как a_i , а потребности складов как b_j. В данном случае суммарные запасы (200+250+300 = 750) равны суммарным потребностям (100+150+200+100+200 = 750). Такая транспортная задача называется закрытой. В таблице условия задачи даны удельные расходы на перевозку. Это т.н. матрица перевозок. Значения удельных расходов обозначим как c_ij, где i – строка поставщика, а j – столбец потребителя. Количество единиц груза, которое нужно перевезти от i-го поставщика к j-му потребителю обозначим как x_ij. Целевая функция задачи представляет собой сумму расходов на перевозку всех запасов ко всем потребителям и имеет вид:

m – число поставщиков;

n – число потребителей.

Условия «все грузы должны быть перевезены» и «все потребности должны быть удовлетворены» выразятся следующими формулами:

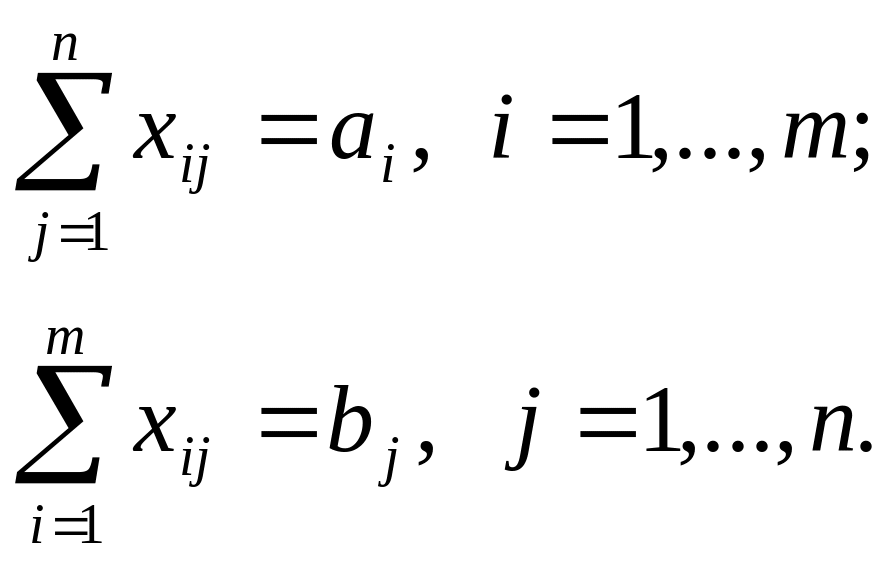
Исходя из этого, математическая модель транспортной задачи имеет вид:

Найти минимальное значение линейной функции

при ограничениях:

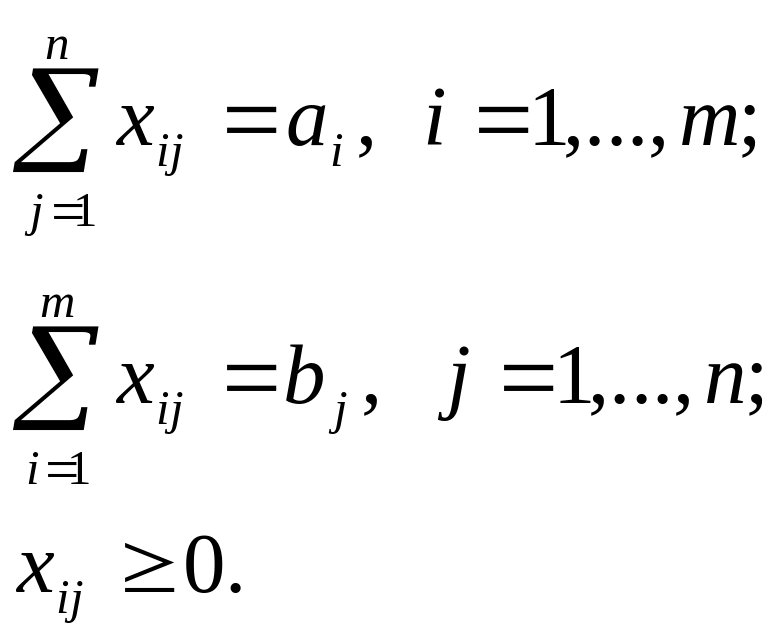
Решение задачи с помощью ПП MS Excel состоит из следующих шагов.