Лекція №4 Тема лекції: «Заміна змінних у подвійному інтегралі»
1. Поняття про регулярні відображення. Площі фігур при регулярних відображеннях.
2. Заміна змінних у подвійному інтегралі.
3. Подвійний інтеграл у полярних координатах.
Поняття про регулярні відображення.
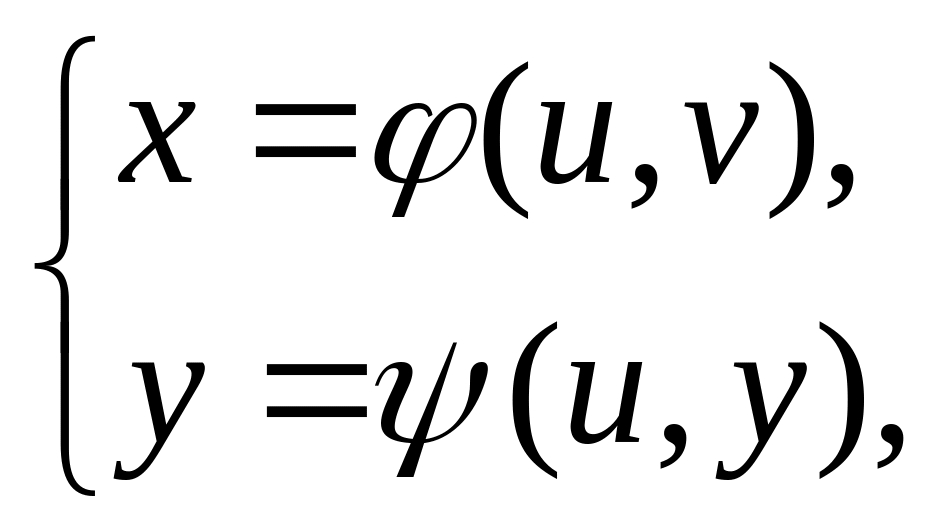(4.1)
що
визначені на множині
координатної площини
,
а відповідні їх значення є координатами
точок
,
які утворюють множину
координатної площини
,
тобто функції (4.1) відображують множину
у множину
.
Означення. Відображення (4.1) називається регулярним відображенням множини у множину , якщо виконуються такі умови:
1)
функції (4.1) бієктивно відображують
множину
з межею
на множину
з межею
;
2)
частинні похідні
неперервні
на множині
3) визначник
(4.2)
який називається якобіаном або визначником Якобі, не дорівнює нулю на множині .
Відомо,
що регулярні відображення перетворюють
квадровні множини у квадровні множини.
При цьому площа множини
обчислюється за формулою
.
(4.3)
Оскільки
модуль якобіана є неперервною функцією
на множині
,
то за теоремою 2.2 про середнє значення
подвійного інтеграла існує точка
така, що
.
На наступному прикладі розглянемо як регулярні відображення змінюють межу і площу множини.
Приклад.
Знайти образ
прямокутника
при
відображенні
і встановити залежність між їх площами.
Р
о з в’я з а н н я. Нехай
– вершини прямокутника – мал. 4. Знайдемо
образи сторін.
– верхня
половина кола;
– верхня
половина кола;
відрізок
осі
;
відрізок
осі
.
Побудувавши
дуги кіл і відрізки, дістанемо верхню
половину кільця
(мал. 5), яка є образом прямокутника
.
Мал. 4 Мал. 5
Обчислимо
площу прямокутника
і площу кільця
:
.
Обчислимо площу множини , використовуючи формулу 4.3. Для цього знайдемо якобіан:
і
обчислимо
,
використовуючи подвійний інтеграл:
.
Результати обчислень, отримані різними способами, узгоджуються. При цьому
– коефіцієнт
зміни площі.
Заміна змінних у подвійному інтегралі. Нехай маємо подвійний інтеграл
,
у якому підінтегральна функція неперервна в області інтегрування, і регулярне відображення
деякої множини у множину .
Встановимо
формулу, яка дозволить у подвійному
інтегралі від змінних
перейти до змінних
.
Для цього виконаємо
-розбиття
множини
прямими, паралельними координатним
осям
і
– мал. 6а.
Лінії, що є образами цих прямих при
відображенні (4.1), виконають
-розбиття
множини
– мал. 6б.
При цьому замкнені прямокутники
,
що утворюють
-розбиття
множини
,
перетворяться у замкнені криволінійні
чотирикутники
,
що виконують
-розбиття
множини
.
Їх площі пов’язані співвідношеннями
,
де
.
Побудуємо інтегральну суму для функції
,
що відповідає
-розбиттю
множини
:
,
де
.
Маємо
.
а б
Мал. 6
У
правій частині отриманої рівності
міститься інтегральна сума для неперервної
на множині
функції
,
що відповідає
-розбиттю
цієї множини. Якщо
– найбільший діаметр множин
,
а
– найбільший діаметр множин
,
то можна довести, що вони одночасно
прямують до нуля. Тому з рівності
дістаємо рівність
,
(4.4)
яка називається формулою заміни змінних у подвійному інтегралі.
Подвійний
інтеграл у полярних координатах. Полярні
координати
точки пов’язані з декартовими координатами
цієї точки рівностями
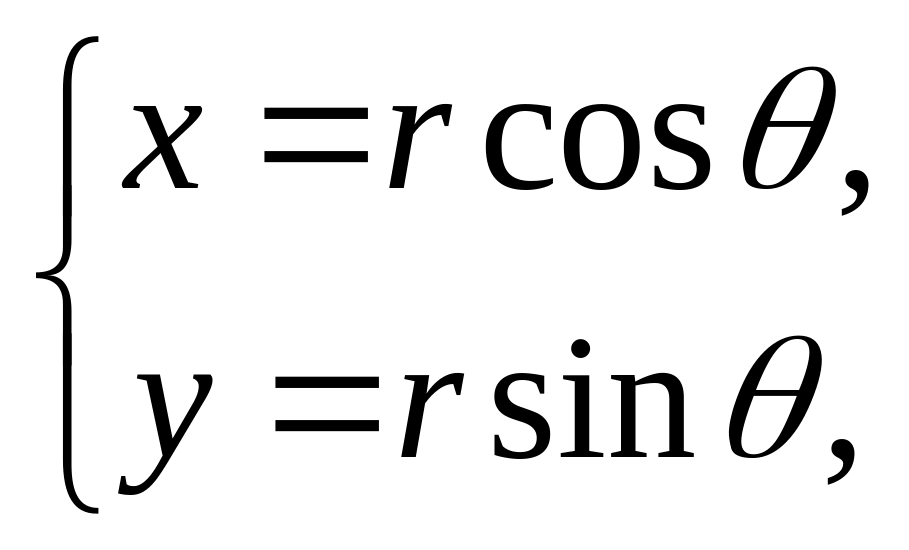
де
– додатне число,
.
Ці рівності задають регулярне відображення
декартової координатної площини
в декартову координатну площину
.
Оскільки
,
то перехід від декартових координат до
полярних координат у подвійному інтегралу
здійснюється за формулою
.
Приклад 1. Обчислити подвійний інтеграл
по
області
Р
о з в’я з а н н я. Область
– верхня половина круга радіуса
з центром в початку координат. Нехай
– довільна точка області
,
– її полярні координати. Тоді
.
Використовуючи формулу переходу (4.4),
дістанемо
.
Відповідь:
.
Приклад
2. У подвійному інтегралі
,
де
,
перейти до полярних координат.
Р
о з в’я з а н н я.
Областю інтегрування є круг радіуса
з центром в точці
.
Для розв’язання задачі потрібно
визначити межі зміни полярних координат.
Нехай
– горизонтальний діаметр кола, яке
обмежує область
,
– довільна точка цього кола,
.
Оскільки трикутник
прямокутний, то
.
Якщо
– довільна точка відрізка
і
– її полярні координати, то
.
Використовуючи формулу переходу (4.4), дістанемо
.
Примітка. У подвійному інтегралі переходити до полярних координат доцільно тоді, коли областю інтегрування є круг або частина круга.