ВОРОНИЙ О.М.

МАТЕМАТИЧНИЙ АНАЛІЗ

ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ КІЛЬКОХ ЗМІННИХ

Лекції для студентів другого курсу спец. «Математика»

IV семестр, 2014 – 15 н.р.

КРАТНІ ІНТЕГРАЛИ

ПОДВІЙНІ ІНТЕГРАЛИ

Лекція №1

Тема лекції: «Квадровні множини»

1. Квадровні множини та їх площі.

2. Критерій квадровності.

Квадровні множини та їх площі. Нехай – деяка множина точок площини, – довільні многокутні фігури цієї площини (многокутники або скінченне об’єднання многокутників) такі, що

.

Введемо позначення: – площі многокутників. За властивістю площ многокутних фігур . Тому множина – обмежена зверху, – обмежена знизу. За теоремою про існування граней обмежених числових множин множина має верхню грань, яку позначимо , множина – має нижню грань, яку позначимо .

Означення. Невід’ємні числа

(1.1)

(1.2)

називаються внутрішньою і зовнішньою площами множини відповідно.

Означення. Якщо внутрішня і зовнішня площі множини однакові, то множина називається квадровною, а спільне значення її внутрішньої і зовнішньої площ називається площею множини і позначається :

. (1.3)

Зауваження. Якщо множина не містить внутрішніх точок, то вважають, що внутрішня площа такої множини дорівнює нулю.

Критерій квадровності. Множина квадровна тоді й тільки тоді, коли для будь-якого додатного числа існують многокутні фігури такі, що , для площ яких виконується нерівність

. (1.4)

Д о в е д е н н я. Необхідність. Нехай – квадровна множина: виконується рівність (1.3). Тоді з рівностей (1.1) і (1.2) за властивостями нижньої грані маємо

(1.5)

а за властивостями верхньої грані:

(1.6)

Використовуючи другі нерівності цих систем дістаємо нерівність

.

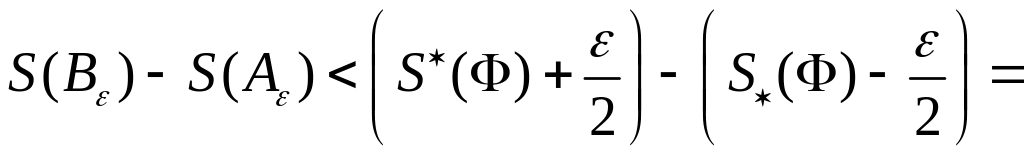
Необхідність доведено.

Достатність. Нехай виконується умова (1.4). Тоді перші нерівності систем (1.5) і (1.6) виконуватимуться і для многокутників :

, (1.7)

. (1.8)

Тому

.

Одержана рівність означає, що множина – квадровна. Достатність доведено.

Означення. Кажуть, що множина має нульову площу, якщо її можна помістити у многокутну фігуру, площа якої менша за довільне додатне число .

Приклад 1.1. Довести, що скінченна множина точок площини є квадровною множиною і її площа дорівнює нулю.

Р о з в’я з а н н я. Нехай множина складається з точок . Побудуємо квадрати , сторони яких дорівнюють 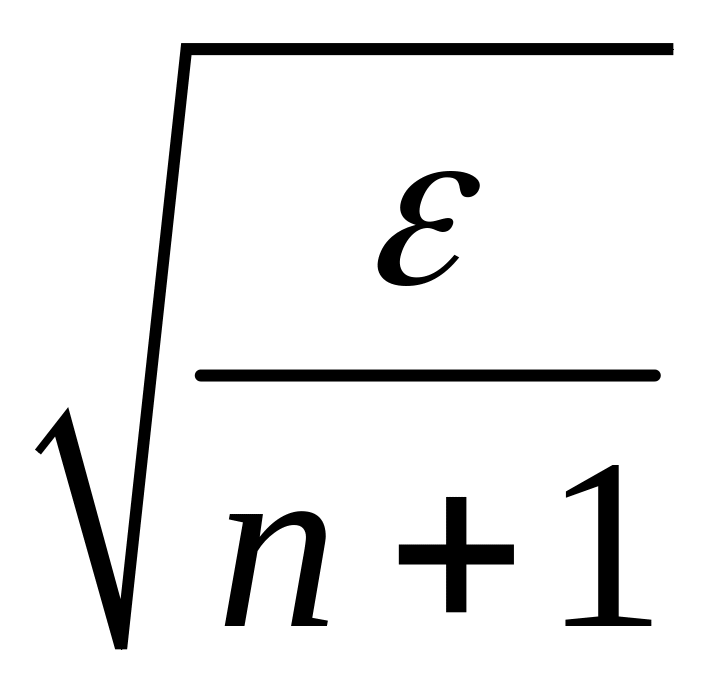, а точки є точками перетину їх діагоналей. Об’єднання є многокутною фігурою, у якій міститься множина . Оскільки

,

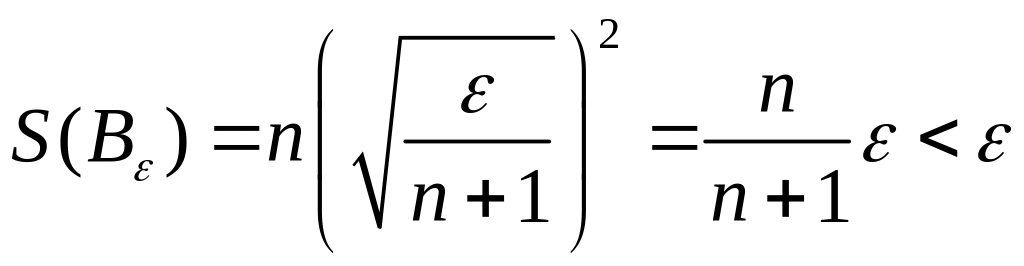то .

Приклад 1.2. Довести, що графік функції, неперервної на відрізку , має нульову площу.

Р о з в’я з а н н я. За теоремою Кантора функція – рівномірно неперервна на відрізку . Тому

.

Виконаємо Т-розбиття відрізка точками так, щоб

для . Нехай

.

На координатній площині побудуємо прямокутники і з висотами і відповідно, основами яких є геометричні відрізки . Тоді графік функції міститиметься в многокутній фігурі . Оскільки

,

то площа графіка неперервної функції дорівнює нулю.

Теорема 1.1. Якщо межа множини має нульову площу, то ця множина квадровна.

Теорема 1.2. Якщо межа множини є неперервною кривою, то множина квадровна.

Приклад. Криволінійна трапеція є квадровною множиною.

Властивості квадровних множин.

1. Скінченне об’єднання квадровних множин є квадровною множиною. При цьому, якщо множини не мають спільних внутрішніх точок, то площа їх об’єднання дорівнює сумі площ цих множин.

2. Перетин квадровних множин є квадровною множиною.

Лекція №2 Тема лекції: «Подвійний інтеграл»

1. Означення подвійного інтеграла.

2. Суми Дарбу та їх властивості.

3. Критерій інтегровності функції двох змінних.

4. Інтегровність неперервної функції.

5. Основні властивості подвійного інтеграла.

Означення подвійного інтеграла. Нехай – замкнена квадровна множина координатної площини . Кажуть, що квадровні замкнені множини виконують - розбиття множини , якщо:

1.

2. попарно не мають спільних внутрішніх точок;

3. .

Діаметром множини називається найбільша відстань між її точками.

Задамо на множині обмежену функцію і виконаємо - розбиття цієї множини множинами .

Означення. Сума , де , – площа множини , називається інтегральною сумою Рімана для функції , що відповідає - розбиттю множини , і позначається символом :

.

Означення. Число І називається границею інтегральної суми за умови, що , де – найбільший з діаметрів множин , якщо для довільного числа існує додатне число таке, що з умови виконується нерівність

.

При цьому використовують позначення

.

Означення. Якщо існує скінченна границя інтегральної суми функції , яка відповідає - розбиттю множини , за умови, що , то функція називається інтегрованою за Ріманом на множині , а границя називається подвійним інтегралом функції по множині і позначається символом

.

Змінні називаються змінними інтегрування, – підінтегральна функція, – підінтегральний вираз, – область інтегрування. Отже, за означенням

.

Суми Дарбу. Якщо функція обмежена на множині , то вона також обмежена на кожній з множин , що виконують її -розбиття. Тому на цих множинах існують грані множини її значень, які позначимо так:

Означення. Суми 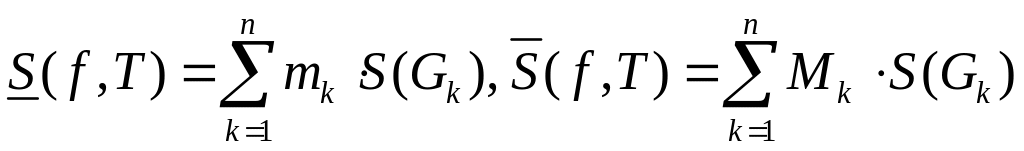називаються нижньою і верхньою сумами Дарбу функції , що відповідають - розбиттю множини .

Величина інтегральної суми залежить від - розбиття множини і від вибору точок на цих множинах. Якщо - розбиття зафіксоване, то інтегральна сума залежить тільки від вибору точок . Нескладно довести, що нижня сума Дарбу, яка відповідає - розбиттю є нижньою гранню множини інтегральних сум, що відповідає цьому ж розбиттю, а верхня сума Дарбу, яка відповідає - розбиттю, є верхньою гранню множини інтегральних сум, що відповідає цьому ж розбиттю:

.

Властивості сум Дарбу. Якщо виконати розбиття хоч би однієї з множин , що виконують - розбиття множини , то утвориться нове - розбиття цієї множини, яке називається продовженням - розбиття множини .

1. При продовженні - розбиття множини нижня сума Дарбу функції не спадає, а верхня сума Дарбу – не зростає:

.

2. Для довільних і розбиттів множини нижня сума Дарбу, що відповідає - розбиттю, не більша за верхню суму Дарбу, що відповідає - розбиттю:

.

З другої властивості випливає, що множина нижніх сум Дарбу, які залежать від розбиття множини обмежена зверху, а множина верхніх сум Дарбу – обмежена знизу. Тому існують грані множин цих сум:

.

Числа називаються нижнім і верхнім інтегралами Дарбу відповідно.

Критерій інтегровності функції двох змінних. Для того щоб обмежена функція була інтегрованою на замкненій квадровні множині необхідно і достатньо, щоб для довільного числа існувало таке число , що нерівність

виконувалася як тільки .

Д о в е д е н н я. Необхідність. Якщо функція інтегрована, то існує скінченна границя інтегральної суми

.

За означенням границі інтегральної суми маємо, що для довільного числа існує додатне число таке, що з умови виконується нерівність

.

З нерівності випливає, що

,

а з нерівності маємо

.

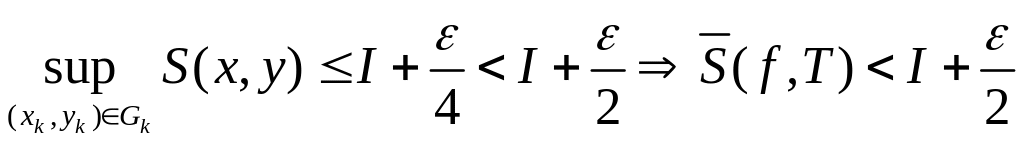Далі отримуємо

Необхідність доведено.

Достатність. З означень нижнього і верхнього інтегралів Дарбу, нижньої і верхньої граней дістаємо нерівності

.

Нерівність може виконуватися для довільного додатного тільки за умови, що . Оскільки

і

,

то

за умови, що . А це означає, що І – скінченна границя інтегральної суми функції , коли , тобто – інтегрована функція.

Достатність доведено.

Інтегровність неперервної функції. Теорема 2.1. Якщо функція неперервна на замкненій квадровній множині , то на цій множині вона інтегрована.

Д о в е д е н н я. Оскільки множина квадровна, то вона обмежена. За теоремою Кантора на обмеженій замкненій множині неперервна функція є рівномірно неперервною. Тому функція рівномірно неперервна на множині , а отже, для довільного числа існує число таке, що для всіх точок , відстань між якими менша за , відстань між відповідними значеннями функції менша за , де – площа множини :

, якщо .

Множинами виконаємо - розбиття множини так, щоб діаметр кожної з них був менший за . Утворимо суми Дарбу

,

де

За ІІ теоремою Вейєрштрасса неперервна функція на кожній обмеженій замкненій множині набуває свого найменшого і найбільшого значень, тобто існують такі точки , що . Зрозуміло, що , тому . Утворимо різницю верхньої і нижньої сум Дарбу:

Отже, , якщо . За критерієм інтегровності неперервна функція інтегрована на замкненій квадровній множині .

Теорему доведено.

Основні властивості подвійного інтеграла. Для функцій, інтегровних на замкнених обмежених множинах, мають місце такі властивості.

1.

2. Сталий множник можна виносити за знак інтеграла:

3. Інтеграл від скінченної алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів цих функцій:

.

4. Адитивна властивість. Якщо замкнені квадровні множини не мають попарно спільних внутрішніх точок і , то

.

5. Якщо для функцій і на множині виконується нерівність

,

то для інтегралів виконується аналогічна нерівність

.

Теорема 2.2 (про середнє значення). Якщо функція неперервна на квадровній замкненій множині , то існує така точка , що

де – площа множини .