ОЦЕНКА ДОСТОВЕРНОСТИ. Дорохова.

ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ

В научных исследованиях и практической деятельности сте­пень достоверности результатов измерения и расчета не ме­нее важна, чем сам результат. Любое измерение выполняется с некоторой погрешностью. Химик должен уметь оценить по­грешность получаемых результатов.

Виды погрешностей

По происхождению погрешности химического анализа клас­сифицируют на систематические и случайные.

Систематические погрешности обусловлены постоянно действующими причинами. Такие погрешности можно вы­явить, устранить или учесть при расчетах. Они постоянны во всех измерениях или изменяются с определенной закономер­ностью. Систематические погрешности имеют определенный знак.

Случайные погрешности возникают в результате некон­тролируемых изменений в условиях измерения. Случайные погрешности нельзя измерить и учесть, но можно оценить по законам математической статистики.

Величина систематической погрешности служит оценкой правильности измерения или метода измерения. Правиль­ность отражает близость полученного результата к истинно­му. Истинное значение обычно неизвестно. Сравнение часто проводят с действительным значением. Действительное зна­чение  — это экспериментально полученное или расчетное значение, настолько близкое к истинному, что может быть ис­пользовано вместо него. За действительное значение, например, может быть принято содержание определяемого компо­нента в стандартном образце.

Случайные погрешности характеризуют разброс результа­тов в серии измерений и определяют воспроизводимость из­мерений или метода.

Погрешности можно выразить абсолютной и относитель­ной величинами.

D = x_i - .

Здесь D — абсолютная погрешность (в тех же единицах, что и измеряемая величина); X_i — единичное измерение;  — истинное значение.

или

Здесь D — относительная погрешность (в процентах).

пример 1. В стандартном образце сплава с содержанием маг­ния 1.2•10^-2% атомно-абсорбпионным методом найдено 1.1•10^-2% магния. Рассчитайте абсолютную и относитель­ную погрешности.

Решение. D = 1.1•10^-2 - 1.2•10^-2 = -1.0•10^-3%

Оценка воспроизводимости

Результат единичного измерения не может служить надежной оценкой содержания определяемого компонента в образце или основой для серьезных выводов из экспериментальных дан­ных. Для получения надежного результата проводят серию параллельных измерений в идентичных условиях. Результат единичного измерения в такой серии называется вариантой, а вся серия — образует ряд вариант, выборочную совокупность или просто выборку.

Центр распределения выборки

В качестве центра распределения используют среднее (реже медиану М):

где x_i — единичный результат серии (варианта); n — число ва­риант.

Медиана М — это единичный результат, относительно ко­торого число полученных результатов с большим и меньшим значениями одинаково. При нечетном количестве результатов медиана совпадает с центральным числом выборки, при чет­ном она является средним арифметическим двух централь­ных результатов.

пример 2. Найдите среднее и медиану результатов определе­ния сульфат-иона в растворе серной кислоты (%): 24.05; 24.21; 24.33; 24.05; 24.22.

Решение. Находим среднее:

Для нахождения медианы располагаем результаты в по­рядке возрастания: 24.05; 24.05; 24.21; 24.22; 24.33. В дан­ном случае медианой является центральный результат

М = 24.21

пример 3. Найдите медиану результатов определения влаж­ности почвы (%): 5.31; 4.99; 5.26; 5.10.

Решение. Запишем выборку в порядке возрастания вариант:

4.99; 5.10; 5.26; 5.31. В данном случае имеется два цен­тральных значения, поскольку число результатов четное; поэтому

Критерии воспроизводимости

Критериями воспроизводимости служат а) отклонение от сред­него,

б) среднее отклонение от среднего,

в) отклонение и среднее отклонение от медианы,

г) размах варьирования,

д) дисперсия и

е) стандартное отклонение.

Отклонения могут быть выражены как абсолютными, так и относительными величинами.

Отклонение от среднего. Отклонение от среднего d — это раз­ность между единичным результатом и средним без учета знака. Среднее отклонение — это среднее арифметическое единичных отклонений:

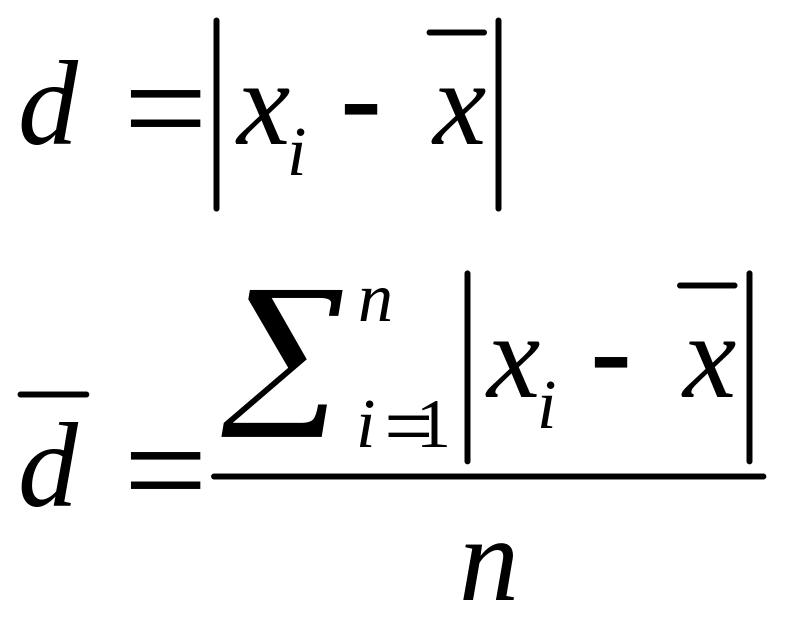
пример 4. Найдите отклонения от среднего и среднее откло­нение результатов определения объема колбы (мл): 50.05; 50.15; 49.90; 50.16; 50.00.

Решение. Находим среднее выборки:

Находим единичные отклонения:

d₁ = 50.05 - 50.05 = 0.00

d₂ = 50.15 - 50.05 = 0.10

d₃ = 49.90 - 50.05 = 0.15

d₄ = 50.16 - 50.05 = 0.11

d₅ = 50.00 - 50.05 = 0.05

Рассчитываем среднее отклонение:

Отклонение от медианы. Отклонение от медианы—это раз­ность между единичным результатом и медианой выборки без учета знака. Среднее отклонение от медианы—это среднее арифметическое отклонений от медианы.

пример 5. Найдите отклонение от медианы и среднее отклонение от медианы результатов, приведенных в примере 4.

Решение. Располагаем выборку в порядке возрастания ва­риант: 49.90; 50.00; 50.05; 50.15; 50.16. Видим, что М = 50.05 мл.

Находим единичные отклонения:

|49.90 - 50.05| = 0.15

|50.00 - 50.05| = 0.05

|50.05 - 50.05| = 0.00

|50.15 - 50.05| = 0.10

|50.16 - 50.05| = 0.11

Среднее отклонение от медианы равно

пример 6. Найдите относительное отклонение максимально­го и минимального результатов в выборке, приведенной в примере 4.

Решение. Находим отклонения:

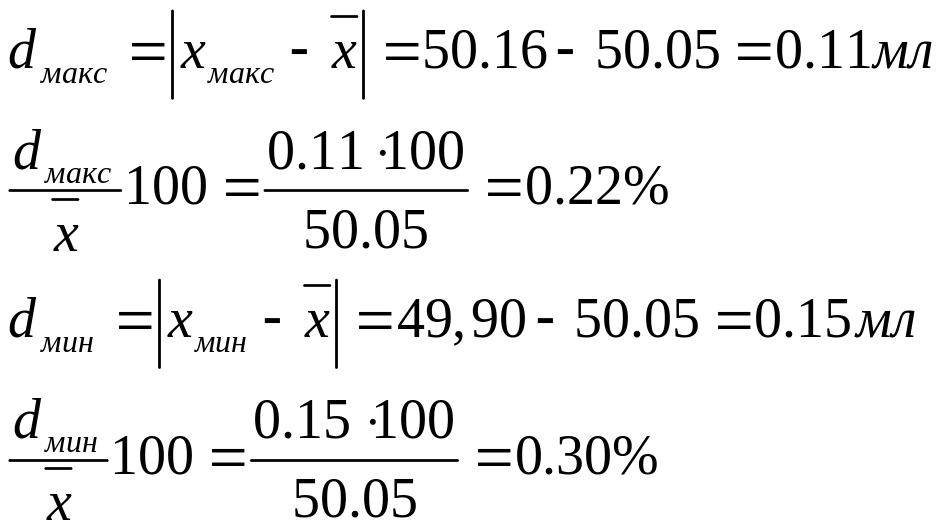
пример 7. Найдите относительное отклонение второго ре­зультата от медианы в выборке примера 4.

Решение, х₂ = 50.15 мл

Размах варьирования (диапазон выборки). Размах варьиро­вания  — это разность между максимальным и минималь­ным значениями выборки

 = x_макс ^— x_мин

пример 8. Каков размах варьирования выборки, приведен­ной в примере 4?

Решение. Максимальное значение в данной выборке 50.16, минимальное значение 49.90.

 = 50.16 - 49.90 = 0.26 мл

Дисперсия и стандартное отклонение. Более строгими крите­риями воспроизводимости, чем отклонение и размах варьиро­вания, являются дисперсия и стандартное отклонение.

Следует различать дисперсию и стандартное отклонение генеральной совокупности и выборочной совокупности (т.е. ряда из n вариант или выборки). Генеральная совокупность представляет собой гипотетическую совокупность, охватыва­ющую все мыслимые результаты от до . Выбороч­ная совокупность — это конечный ряд, включающий n вари­ант. При n>20 ряд можно считать с достаточной степенью приближения генеральной совокупностью. В генеральной со­вокупности среднее и истинное значения совпадают. В выбо­рочной совокупности среднее может отличаться от истинно­го значения. В генеральной совокупности все результаты и отклонения от среднего—независимые величины, т.е. число степеней свободы  равно числу вариант n. В выборке число степеней свободы равно числу вариант минус число связей, накладываемых на выборку.

И дисперсия, и стандартное отклонение характеризуют рассеяние вариант относительно среднего. Дисперсию V вы­борки вычисляют по формуле

Число степеней свободы меньше числа вариант на единицу, так как исключается степень свободы, связанная с определе­нием среднего. Если известно истинное значение, то

Стандартное отклонение выборки равно квадратному кор­ню из дисперсии, взятому с положительным знаком, и имеет размерность измеряемой величины:

Если известно истинное значение или выборка достаточ­но велика, используют стандартное отклонение генеральной совокупности :

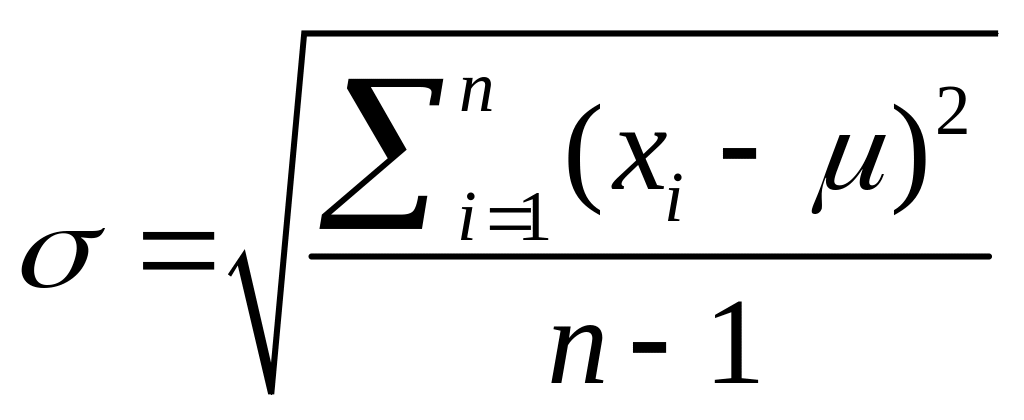
Стандартное отклонение генеральной совокупности и вы­борки связаны между собой:

Приближенно стандартное отклонение можно оценить по раз­маху варьирования:

или

где k — фактор отклонения, приводимый в справочниках для разного числа вариант n.

Используется также относительное стандартное отклоне­ние s_r:

пример 9. Рассчитайте дисперсию и стандартное отклонение (абсолютное и относительное) выборки из примера 4.

Решение. Воспользуемся величинами единичных отклонений, уже рассчитанными в примере 4:

а для вычисления s_r возьмем оттуда же значение среднего

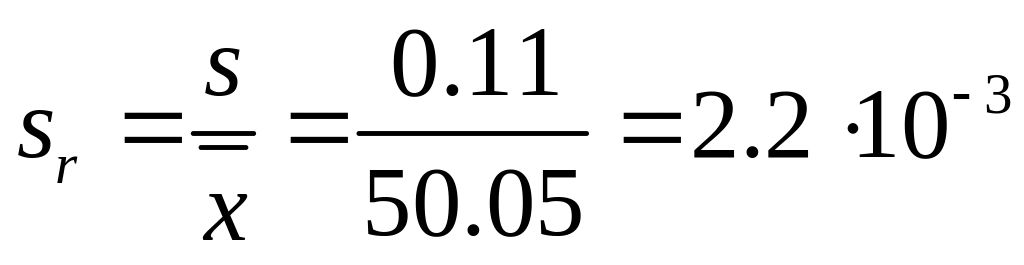
Пример 10. Рассчитайте стандартное отклонение по размаху варьирования выборки из примера 4.

Решение. Возьмем значение w из примера 8. Фактор откло­нения k находим в таблицах.