Министерство науки, высшей школы и технической политики РОССИЙСКОЙ ФЕДЕРАЦИИ

САМАРСКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕМКИЙ ИНСТИТУТ имени В. В. КУЙБЫШЕВА

Кафедра физики диффуузия и точечные дефекты в твердых телах. Механические свойства твердых тел

Методические указания для самостоятельной работы студентов по физике твердого тела

Самара 2015

Составитель: А. И. Волокитин УДК 539.1 Диффузия и точечные дефекты в твердых телах. Механические свойства твердых тел: Методические указания для самостоятельной работы студентов по физике твердого тела / Самара. Политехн. Ин-т; Сост. А. И. Волокитин. Самара, 1992. 16 с. Методические указания представляют собой задания для проведения самостоятельной работы студентов по физике твердого тела. Задания содержат теоретические вопросы, расчетные и проблемные задачи. Задания рассчитаны на студентов физико-технических специальностей вузов.

Печатается по решению редакционно-издательского совета СамПИ

Задание №1

Точечные дефекты в твердом теле

1. Дефекты Шоттки. Простейший тип дефектов возникает, когда атомы кристалла попадают из глубины кристалла на поверхность, образуя вакансии, которые называются дефектами Шоттки. Пусть на перемещение атома решетки на поверхность затрачивается энергия 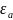и пусть при этом имеется n вакансий, хаотически распределенных по N узлам решетки. Число вакансий в термодинамическом равновесии находится из условия минимума термодинамического потенциала F=E-TS, где E=n - внутренняя энергия кристалла, содержащего nвакансий, T –температура, S –энторопия, которая определяется формулой Больцмана

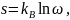
где 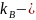постоянная Больцмана, 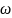- число способов, с помощью которых можно разместить n вакансий по N узлам решетки А. Доказать, что число способов разместить n вакансий по

узлам решетки равно

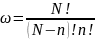
Б. Используя формулу Стирлинга, согласно которой 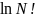≈ ≈NLnN при N>> 1, доказать, что

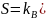В. Определить n из условия минимума термодинамического потенциала

Показать, что при N>>n

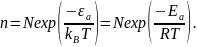
Г. Вычислить концентрацию вакансий с=n/N для меди, для которой при комнатной температуре (T = 300 K) и при предплавильной температуре (T = 1350 K).

2. Дефекты Френкеля. Иногда атомы, расположенные в узлах решетки, перемещаются в междоузельные промежутки, образуя дефекты Френкеля. Пусть – энергия, затрачиваемая на передвижение атома в междоузельный промежуток; N- число узлов решетки; N’- число внедренных промежутков узлов. С помощью метода, который использовался в предыдущем задании, показать, что число атомов n в междоузельных промежутках определяется формулой

exp

Для получения этой формулы необходимо сначала доказать, что число способов разместить N-n атомов по N узлам решетки и n атомов по N’ междоузельным промежуткам определяются формулой

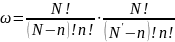
2. Энергия образования вакансий. Один из методов определения энергии образований вакансии состоит в следующем. Удельное электросопротивление металла 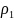измеряют при достаточно низкой температуре 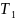(например комнатной). Затем образец нагревают до высокой температуры 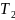» и после выдержки при этой температуре, достаточной для установления равновесной концентрации вакансии 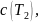быстро охлаждают (закаливают) до . Снова измеряют электросопротивление 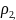при этом оказывается, что Увеличение электросопротивления связано с тем, что за время охлаждения вакансии не успевают уйти и их остается столько, сколько было при температуре . Предложить метод определения энергии образования вакансий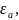 если известна зависимость 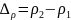от Считать, что электросопротивление пропорционально концентрации вакансий где - неизвестный коэффициент. Учесть, что если » , то 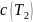» . 4. Концентрация вакансий. А. Пусть имеется линейная цепочка атомов. Расстояние между атомами, т. е. период цепочки обозначим через и длину цепочки через L. При достаточно низких температурах в цепочке нет пустых узлов, т. е. вакансий. При нагревании длина цепочки будет увеличиваться по двум причинам. Во-первых, при нагревании увеличивается расстояние между атомами. Относительное изменение периода решетки за счет теплового расширения составляет 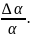Во-вторых, в металле при нагревании возникают вакансии, с каждой из которых связно увеличение длины цепочки на 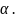Показать, что с случае линейной цепочки концентрация вакансий может быть определена из формулы , где относительное изменение длины цепочки, относительное изменение периода цепочки за счет теплового расширения.

Б. Пусть имеется длинный прямоугольный стержень с длинами сторон 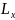, и . При нагревании линейные размеры стержня будут увеличиваться за счет теплового расширения и за счет образования вакансий и станут равными 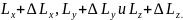Показать, что концентрация вакансий в стержне определяется формулой

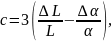
где 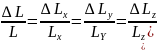- относительное изменение размеров тела, которое одинаково для всех трех взаимно перпендикулярных ребер стрежня , относительное изменение периода кристаллической решетки стрежня, которое так же одинаково для трех взаимно перпендикулярных кристаллических осей.

В. Дать описание эксперимента, с помощью которого может быть измерена равновесная концентрация вакансий в стрежне. Г. Определить относительное измерение длинны медного стержня при его нагревании от T= 300 К до Т=1350 К. Отдельно вычислить вклады за счет теплового расширения и за счет образования вакансий. Энергия образования вакансий в меди