Сетевое планирование.

1. Пусть есть конечное множество X = {x_i}, x_i  Х. Тогда можно получить граф G = {X, Г), где Г - закон соответствия множества Х графу G. Е сли X = {А, В, С, D, E) и ГА = {B, C, D}, ГB = {B}, ГC = {B, D, E}, ГD = {A, C} и ГЕ = О, то можно дать графическое и табличное представления графа

Основные понятия и определения:

Вершиной - графа называется элемент множества, образующего граф.

Дугой графа - ориентированная пара вершин графа.

Путем на графе - последовательность сцепленных дуг, позволяю­щих пройти из одной вершины

в другую.

Контуром - путь, начальная вершина которого совпадает с конечной.

Петля - дуга, начало и конец которой совпадают.

Ребром - неориентированная дуга, т. е. дуга, у которой не указано направление движения.

Цепь - сцепленная последовательность ребер или дуг.

Связный граф - между каждой парой его вершин существует хотя бы одна цепь.

Предок вершины - вершина, из которой выходит дуга, входящая в данную вершину.

Потомок вершины - вершина, в которую входит дуга, исходящая из данной вершины.

Граф G - множество вершин V, соединенных множеством ребер R, то есть G={V, R}.

Ориентированный граф (орграф) G - множество вершин V, соединенных множеством дуг D, то есть G={V, D}.

II. Для связного графа без контуров решается задача декомпозиции его вершин на слои так, чтобы:

1). все элементы (вершины) данного слоя не имели предков в предыдущем слое, а элементы последнего слоя - потомков;

2). порядок вершин внутри одного и того же слоя безразличен.

Решение этой задачи осуществляется путем последовательного вычеркивания (фиксации) вершин, не имеющих предков, которые и составляют соответствующий слой.

П усть имеется орграф без контуров вида (Рис.1):

1. Вершина А не имеет предков - она образует 1-й слой. Вершину вычеркивают вместе с дугами, которые из неё выходят, и получают новый орграф вида Рис.2.

3. Вершина G не имеет предков, то есть образует 3-й слой. Вершину G вычеркивают вместе с исходящими из неё дугами и получают новый орграф вида Рис.4

2. На полученном орграфе вершины C, D, B не имеют предков, то есть они образуют 2-й слой.

Вершины C, D, B вычеркивают вместе с дугами, изходящими из них и получают новый орграф вида Рис.3

4. Вершины E, F не имеет предков, то есть образуют 4-й слой. Вершины E, F вычеркивают вместе с исходящими из них дугами и получают новый орграф вида Рис.5

3. Вершина G не имеет предков, то есть образует 3-й слой. Вершину G вычеркивают вместе с исходящими из неё дугами и получают новый орграф вида Рис.4

5. Вершины H, L не имеют предков, то есть образуют 5-й слой. Вершины H, L вычеркивают вместе с исходящими из них дугами и получатют новый орграф в виде Рис. 6

6. Вершина К не имеет предков, то есть образует 6-й слой. Вершину К вычеркивают вместе с исходящей из неё дугой и остается вершина, не имеющая предков, то есть образующая 7-й слой. Рис. 7 - последний, так как у вершины М нет потоков.

В результате проведенной декомпозиции исходный орграф (Рис.1) можно представить в упорядоченном виде, то есть в виде слоев (Рис.8), что упрощает анализ структуры графа.

С E H

А D G F L K M

B

Слои 1 2 3 4 5 6 7

Рис.8

III. Проект - совокупность действий, выполнение которых необходимо для достижения некоторой цели (наступления события), причем длительность реализации (выполнения) каждого действия известна и они связаны отношением порядка (обязательным предшествованием).

Ход выполнения проекта иллюстрируют сетевым графиком, представляющим собой взвешенный орграф, в котором вершины - это события от Е₁ до Е_n, которые должны возникать по мере осуществления проекта, а дуги - это переходы от одного события Е_i к другому E_j, то есть процессы выполнения действий P_ij .Дугам приписывают продолжительности ваыполнения соответствующих действий (часы, дни, недели, месяцы и т.п.) - этим определяется взвешенность орграфа (сетевого графика осуществления проекта).

4 Е₄

10 Р_4,8 5 6

Р_6,8 Е₆

8

Е₈

На Рис.9 представлен фрагмент сетевого графика, который соответствует части проекта строительства объекта.

Событие Е₁ - "начало выполнения проекта".

Событие Е_n - "окончание выполнения проекта".

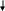
Рис.9

Например, событие Е₈ - "начало закладки фундамента", а действия, предшествующие этому событию: (Р_4,8) - "рытье котлована под фундамент" и (Р_6,8) - "подвозка железнодетонных блоков для фундамента". Продолжительность Р_4,8 10 временных единиц, а Р_6,8 – пять.

.

Из сетевого графика проекта (Рис.10) видно:

1) от события Е₁ к событию Е_n можно пройти различными путями;

2) наступление каждого последующего события может произойти только тогда, когда будет завершено самое продолжительное действие, обуславливающее его наступление;

3) самый длинный путь в сетевом графике определяет кратчайшие сроки осуществления проекта - это критический путь;

4) события и действия, не лежащие на критическом пути (лежат на более коротких путях сетевого графика) могут выполняться с резервом времени, без угрозы срыва общего срока осуществления проекта.

IV. Пусть в результате декомпозиции полного сетевого графика на слои выделен некоторый k-й слои, взвешенный орграф которого представлен на Рис.10.

0

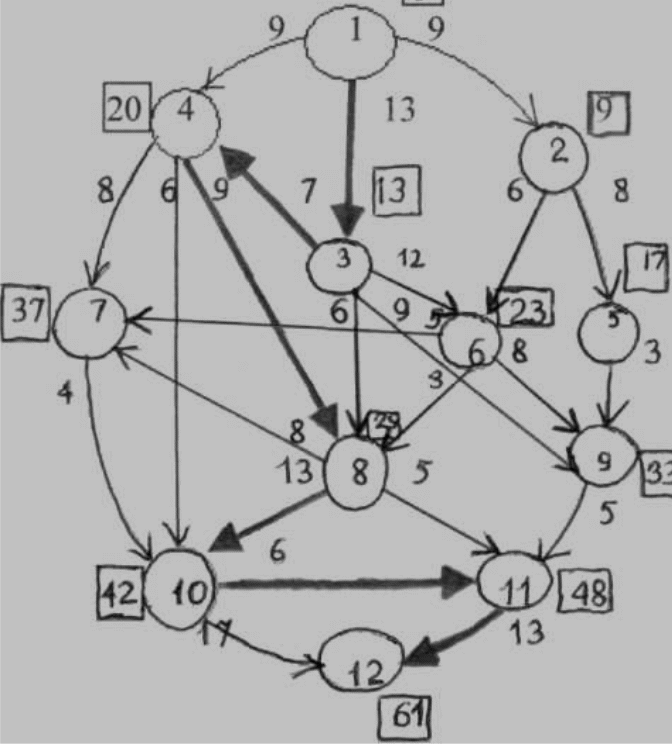
Рис. 10

Алгоритм определения времени насатупления событий Е₂…Е_12:

1. Событию Е₁ приписывается t₁ = 0.

2. Для каждой вершины Е₂…Е₁₂ рассматриваются дуги, которые из неё выходят.

3. Для каждой из выделенных дуг суммируется время соответствующего действия, которое приписано дуге (вес дуги в единицах времени), с временем наступления события, соответствующего началу дуги.

4. Сравниваются результаты, выбирается из них наибольший и приписывается вершине (событию), соответствующей концу дуги.

Пример:

1.Из Е₁ выходят три дуги: Р_1,2 с весом 8, Р_1,3 с весом 13 и Р_1,4 с весом 9. Так как для Е₁ принято t₁ = 0, то 0+8=8, 0+13=13, 0+9=9 и, следовательно, событию Е₃ приписывается t₃ = 13, а дуга Р_1,3 входит в критический путь.

1. Из Е₃ входят четыре дуги: Р_3,4, Р_3,8, Р_3,9 и Р_3,6 , но Е₃ непосредственно связано с Е₄, следовательно, в критический путь входит дуга Р_3,4 с весом 7, а время наступления события Е₄ равно t₄ = 13+7=20, кроме того Р_1,3+Р_3,4 = 20, Р_3,8 = 6, Р_3,9 = 9 и Р_3,6 = 12, то есть выбирается Р_1,3 + Р_3,4 =20.

2. Из Е₄ выходят три дуги Р_4,7 с весом 8, Р_4,10 с весом 6 и Р_4,8 с весом 9. Так как t₄ = 20, то 20+8=28, 20+6=26, 20+9=29 и, следовательно, событию Е₈ приписывается t₈=29, а дуга Р_4,8 входит в критический путь.

3. Из Е₈ выходят три дуги Р_8,7 с весом 8, Р_8,10 с весом 13 и Р_8,11 с весом. Так как t₈=29, то 29+8=37, 29+13=42, 29+5=34 и, следовательно, событию Е₁₀ приписывается t₁₀=42, а дуга Р_8,10 входит в критический путь.

4. Из Е₁₀ выходят две дуги Р_10,11 с весом 6 и Р_10,12 с весом 17, но Е₁₀ непосредственно связано с Е₁₁, следовательно, в критический путь входит дуга Р_10,11 с весом 6, а время наступления события Е₁₁ равно t₁₁=42+6=48, кроме того Р_10,11+Р_11,12=19, а Р_10,12=17, то есть выбирается Р_10,11+Р_11,12=19.

5. Из Е₁₁выходит только одна дуга Р_11,12 с весом 13, она и входит в критический путь.

Следовательно, проект может быть реализован, то есть наступят все 12 событий, за 61 единицу времени. Действия, соответствующие дугам Р_1,3, Р_3,4, Р_4,8, Р_8,10, Р_10,11, Р_11,12, составляют критический путь : Е₁, Е₃, Е₄, Е₈, Е₁₀, Е₁₁, Е₁₂.

V. Следует обозначить t_i - ранний срок (ожидаемое время) наступления события Е_i. a t^*_i - предельный срок (предельное время) наступления события Е_i , превышение которого приведет к увеличению времени реализации всего проекта. При этом, следует учесть, что для критических событийц (Е₁, Е₃, Е₄, Е₈, Е₁₀, Е₁₁, Е₁₂ на Рис.10) должно выполняться условие t^*_i = t_i, так как такое событие не допускает никакого запаздывания в сроках его наступления, то есть критические действия (Р_1,3, Р_3,4, Р_4,8, Р_8,10, Р_10,11, Р_11,12 на Рис.10) не допускают никакой зедержки в их выполнении.

Резервным интервалом события Е_i (интервалом свободы события) [t_i. t^*_i] называют интервал времени, в течении которого может наступить событие Е_i без изменения общего времени реализации проекта t_n . Определение резервных интервалов событий осуществляется по сетевому графику (Рис.10), идя от конечного события Е₁₂, то есть снизу вверх.

Пример:

1. Наступление события Е₇ отделено от наступления события Е₁₀ действием длительностью 4 единицы времени, то есть действие Р_7,10 может начатся за 4 единицы времени до наступления события Е₁₀. Следовательно, событие Е₇ должно произойти в интервале [37, 42-4=38].

2. Наступление события Е₉ отдельно от наступления события Е₁₁ на 5 единиц времени и поэтому событие Е₉ должно прроизойти в интервале [33, 48-5=43].

3. Событие Е₆ отделяет от события Е₉ действие Р_6,9, выполняемое за 8 единиц времени, от события Е₈ - 3 единицы времени, от события Е₇ - 5 единиц времени. Производится сравнение 33-8=25, 29-3=26, 37-5=32. Наименьшая из сравниваемых величин и есть верхняя граница интервала [23, 25].

4. Событие Е₅ отделяется от события Е₉ три единицы времени, то есть резервный интервал для события Е₅ равен [17, 33-3=30].

5. Событие Е₂ отделяет от Е₅ и Е₆ соответственно 9 и 6 единиц времени, тогда 17-8=9, 23-6=17 и, выбирая наименьшее значение, получают резервный интервал для Е₂ равный [8, 9].

Следовательно, моменты наступления событий Е₂, Е₅, Е₆, Е₇, Е₉ могут быть в следующих интервалах:

Е₁: 0,Е₂: [8, 9], Е₃: 13, Е₄:20, Е₅: [17, 30], Е₆: [23, 25],

Е₇: [37, 38], Е₈:29, Е₉: [33, 43], Е₁₀:42, Е₁₁48, Е₁₂:61,

а на критическом пути интервалы сводятся к точечным моментам времени.

VI. Для каждого действия Р_ij необходимо определить какая задержка модет быть допущена при его выполнении без того чтобы это привело к нарушению срока наступления события Е_j. Для каждого действия существует три резерва времени:

1) свободный резерв времени - это возможная отсрочка начала выполнения действия, обозначается R1_ij, то есть если t_i и t_j - ожидаемые сроки наступления событий Еi и Еj, между которыми происходит действие Р_ij длительнотью t_ij , то

R1_ij = t_j - t_i - t_ij;

свободный резерв времени критических действий равен нулю, так как они не могут быть задержаны;

2) полный резерв времени действия Р_ij определяется по формуле

R2_ij =t^*_j - t_i - t_ij;

3) независимый резерв времени действия Р_ij определяется по формуле

R3_ij = t_j - t^*_i - t_ij;

или, чтобы не получать отрицательныхз значений R3_ij = max (0, t_j - t^*_i - t_ij).

Резервы наступления событий и выполнения действий характеризуют эластичность проекта: чем меньше резервы, тем ближе проект к критичекому пути.

Существенное различие между резервным интервалом события Еi и свободным или полным резервом действия Р_ij состоит в том, что:

• резервный интервал события - это запаздывание, которое может быть допущено в наступлении события Еi без изменения фиксированных сроков наступления критических событий и, в частности, конечного, то есть без изменения t_n,

• свободный резерв действия - это отсрочка начала выполнения действия Р_ij без изменения ожидаемого срока наступления события Еj, а полный резерв действия - это максимально допустимая отсрочка начала выполнения действия Р_ij .

Пример:

1. В предыдущем примере определено, что интервал свободы события Е₆ есть [23, 25]. Тогда свободный резерв действия Р_6,9 равен

R1_6.9 = t₉ - t₆ - t_6.9 = 33 - 23 - 8 = 2 единицы времени.

Следовательно, действие Р_6,9 может начаться в момент 23+2=25 без изменения времени (срока) наступления события Е₉, который равен t₉ = 33 единицы времени.

Аналогично определяются свободные резервы времени для всех остальных действий.

2. Полный резерв действия Р_6,9 равен

R2_6.9 = t^*₉ - t₆ - t_6,9 = 43 - 23 - 8 = 12

Следовательно, действие Р_6,9 может начаться в момент 23+12=35, не вызывая задержку в реализации проекта.

3. Независимый резерв действия Р_6,9 равен

R3_6.9 = t₉ - t ^*₆ - t_6,9 = 33 - 25 - 8 = 0.

Пример 6.