Транспортная задача.

I. Одной из часто встречающихся задач хозяйственного управления является задача по разработке рационального плана транспортных перевозок, то есть минимизация затрат на их выполнение. Формулировка транспортной задачи в общем виде: требуется перевезти определенное количество однородного груза из m пунктов отправления в п пунктов назначения. Вводят обозначения:

а_i — общее количество груза в i-м пункте отправления;

b_j — общее количество груза, необходимое в j-м пункте назначения;

c_ij - затраты на транспортировку единицы груза из i-го пункта отправления в j-й пункт назначения;

Z - совокупные затраты на транспортировку всего груза;

x_ij - исходное неизвестное количество груза, которое перевозится из пункта i в пункт j.

Из условия задачи следует модель линейного программирования:

• целевая функция 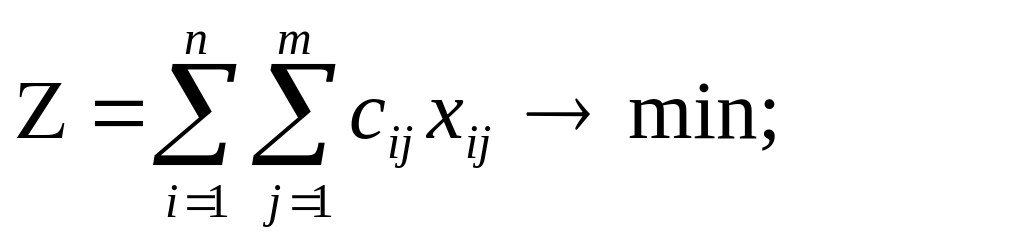(1)

• 1-я система ограничений 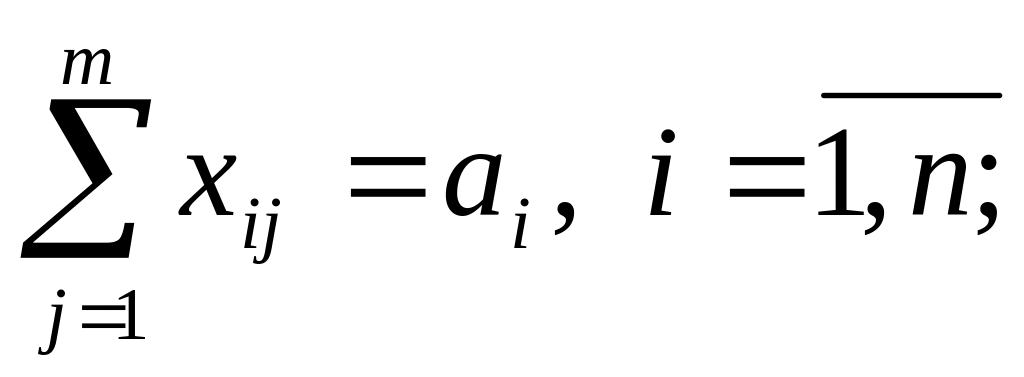(2)

• 2-я система ограничений 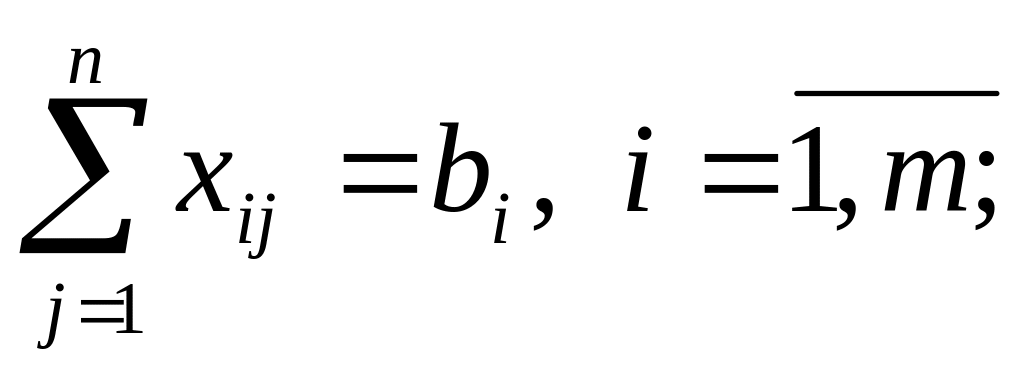(3)

• 3-я система ограничений 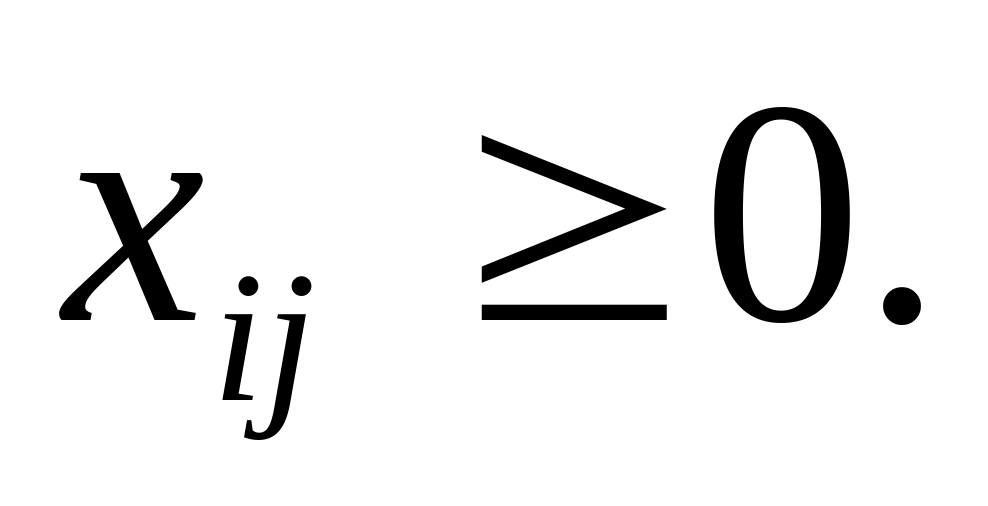(4)

Система ограничений (2) говорит о том, что весь груз из каждого пункта его сисредоточения должен быть вывезен, система ограничений (3) - потребность в грузе в каждом пункте должна быть удовлетворена, система ограничений (4) - по любому маршруту либо перевозится некоторое количество груза x_ij > 0, либо нет x_ij = 0.

Следовательно, транспортная задача является задачей линейного программирования

с n + m ограничениями, то есть с уравнениями с n + m неизвестными. Транспортная задача, у которой суммарное наличие груза совпадает с суммарной потребностью, то есть выполняется условие

(5)

называется сбалансированной (закрытой), а если условие (5) не выполняется, то открытой (решение открытой сводится к решению закрытой).

Выполнение условия (5) позволяет исключить одно из ограничений (2) или (3) и свести их число к n + m - 1. Иными словами, если выполняетс условие (5), то любая транспортная задача имеет оптимально допустимое решение (план), содержащее не более n + m - 1 компонент.

II. Пример.

Для решения транспортной задачи используют распределительный метод, реализуемый на основе алгоритма:

1. Формирование таблицы исходных данных в виде

Таблица 1

	В1	В2	В3	В4	В5	Наличие
А1	2	4	5	7	9	300
А2	1	6	3	5	4	400
А3	6	3	2	1	10	900
Потребность	250	300	350	500	200	1600

А1, А2, А3 - пункты отправления груза, n = 3.

B1, B2, B3, B4, B5 - пункты назначения груза, m = 5.

В столбе "Наличие" - какое количесвто груза в каждом пункте отправления А1, А2, А3.

В строке "Потребность" - потребности в этом грузе каждого пункта назначения.

Модель задачи "Закрытая", так как суммы потребностей и возможностей (наличия) равны 1600.

В верхних левых углах каждой клетки таблицы, которые соответствуют всем возможным путям перемещения груза из всех пунктов отправления во все пункты назначения, указаны затраты С на транспортировку единицы груза по данному маршруту.

2. Аналитическая форма модели имеет вид

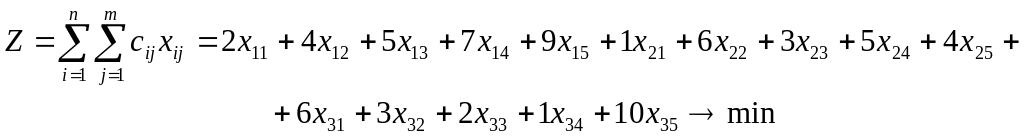(6)

х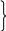 ₁₁ + х₁₂ + х₁₃ + х₁₄ + х₁₅ = 300

х₂₁ + х₂₂ + х₂₃ + х₂₄ + х₂₅ = 400 (7)

х₃₁ + х₃₂ + х₃₃ + х₃₄ + х₃₅ = 900

х ₁₁ + х₂₁ + х₃₁ = 250

х₁₂ + х₂₂ + х₃₂ = 300

х₁₃ + х₂₃ + х₃₃ = 350 (8)

х₁₄ + х₂₄ + х₃₄ = 500

х₁₅ + х₂₅ + х₃₅ = 200

3. Выполнение правила "Северо-Западного угла": Распределение груза начинается с левого верхнего угла и заканчивается правым нижним углом исходной (транспортной) таблицы.

   1. При этом для получения исходного базисного решения должны выполняться условия:

• количество компонент не должно превосходить числа n + m - 1,

• должны соблюдаться ограничения (2) и (3).

1. Осуществление распределения груза между пунктами отправления и назначения:

• из А1 и В1 отправляется 250 единиц груза, то есть потребность В1 полностью удовлетворена,

• остаток груза в А1 (50 единиц) направляется в В2 и для полного удовлетворения его потребности из А2 отправляется 250 единиц груза из имеемых 400 (остаток в А2 150 единиц),

• аналогичным образом, сохраняя баланс по столбцам и строкам, заполняются остальные клетки исходной таблицы, которые определяют исходные маршруты перевозки груза и формируется табл.2.

1 2 3 4 5 Таблица 2.

		В1	В2	В3	В4	В5	Наличие
1	А1	2 250	4 50	5	7	9	300
2	А2	1	6 250	3 150	5	4	400
3	А3	6	3	2 200	1 500	10 200	900
	Потребность	250	300	350	500	200	1600

3. Получение плана перевозок путем подсчета затрат на его реализацию:

- перемножение транспортных тарифов (верхний левый угол таблицы на объем перевозок

500 200 450

1500 400

500. 2000

• найти сумму

Z = 500 + 200 + 1500 + 450 + 400 + 500 + 2000 = 5550

4. Выполнение правила "наименьшего элемента в строке" (или "наименьшего элемента в столбце"): первоначально по строкам (по столбцам) заполняются те клетки исходной таблицы, то есть выбираются те маршруты перевозки грузов, для которых затраты на перевозку минимальны в строке (в столбце).

4.1 Заполнение клеток таблицы, в которых минимальны затраты первозок единицы груза (если одинаковы, то предпочтение выбору маршрута произвольно). В этом случае опорный план, составленный по правилу "наименьшего элемента", имеет вид

Таблица 3.

	В1	В2	В3	В4	В5	Наличие
А1	2	4 250	5	7	9 50	300
А2	1 250	6	3	5	4 150	400
А3	6	3 50	2 350	1 500	10	900
Потребность	250	300	350	500	200	1600

2. Определение суммы

Z = 250 + 1000 + 150 + 700 + 500 + 450 + 600 = 3650 - это базисное решение (базисный план)

4. Проверка базисного решения на оптимальность, для чего вводятся два понятия:

1) цикл (замкнутый) свободной клетки - это последовательность клеток (i, j), котоая начинается со свободной (пустой) клетки и ею же заканчивается, причем в каждой строке и в каждом столбце при построении цикла должны быть использованы две и только две клетки (при этом: никакая последовательность занятых клеток не образует цикл и каждой свободной клетке соответствует единственный цикл);

2). оценка овободной клетки - разность между суммами тарифов c_ij в клетках цикла со знаком "+" и со знаком "-" (клетки цикла, начиная с пустой, обозначаются чередующимися знаками +, -, +, - и так далее)

где индексы (i, j) соответствуют номеру пустой клетки, а индексы (k, e) - заполненными клеткам в цикле; оценка свободной клетки показывает, на сколько измениться величина суммарных затрат на перевозку всего груза, если перебросить единицу груза на маршрут, соответствующий пустой клетке, при этом не нарушив баланса по потребности (спросу) и наличием (пердложению).

2. Построение циклов пустых клеток для табл. 2, осуществляя движение против движения часовой стрелки (можно по движению)

• в табл. 2 восемь сводобных клеток с индексами (1,3), (1,4), (1,5), (2,1), (2,4) (2,5), (3,1), (3,2),

• циклы пустых клеток:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

• последовательная нумеровка входящих клеток каждого цикла порядковыми номерами. начиная с пустой клетки, или обозначения их знаками +, -, +, - и т.д.

2. Определение сумм тарифов стоящих в клетках циклов со знаком "+" и знаком "-":

• со знаком "+" (5+6); (7+6+3); (9+6+2+10); (1+4); (5+2); (4+2+10); (6+3+1); (3+6)

• со знаком "-" (4+3); (4+3+1); (4+3+1); (6+2); (3+1); (3+1); (2+6+2); (2+6)

2. Определение разностей

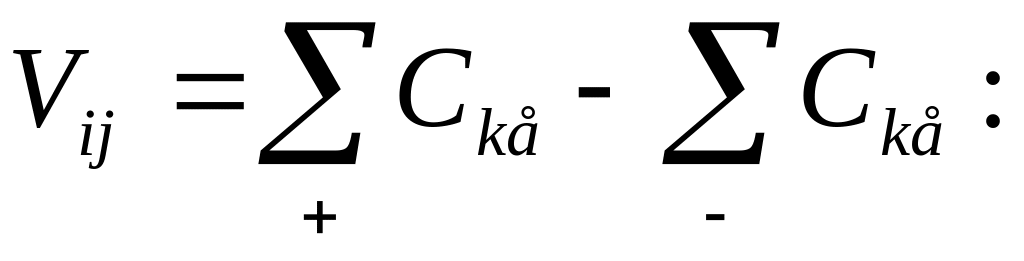
V_1,3 = (5+6) - (4+3) = 4

V_1,4 = (7+6+3) - (4+3+1) = 16 - 8 = 8

V_1,5 = (9+6+2+10) - (4+3+1) = 19

V_2,1 = (1+4) - (6+2) = -3

V_2,4 = (5+2) - (3+1) = 7 - 4 = 3

V_2,5 = (4+2+10) - (3+1) = 16 - 4 = 12

V_3,1 = (6+3+1) - (2+6+2) = 10 - 10 = 0

V_3,2 = (3+6) - (2+6) = 9 - 8 = 1

Так как среди V_ij есть отрицательная V_2,1 = -3, то исходный план перевозок может быть улучшен.

6. Улучшение исходного плана:

• в цикле свободной клетки с минимальной отрицательной оценкой V_ij (если таких оценок больше одной) выбирается минимальное значение груза в клетках со знаком "-" и помещается в свободную клетку;

- так как в 1,1 и 2,2 одинаковое количество груза по 250 единиц, то в свободную клетку 2,1 помещается 250 единиц груза;

• перераспределение груза по циклу: найденное минимальное количество груза добавляются к грузу в клетках со знаком "+" и вычитается из груза в клетках со знаком "-",

то есть в клетке 1,2 будет 300 единиц груза, а клетки 1,1 и 2,2 окажутся пустыми;

• выполнение п.5 - проверка оптимальности нового плана

	В1	В2	В3	В4	В5	Наличие
А1	2	4 300	5	7	9	300
А2	1 250	6	3 150	5	4	400
А3	6	3	2 200	1 500	10 200	900
Потребность	250	300	350	500	200	1600

путем подсчета оценок свободных клеток V_ij ;

• вычислительный процесс продолжается до тех пор пока все оценки свободных клеток станут положительными или равными нулю.

Пример 5.