Примеры решения задач

Теория вероятностей – это раздел математики, изучающий количественные закономерности случайных явлений, т.е. таких, которые при неоднократном воспроизведении в одинаковых условиях могут протекать по разному. Объектами, которыми оперирует теория вероятностей, являются:

• Случайное событие – всякий факт, который может произойти или не произойти в результате случайного явления;

• случайная величина – некоторое числовое значение появляющееся в результате случайного явления.

Задача 7. Дано вероятность попадания по мишени – 0,3. Требуется определить вероятность попадания с третьего раза.

Решение: Последнее событие наступает при одновременном наступлении: 1) первый раз промахнулся; 2) второй раз промахнулся; 3) третий раз попал.

p(Ā Ā A) = p(Ā)p(Ā)p(A)=0,70,70,3 = 0,147

Задача 8. Дано среди 10 шаров 2 – черные. Требуется определить вероятность с двух попыток вытащить оба этих шара?

Решение. Обозначив A – первый раз вытащить черный, B - второй раз вытащить черный: p(оба раза - черные) = p(AB) = p(A)  p(B|A) = 2/10  1/9 = 1/45

Задача 9. Дано среди 10 шаров 1 – черный. Десять человек по очереди вытаскивают шар. Требуется определить у кого из них наибольшая вероятность вытащить черный?

Решение. Обозначив A₁ – первый вытащил черный шар,... p(A₁) = 1/10; p(второму достался черный) = p(Ā₁A₂) = p(Ā₁)  p(A₂ /Ā₁) = 9/10  1/9 = 1/10; p(третьему достался черный) = p(Ā₁Ā₂A₃) = p(Ā₁)  p(Ā₂ / Ā₁)  p(A₃ /Ā₂ Ā₁) = 9/10  8/9 1/8 = 1/10 и т.д.,

т.е. все участники розыгрыша имеют одинаковые шансы вытащить черный шар независимо от порядка вытаскивания.

Задача 10. Дано участники группы захвата и группы поддержки атакуют преступников и производят по месту их укрытия две независимые очереди из автоматического оружия. Вероятность поразить цель первой очередью равна 0,2, второй - 0,3. Если преступники не поражены, то они оказывают вооруженное сопротивление и поражают участников операции с вероятностью 0,25. Требуется определить вероятность потерь среди участников операции при условии, что преступники не поражены.

Решение: 1. При использовании теоремы сложения и умножения вероятностей можно определить вероятность поражения от применения оружия с обеих сторон - сотрудников органов внутренних дел и преступников.

2. Вероятность не поражения преступников первой очередью:

Р1 = 1 - 0,2 = 0,8;

3. Вероятность не поражения преступников второй очередью:

Р2 = 1 - 0,3 = 0,7;

4. Вероятность не поражения преступников:

Р = Р1*Р2 = 0,8*0,7 = 0,56;

5. Вероятность поражения преступников

1 - Р = 1 - 0,56 = 0,44.

6. Вероятность потерь среди участников операции:

Р*0,25 = 0,56*0,25 = 0,14.

Задача 11. Дано всхожесть семян данного растения составляет 90 %. Требуется найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.

Решение. 1. Если производится п независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события равна q=1-p, то вероятность Р_п(т) того, что при этом событие А осуществляется ровно т раз, вычисляется по формуле Бернулли

(1)

где есть число сочетаний из п элементов по т.

2. По условию задачи вероятность всхожести семян р=0,9; тогда q=0,1; в данном случае п=5 и т=4. Подставляя эти данные в формулу Бернулли (1), получают

3. Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом, Р(А)=Р₅(4)+Р₅(5). Первое слагаемое уже найдено. Для вычисления второго снова применяют формулу (1):

Следовательно, Р(А)=0,328+0,591=0,919.

Задача 12. Дано вероятность появления события А в каждом из 625 испытаний равна 0,64. Требуется найти вероятность того, что событие А в этих испытаниях появиться ровно 415 раз.

Решение. 1. Если число испытаний п велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях применяют приближенную формулу, которая выражает суть локальной теоремы Лапласа.

Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р, а число п достаточно велико, то вероятность Р_п(т) того, что в этих испытаниях событие А наступит т раз (безразлично, в какой последовательности) вычисляется приближенно по формуле

(2)

где

Имеются готовые таблицы значений функции (х) (табл. П.1).

2. Для х5 считают, что (х)0. Так как функция (х) четная, то (-х)=(х). По условию задачи п=625, т=415, р=0,64. Находят q=1-0,64=036. Определяют значение х при этих данных:

3. По табл. П1 находят, что (1,25)=0,1826. Подставив это значение в (2), получают

Задача 13. Дано среди семян ржи 0,04 % сорняков. Требуется определить вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

Решение. 1. Применение асимптотической формулы (2) для случая, когда вероятность р близка к нулю, приводит к значительному отклонению от точного значения Р_п(т). При малых значениях р (и при малых значениях q) применяют асимптотическую формулу Пуассона.

Если вероятность появления события А в каждом из п независимых испытаний мала, а число испытаний п достаточно велико, то вероятность того, что событие А наступит т раз, вычисляется приближенно по формуле

(3)

где =пр.

Формулу (3) применяют в тех случаях, когда 10. При этом чем больше число п и меньше число р, тем точнее результат по этой формуле.

2. По условию задачи п=5000, т=5, р=0,0004. Тогда =5000^.0,0004=2. Применяя (3), получают

Задача 14. Дано : имеются три одинаковых на вид урны. В них находятся:

в первой урне – 2 белых и 1 черный шар;

во второй урне – 3 белых и 1 черный шар;

в третьей урне – 2 белых и 2 черных шара.

Требуется :

• некто выбирает наугад одну из урн и вынимает из нее шар, найти вероятность того, что это шар белый.

• из случайно выбранной урны вытащен белый шар, найти вероятность того, что он вытащен из второй урны.

Решение. 1. Рассматривают три гипотезы:

- выбор первой урны,

- выбор второй урны,

- выбор третьей урны,

и событие А - появление белого шара.

2. По условию гипотезы равновозможны, следовательно, их вероятности равны

Р( )=Р( )=Р( )= .

3. Найдем условные вероятности события А при этих гипотезах:

; ; .

4. Так как гипотезы , и - несовместны и образуют полную группу, то для расчета требуемой вероятности события А применима формула полной вероятности:

.

5. Вероятность того, что белый шар вытащен из второй урны, рассчитаем по формуле Байеса:

.
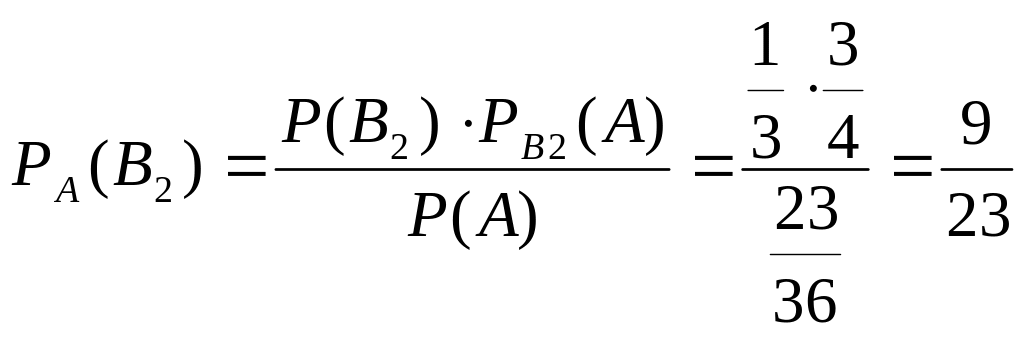