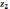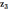3. Построение картины зацепления

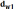Для построения картины зацепления проводим межосевую линию и наносим на ней отрезок , изображающий межосевое расстояние передачи . Из центра колес проводим начальные окружности, касающиеся друг друга в точке П₁₂, называемой полюсом зацепления. Диаметры начальных окружностей и берутся из распечатки.

Расположим зуб первого колеса симметрично относительно межосевой линии. Определим положение осей симметрии двух соседних зубьев первого колеса, для чего из точки П₁₂ радиусом равным шагу по хорде начальной окружности 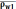, сделаем засечки на начальной окружности первого колеса и полученные точки 1 и 2 соединим с центром колеса О₁.

Для построения эвольвентных участков профилей зубьев проводим основную окружность и окружность вершин, а также две вспомогательные окружности, проходящие через точки к = 0,5 и к = -0,5. Точка к = 0,5 делит пополам расстояние между окружностью вершин и начальной окружностью, а точка к = -0,5 – расстояние между начальной и основной окружностями.

После этого на каждой из пяти окружностей из точек, лежащих на пересечении их с осями симметрии зубьев, радиусами равными хордам половины толщины зуба на соответствующей окружности делаем засечки. Полученные точки пересечения принадлежат эвольвентам, по которым расчерчиваются правый и левый профили зуба.

Переходные участки профилей зубьев условно вычерчиваются по дуге окружности радиуса .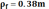

Для построения их проведем окружность впадин первого колеса; отложим от нее на оси симметрии зуба величину 0,38m и через полученную точку проведем вспомогательную окружность. Из точек пересечения ее с эвольвентами профилей зуба радиусом находим положение точек, которые являются центрами дуu окружностей сопрягающих эвольвентные участки профилей зуба с окружностью впадин.

Для построения профилей зубьев второго колеса найдем положение осей симметрии. Из полюса П₁₂ , через который проходит ось симметрии впадины между зубьями второго колеса радиусом равным шагу по хорде начальной окружности второго колеса 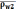, делаем засечки на начальной окружности второго колеса справа и слева от П₁₂, полученные при этом точки 3 и 4 определяют положение осей симметрии впадин. Оси симметрии зубьев второго колеса проходят через середины отрезков .

Построение профилей зубьев второго колеса выполняется аналогично для колеса 1.

Коэффициент перекрытия равен

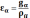
где 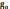– длина зацепления

– шаг зацепления

Их значения берутся из полученного чертежа.

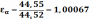
3. Исследование планетарных механизмов

   1. Исходные данные

Число оборотов на входе редуктора

Число оборотов на выходе редуктора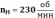

m=6 мм

Механизм состоит из двух ступеней. Первая - рядовая ступень с внутренним зацеплением. Вторая – планетарная ступень со сдвоенными сателлитами.

2. Разбивка общего передаточного отношения по ступеням

Первая ступень рядовая, передаточное число равно u₁₂, вторая ступень планетарная, передаточное число равно u_3H

Для цилиндрической зубчатой передачи передаточное число принимают от 3 до 7. В данной планетарной ступени передаточное число принимают от 5 до 30.

Принимаем 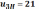, тогда

3. Подбор чисел зубьев планетарного механизма

Число зубьев для цилиндрической зубчатой передачи с внутренним зацеплением равно

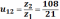
Для определения числа зубьев планетарной ступени необходимо прибегнуть к следующим формулам

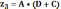
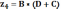
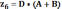
Причем необходимо соблюдать соосность

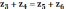
Для определения коэффициентов A, B, C, D необходима следующая формула

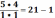
A=1 B=4 C=1 D=5

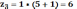
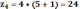
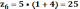
Умножаем все на одинаковый целый множитель 4

Полученные количества зубьев приведено в таблице 4

Таблица 4

Количествo зубьев

21	108	24	96	20	100