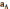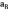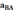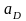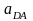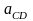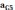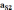- •Расчетно-пояснительная записка к курсовой работе по дисциплине «Теория механизмов и машин»
- •Оглавление
- •Определение ускорений
- •Силовой анализ механизма
- •Определение давлений в шарнирах
- •Определение момента, приложенного к кривошипу
- •Определение момента методом рычага Жуковского
- •Исследование эвольвентного зацепления
- •Исходные данные
- •Выбор коэффициентов смещения режущего инструмента при помощи блокирующих контуров
- •Построение картины зацепления
- •Определение числа сателлитов
- •Проверка возможности сборки
- •Кинематический расчет редуктора графоаналитическим методом
Определение ускорений
Перейдем теперь к определению ускорений. Ускорение точки А определяется по формуле
 ,
м/с2,
,
м/с2,
(так как ω1=const и ε1=0) и направлено от точки А к точке О.
Ускорение точки B находится из уравнения
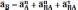
где
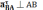
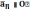
В
этом уравнении 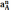 получено
выше, а
получено
выше, а
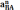 находится
по формуле
находится
по формуле
, м/с2
Для
решения уравнения из произвольно
взятой точки "о" проводим вектор
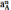 ,
,
с
его конца строим вектор  , а с его конца строим прямую перпендикулярную
к АВ, а точки "о" проводим прямую
параллельную OY
, а с его конца строим прямую перпендикулярную
к АВ, а точки "о" проводим прямую
параллельную OY
Длины
отрезков соответствующие ускорениям
 находят
по следующей формуле
находят
по следующей формуле
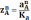 ,
мм
,
мм
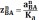 ,
мм
,
мм
где Kа – произвольно взятый масштаб ускорения, м/(с2*мм)
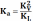
В
полученной точке пересечения прямых
будет точка "b".
Где будут концы векторов изображающие
скорости 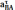 и
и
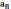 .
.
Численное значение этих ускорений
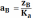
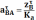
Угловое ускорение 2 звена находится по формуле
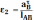 ,
1/c2
,
1/c2
Для
установления направления ε2
и перенесем ускорения 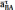 в точку В
и, рассматривая движение В
относительно точек А,
установим, что ε2
направлено против часовой стрелки.
в точку В
и, рассматривая движение В
относительно точек А,
установим, что ε2
направлено против часовой стрелки.
Ускорение точки D находим из уравнений:
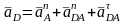
где
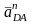
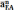 ∥
АВ,
∥
АВ,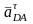
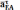 ⏊
АВ
⏊
АВ
Значение
ускорений
,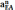
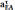 находятся
по формулам:
находятся
по формулам:

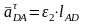
Длины отрезков соответствующие ускорениям , находятся по следующим формулам:
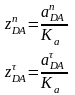
Для
решения уравнения из точки "о"
проводим вектор
,
с его конца строим
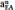 ,
с
его конца строим
,
с
его конца строим
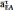 ,
на
его конце получим точку "d".
Сумма всех трёх векторов дает вектор
,
на
его конце получим точку "d".
Сумма всех трёх векторов дает вектор
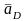
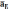 ,
начало
которого в точке "о", а конец в
точке "d".
,
начало
которого в точке "о", а конец в
точке "d".
Для определения ускорения точки C, принадлежащей звену 4 составим уравнение, так как точка С принадлежит звену 4 и 5, то уравнение выглядит следующим образом
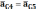
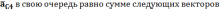
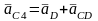
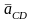
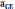 складывается
из нормального
складывается
из нормального
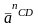
 и тангенсального ускорения
и тангенсального ускорения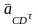 т.е.
т.е.
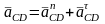
где
СD
,
CD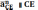
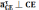
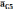 также
двигается по своей окружности и, поэтому
ускорения так же будет иметь нормальную
и тангенсальную составляющую
также
двигается по своей окружности и, поэтому
ускорения так же будет иметь нормальную
и тангенсальную составляющую
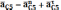
где
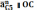
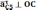
Значение
ускорений
,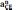
 находятся
по формулам:
находятся
по формулам:
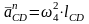 ,
м/с2
,
м/с2
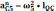 ,
м/с2
,
м/с2
Длины
отрезков, соответствующие ускорениям
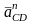 ,
находятся
по следующим формулам:
,
находятся
по следующим формулам:
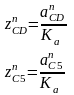
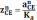
Окончательный вид уравнения будет следующим:
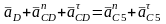
В
этом уравнение неизвестны лишь значения
двух ускорений
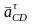
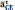 и
и
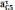 .
.
Для
их
нахоңдения решаем
уравнение графическим способом. Из
точки "а" проводим отрезок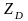
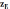 ,
равный
,
равный
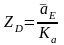
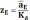 ,
мм., на его конце будет точка "d".
Из точки "d"
откладываем отрезок
,
мм., на его конце будет точка "d".
Из точки "d"
откладываем отрезок
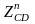
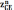 ,
с его конца проводим прямую перпендикулярную
CD.
Далее из точки "о" проводим отрезок
,
с его конца проводим прямую перпендикулярную
CD.
Далее из точки "о" проводим отрезок
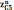 на
его конце проводим прямую перпендикулярную
OC.
В точке пересечения прямых получим
точку С. Полученные отрезки будут
соответствовать длинам ускорений
на
его конце проводим прямую перпендикулярную
OC.
В точке пересечения прямых получим
точку С. Полученные отрезки будут
соответствовать длинам ускорений
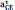 и
и
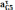
Численное значение и будет равно
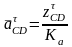
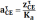 ,
м/с2
,
м/с2
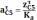 ,
м/с2
,
м/с2
Угловое ускорение 4 и (условно)5 звеньев находятся по формуле:
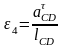
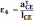
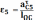 ,
1/c2
,
1/c2
Ускорение точки центра масс второго и четвертого звеньев находятся по следующим формулам
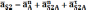
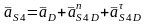
Все части уравнения уже известны.
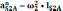 ,
м/с2
,
м/с2
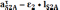
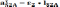 ,
м/с2
,
м/с2
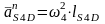

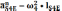 ,
м/с2
,
м/с2
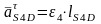 ,
м/с2
,
м/с2
Длины
отрезков, соответствующие ускорениям
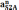
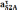
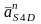
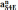
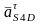
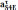 находятся
по следующим формулам
находятся
по следующим формулам
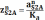 ,
мм
,
мм
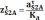 ,
мм
,
мм
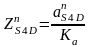 ,
мм
,
мм
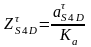 ,
мм
,
мм
Из
точки "а" проводим отрезок 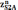 ,
а
с его конца отрезок
,
а
с его конца отрезок 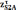 .
На
конце последнего отрезка будет находится
точка s2.
Отрезок os2
будет соответствовать вектору ускорения
.
На
конце последнего отрезка будет находится
точка s2.
Отрезок os2
будет соответствовать вектору ускорения
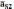 .
Его
численное значение будет равно
.
Его
численное значение будет равно
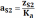 ,
м/с2
,
м/с2
Из
точки "е" проводим отрезок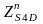
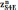 ,
а
с его конца отрезок
,
а
с его конца отрезок
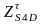
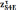 .
На
конце последнего отрезка будет находится
точка s4.
Отрезок os4
будет соответствовать вектору ускорения
.
На
конце последнего отрезка будет находится
точка s4.
Отрезок os4
будет соответствовать вектору ускорения
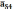 .
Его
численное значение будет равно
.
Его
численное значение будет равно
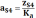 ,
м/с2
,
м/с2
Результаты расчета ускорений для 2 и 6 положения приведены в (Табл.2).
Таблица 2
Результаты расчета ускорений
№ |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
306,25 |
21,23 |
158,09 |
205,75 |
66,3 |
15,5 |
32,46 |
54,86 |
48,92 |
14,82 |
14,1 |
46,37 |
11 |
306,25 |
37.49 |
140,5 |
190,7 |
74.37 |
16.73 |
56.03 |
54,86 |
48,58 |
87,24 |
15,2 |
66,06 |