Министерство образования и науки Российской Федерации
КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
имени А. Н. ТУПОЛЕВА
______________________________________________________________________________________________
Кафедра Машиноведения и инженерной Графики
Расчетно-пояснительная записка к курсовой работе по дисциплине «Теория механизмов и машин»
(Номер задания 2.15)
Выполнил: студент гр.1309
Кильмаков Н.М.
Проверил: профессор Яруллин М.Г.
Казань 2014
Оглавление
1. Исследование шарнирно-рычажного шестизвенного механизма 5
1.1. Исходные данные 5
1.2. Построение кинематической схемы и структурный анализ механизма 5
1.3. Определение скоростей 5
1.4. Определение ускорений 10
1.5. Силовой анализ механизма 16
1.5.1. Определение давлений в шарнирах 16
1.5.2. Определение момента, приложенного к кривошипу 20
1.5.3. Определение момента методом рычага Жуковского 21
2. Исследование эвольвентного зацепления 23
2.1. Исходные данные 23
2.2. Выбор коэффициентов смещения режущего инструмента при помощи блокирующих контуров 23
2.3. Построение картины зацепления 25
3. Исследование планетарных механизмов 27
3.1. Исходные данные 27
3.2. Разбивка общего передаточного отношения по ступеням 27
3.3. Подбор чисел зубьев планетарного механизма 27
3.4. Определение числа сателлитов 28
3.5. Проверка возможности сборки 29
3.6. Кинематический расчет редуктора графоаналитическим методом 29
Исследование шарнирно-рычажного шестизвенного механизма
Исходные данные
LOA=0.25м; LAB=1.0м; LBE=0.15м; LEC=1.1м
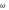1=35
рад/с
Построение кинематической схемы и структурный анализ механизма
Определение скоростей
Величина скорости точки А определяется по формуле
VА = ω1⋅ lОА, м/с,
где lОА = KL ⋅ ОА – длина кривошипа, м; ОА – отрезок на чертеже, изображающий в масштабе KL длину кривошипа, мм; а направление – в соответствии с направлением ω1 (перпендикулярно ОА).
Для определения скорости точки В составим векторное уравнение:
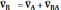
В
этом уравнении известны величина и
направление вектора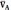 
,
а также направления векторов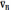 
(
||OY)
и 
(⊥
АВ).
В этом уравнении два неизвестных элемента: величина скорости VB и
VBA. А так как векторное уравнение соответствует двум скалярным, то
указанное уравнение имеет определенное решение. Для определения этих неизвестных строим многоугольник (план) скоростей. По указанному в задании отрезку оа, изображающему на чертеже скорость VA, подсчитываем масштаб скорости:
KV = VA/oa, м/(с⋅мм) (оа =70 мм).
Из произвольно взятой на чертеже точки "о" откладываем отрезок оа
перпендикулярно ОА. Через конец этого отрезка (точку а) проводим прямую перпендикулярно АВ, а через точку "о" – прямую, параллельную OY. Полученная от пересечения этих прямых точка b определяет длины отрезков оb и аb, которые изображают на чертеже скорости VB и VBA. Величины этих скоростей:
VB = ob⋅KV, м/с; VBA = ab⋅KV, м/с.Для определения скорости точки C составим два
уравнения:
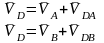
и решим их совместно. Для чего через точку a проведем прямую
перпендикулярно AD и через точку b – прямую перпендикулярно DB.
Пересечение этих прямых определяет точку d, отрезок od и,
следовательно, скорость VD, численное значение которой
VD = od⋅KV, м/с.
Для определения скорости точки C составим векторное уравнение:
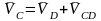
В
этом уравнении известны величина и
направление вектора
,
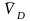
а также направления векторов 
(⊥OC)
и
(⊥
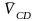
CD).
В этом уравнении два неизвестных элемента: величина скорости VC и VCD. Из точки "d" проводим прямую перпендикулярно СD, а через точку "о" – прямую, перпендикулярную OC. Полученная от пересечения этих прямых точка" c" определяет длины отрезков ос и cd, которые изображают на чертеже скорости VC и VCD. Величины этих скоростей:
VC = oc⋅KV, м/с; VCD = cd⋅KV, м/с.
Скорость точки S4 определяется так: центр тяжести звена 4 находится на середине отрезка DC, из этого мы можем найти положение точки S4 на плане скоростей, она будет находиться на середине отрезка ds. Соединяем точку о и , найденную точку s4, таким образом получаем искомую скорость точки S4.
Величина этой скорости:
VS4 = os4⋅KV, м/с;
Для определения положения точки S2 на плане скоростей составим пропорцию:
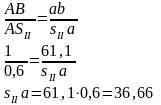
Таким образом нашли положение точки sII на плане скоростей. Значение скорости точки sII равно:
VS2 = os2⋅KV, м/с.
Теперь найдем угловые скорости звеньев.Угловая скорость шатуна 2:
ω2 = VBA / lAB, 1/c,
где lAB = KL⋅ AB – длина шатуна 1м; Угловая скорость шатуна 4:
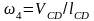1/c,
где lCD = KL⋅ СD – длина шатуна 1.1м;
На примере 9-го положения:
VA=1*LOA =35*0,25=8,75 (м/с)
Kv=VA/oa=8,75/70=0,125 (м/(с*мм))
VB=VA+VB
VB=ob*Kv =27,36*0,125=3,42 (м/с)
VBA=ab*Kv=61,1*0,125=7,64 (м/с)
VD=od*Kv=29,92*0,125=3,74 (м/с)
VDA=ad*Kv=51,94*0,125=6,5 (м/с)
VC=oc*Kv=34,68*0,125=4,335 (м/с)
VCD=cd*Kv=5,79*0,125=0,74 (м/с)
VS4=os4*KV=32,26*0,125=4,04 (м/с)
VS4D=ds4*KV=9.96*0,0714=0,711 (м/с)
VS2 = os2⋅KV=38,9*0,125=4.83 (м/с)
VS2A = as2⋅KV=36,66*0,125=4,58 (м/с)
ω2=VBA/LAB=2.56 /1=2.56 (1/c)
ω4=VCD/LCD=0,73 /1.1=0,66 (1/c)
ω5=VC/LOC=4,335 /0.7=6,2 (1/c)
Результаты расчета скоростей для 12-ти положений приведены в (Табл.1).
Таблица 1
Результаты расчета скоростей:
№ |
Va |
Vb |
Vba |
Vd |
Vda |
Vc |
Vcd |
Vs2 |
Vs4 |
ω2 |
ω4 |
ω5 |
1 |
8,75 |
8,75 |
0 |
8,75 |
0 |
4,956 |
0,064 |
8,75 |
4,978 |
0 |
0,058 |
7,08 |
2 |
8,75 |
8,55 |
4,48 |
8,43 |
3,81 |
6,9 |
2,49 |
8,35 |
7,6 |
4,48 |
2,26 |
9,86 |
3 |
8,75 |
5,33 |
7,64 |
5,31 |
6,5 |
3,6 |
2,79 |
5,8 |
4,32 |
7,64 |
2,54 |
5,15 |
4 |
8,75 |
0 |
8,75 |
0,75 |
4,25 |
0,476 |
0,748 |
2 |
0,507 |
5 |
0,68 |
0,68 |
5 |
8,75 |
6,1 |
7,76 |
5,92 |
6,6 |
8,6 |
4,25 |
6,18 |
7,074 |
7,76 |
3,86 |
6,07 |
6 |
8,75 |
8,55 |
4,48 |
8,43 |
3,81 |
8,26 |
0,33 |
8,35 |
8,34 |
4,48 |
0,3 |
11,8 |
7 |
8,75 |
8,75 |
0 |
8,75 |
0 |
5,34 |
0,538 |
8,75 |
5,166 |
0 |
0,489 |
7,629 |
8 |
8,75 |
6,61 |
4,48 |
6,79 |
3,81 |
8,17 |
1.9 |
7,21 |
7,45 |
4,48 |
1,73 |
11,67 |
9 |
8,75 |
3,42 |
7,64 |
3,74 |
6,5 |
4,335 |
0,74 |
4.83 |
4,04 |
2.56 |
0,66 |
6,2 |
10 |
8,75 |
0 |
8,75 |
0,75 |
4,25 |
0,875 |
1,375 |
2 |
0,437 |
8,75 |
1,25 |
1,25 |
11 |
8,75 |
3,42 |
7,64 |
3,74 |
6,49 |
6,63 |
4,33 |
4,86 |
4,93 |
7,64 |
3,94 |
9,47 |
12 |
8,75 |
6,61 |
4,48 |
6,79 |
3,81 |
8,95 |
2,99 |
7,21 |
7,75 |
4,48 |
2,72 |
12,79 |