Застосування похідної

1. Зростання та спадання функції

Теорема про необхідні та достатні умови зростання та спадання функції на проміжку:

Якщо функція диференційована на і якщо

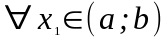• для , то функція на цьому проміжку зростає;

• для , то функція на цьому проміжку спадає.

Схема дослідження функції на монотонність:

1) Знаходимо ;

2) знаходимо похідну;

3) знаходимо критичні точки (точки, в яких похідна дорівнює нулю, або не існує);

4) критичні точки ділять на проміжки монотонності;

З кожного проміжку виберемо довільну точку і підставимо її в похідну. Якщо

• , то функція зростає на цьому проміжку;

• , то функція спадає на цьому проміжку.

2. Екстремуми функції

Основні означення:

Точка називається точкою максимуму функції , якщо для 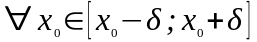виконується умова .

Значення функції в точці максимуму називається максимумом функції і позначається .

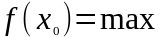Точка називається точкою мінімуму функції , якщо для виконується умова .

Значення функції в точці мінімуму називається мінімумом функції і позначається .

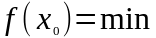Мах і тіn функції називається екстремумом функції.

Необхідна умова існування екстремуму. Теорема Ферма:

Якщо точка екстремуму функції і функція в цій точці має похідну, то .

Достатня умова екстремуму. Теорема Роля:

Якщо при переході через критичну точку похідна неперервної функції змінює знак, то функція в цій точці має екстремум, якщо:

1) з "+" на "-", то - точка максимума;

2) з "-" на "+", то - точка мінімума.

Схема дослідження функції на екстремум:

1. Знаходимо критичні точки першого роду.

2. Розміщуємо критичні точки в порядку зростання. підставляємо в похідну любе число менше , потім більше , але менше . Якщо при цьому знак похідної змінюється з "+" на "-" , то функція при має максимум, якщо з "-" на "+", то функція при має мінімум.

3. Обчислюємо тобто знаходимо максимальне значення функції.

3. Точки перегину

Графік функції , називається опуклим на , якщо графік розміщений нижче будь-якої дотичної, проведеної до графіка функції в точках .

Графік функції , називається вгнутим на , якщо графік розміщений вище будь-якої дотичної, проведеної до графіка функції в точках .

Достатня умова опуклості графіка функції:

Теорема. Якщо функція двічі диференційована на , і для , то графік функції вгнутий, якщо для , то графік функції опуклий.

Необхідна умова існування точка перегину:

Теорема. Якщо функція має неперервні похідні до другого порядку на і являться точкою перегину, то .

Достатня умова існування точка перегину:

Теорема. Якщо функція , двічі диференційована на і при переході через друга похідна змінює знак, то точка кривої з абсцисою являється точкою перегину.

Схема дослідження функції на перегин:

1. Знаходимо критичні точки другого роду.

2. Розміщуємо критичні точки в порядку зростання підставляємо в другу похідну любе число менше , потім більше , але менше . Якщо при цьому друга похідна змінює знак, то при маємо точку перегину.

3. Обчислюємо тобто знаходимо перегин.