48

Міністерство освіти і науки України

Полтавський будівельний технікум транспортного будівництва

Робочий зошит № 5

для практичних занять з навчальної дисципліни

«Математика»

Змістовий модуль 5. Похідна та її застосування

Студента групи ______________

____________________________________

(прізвище, ім’я)

Полтава 2015

Результат виконання роботи

	Практичне заняття № 1	Практичне заняття № 2	Практичне заняття № 3	Практичне заняття № 4	Практичне заняття № 5	Практичне заняття № 6
Оцінка

ЗМІСТ

Змістовий модуль 5. Похідна та її застосування ……………………………..…..5

Опорний конспект теми……………………………………………………………..5

Практичне заняття №1. Обчислення границь…………………………………….19

Практичне заняття № 2. Диференціювання функцій…………………………….24

Практичне заняття № 3. Базові задачі на застосування похідної……………….30

Практичне заняття № 4. Дослідження функції за допомогою похідної та побудова графіку…………………………………………………………………...34

Практичне заняття № 5. Тематичний тест……………………..………………....36

Практичне заняття № 6. Контрольна робота №3…………………………………42

Список використаних та рекомендованих джерел……………………………….45

Змістовий модуль 5. Похідна та її застосування

Опорний конспект теми

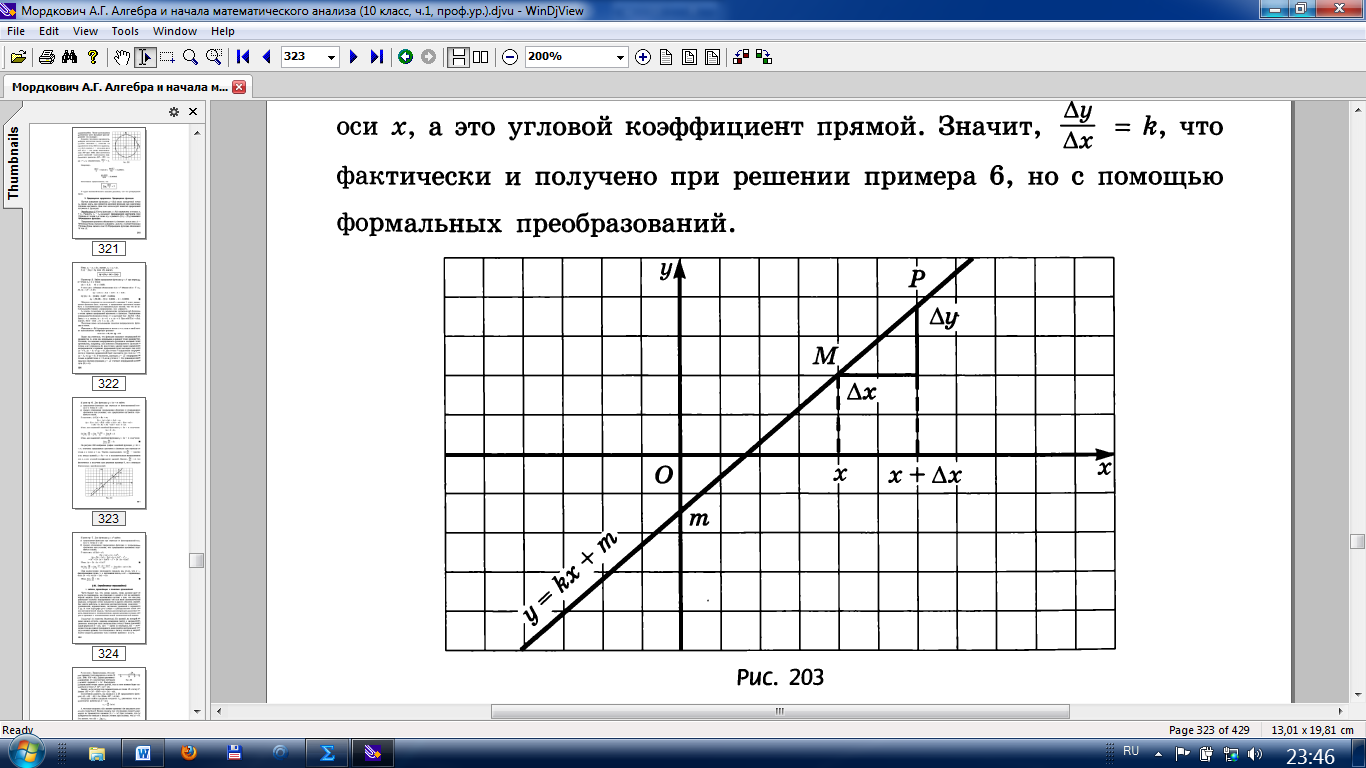
1. Приріст аргументу і приріст функції. Геометрична інтерпретація

Нехай функція 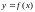визначена в , х₁. Різниця між її значеннями 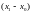називається приростом аргументу і позначається .

Різниця між відповідними значеннями функції називається приростом функції і позначається .

Тобто, , .

= .

У загальному вигляді приріст функції в точці .

Геометрично приріст аргументу відповідає приросту абсциси точки кривої, а приріст функції – приросту ординати цієї точки.

2. Границя функції в точці і на нескінченності

Число А називається границею функції в точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність .

або .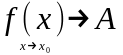

Число А називається границею функції при , якщо для будь-якого існує число , що при всіх .

Функція називається нескінченно малою, якщо .

Функція називається нескінченно великою, якщо .

Якщо - нескінченно мала, то нескінченно велика.

Приклад: Для функції знайти

А) приріст функції при переході від фіксованої точки до точки ;

Б) границю відношення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля.

Розв’язування

А) .

. ;

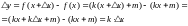
Б)

3. Теорема про границі

Якщо функції і в точці мають границі, то:

1) Границя суми дорівнює сумі границь .

2) Границя добутку дорівнює добутку границь .

Наслідок 1. Постійний множник можна виносити за знак границі .

Наслідок 2. Границя степені дорівнює степені границь .

3) Границя частки дорівнює частці границі , при умові .

₄₎ Границя сталої функції дорівнює цій самій сталій