1. Порядок выполнения работы

Д ля определения постоянной времени  соберите электрическую цепь, состоящую из генератора прямоугольных импульсов ГН-1, омического сопротивления R, индуктивности L и осциллографа.

1. Соберите схему, представленную на рис. 4. С помощью переменного резистора на блоке сопротивлений установить R=100 Ом.

2. Запустите программу «PicoScope», включите цифровой осциллограф.

3. На экране осциллографа получится график зависимости U=f(τ).

4.Установите автоматический диапазон входного сигнала осциллографа (меню ).

5. На панели настройки канала установите режим АС.

6. Нажмите клавишу автоматической установки , на панели захвата изображения, получите оптимальное изображение графика на экране осциллографа.

7. Установите растяжку осциллограммы по горизонтали (меню ) равное 16 и коэффициент развертки (меню ) равное 2^ms/_div (панель настройки канала). Изменяя сопротивление пронаблюдайте на экране зависимость постоянной времени от величины сопротивления R.

8. Определите постоянную времени цепи τ изменяя сопротивление в пределах от 100 до 500 Ом с шагом 100 Ом. Для определения постоянной времени τ необходимо по графику переходного процесса, измерить значение времени, с учетом знака, в начале графика (t₁) и в точке, где U=0,63 U_max (t₂). Для измерения t₁(t₂) подведите курсор и удерживайте левую кнопку мыши в требуемых точках. Полученные значения высвечиваются на экране. Рассчитайте, как τ = t₂ – t_1, результаты измерений занесите в табл. 1 Перед измерением времени остановите обработку данных осциллографом, нажав на панели Запуска/Остановки клавишу .

9. Для получения следующих графиков повторно нажать на панели Запуска/Остановки клавишу .

Таблица 1

R, Ом	10-6, c	(1/)106, c-1
100
200
…

10. Рассчитайте величины 1/ для каждого значения R.

11. Постройте график зависимости 1/= f (R) и убедитесь, что зависимость является линейной.

12. Рассчитайте величину индуктивности L по графику зависимости 1/f(R), где L является величиной, обратной тангенсу угла наклона прямой ,

13. Определите магнитную проницаемость сердечника соленоида, используя формулу (6), при заданных параметров соленоида: S=0.64 см², l=10 мм, N=30.

3. Контрольные вопросы

1. Явление самоиндукции.

2. Потокосцепление при явлении самоиндукции.

3. ЭДС самоиндукции. Индуктивность.

4. Графики зависимости напряжения на резисторе и ЭДС самоиндукции от времени.

5. Постоянная времени цепи  и ее зависимость от параметров контура.

5. Лабораторная работа № 6.21

   1. Вынужденные колебания в последовательном колебательном контуре

Цель работы: изучение явления резонанса в RLC- контуре, определение резонансной частоты и добротности контура.

Приборы и принадлежности: генератор АНР-1002, вольтметр АВ1, стенд СЗ-ЭМ01, соединительные провода.

Краткие теоретические сведения

Последовательный колебательный контур состоит из конденсатора ёмкостью C, соленоида индуктивностью L, омического сопротивления R и источника переменной ЭДС , включенных последовательно (рис. 1).

По закону Ома для неоднородного участка цепи сила тока:

I=( + _s – )/R, (1)

где - ЭДС источника переменного напряжения, которая изменяется по синусоидальному закону =₀sin(t), _s - ЭДС самоиндукции, возникающая в соленоиде,  - разность потенциалов на обкладках конденсатора, которую в дальнейшем будем обозначать через U.

Преобразуя (1), составим дифференциальное уравнение, описывающее колебательный процесс в рассматриваемом контуре

IR =  – LdI/dt – U, (2)

где _s = – LdI/dt,  = U.

Силу тока в цепи I и напряжение на конденсаторе U можно связать, рассматривая процесс изменения заряда конденсатора:

I = dq/dt, U = q/C, I = CdU/dt (3)

Подставив (3) в (2), получим:

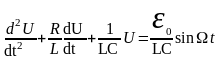(4)

Введём обозначения: R/2L=, 1/CL=₀² и ₀/CL=E₀ (₀ - частота собственных колебаний контура, - коэффициент затухания,  - частота внешней ЭДС). После их подстановки в (4) имеем неоднородное дифференциальное уравнение вынужденных колебаний:

(5)

Решением его является сумма частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения, которым в установившемся режиме колебаний можно пренебречь. Частное решение неоднородного уравнения (5) имеет вид:

U=U₀()sin(t+), (6)

где амплитуда напряжения на конденсаторе U₀ может быть найдена подстановкой (6) в (5). Параметр , представляющий собой сдвиг фаз колебаний напряжения на конденсаторе по отношению к колебаниям вынуждающей ЭДС, в лабораторной работе не определяется.

Г рафик вынужденных колебаний напряжения на конденсаторе (уравнение (6)) представлен на рис. 2. Вынужденные колебания происходят с частотой вынуждающей ЭДС Ω.

При приближении частоты внешнего вынуждающего воздействия Ω к собственной частоте колебаний ω₀ в контуре резко возрастает амплитуда колебаний напряжения на конденсаторе – происходит явление резонанса. В работе исследуется зависимость амплитуды колебаний напряжения на конденсаторе U₀ от Ω при разных сопротивления контура R.

Амплитуда вынужденных колебаний:

(7)

Из формулы (7) видно, что величина U₀ зависит прямо пропорционально от амплитуды вынуждающей ЭДС ε₀ и сложным образом от параметров колебательного контура ₀ и . Исследование зависимости U₀() показывает:

1) при   0 напряжение на конденсаторе U₀  ₀;

2) функция U₀() обладает максимумом при частоте генератора:

(8);

3 ) напряжение на конденсаторе U₀ стремится к нулю при   ∞.

Графики зависимости U₀() для различных коэффициентов затухания  приведены на рис. 3. Данные графики отражают явление резонанса напряжений. Частота вынуждающей ЭДС, при которой U₀=U₀^max, называется резонансной. Она зависит от параметров колебательного контура (формула (8)).

Следует отметить, что резонанс для силы тока наблюдается при частоте ₀, не зависящей от .

Для колебательного контура вводится понятие добротности:

Q_i = U_oi ^max/_o (9)

или: , (10)

где 2- ширина резонансной кривой при _.