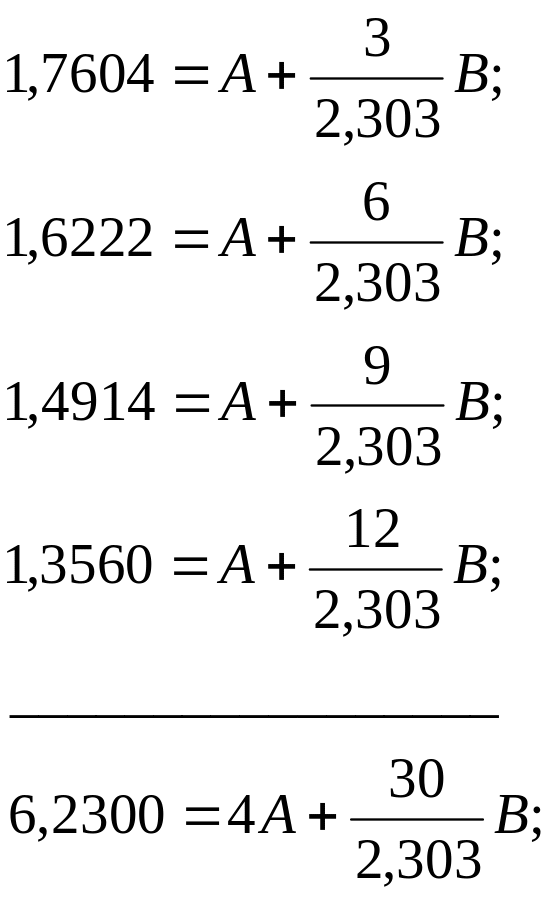0

Міністерство освіти і науки України

Запорізький національний технічний університет

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних робіт

з дисципліни “Основи наукових досліджень”

для студентів спеціальності

6.050403 “Прикладне матеріалознавство”

денної і заочної форм навчання

Частина 2

2010

Методичні вказівки до лабораторних робіт з дисципліни “Основи наукових досліджень” для студентів спеціальності 6.050403 “Прикладне матеріалознавство”, денної і заочної форм навчання. Частина 2 / Укл.: В.С. Вініченко, Д.В. Ткач – Запоріжжя: ЗНТУ, 2010 – 38 с.

Укладачі:	В.С. Вініченко, доцент, к.т.н. Д.В. Ткач, асистент
Рецензент:	В.Я. Грабовський доцент, к.т.н.
Відповідальний за випуск	А.Д. Коваль, професор, д.т.н.

Затверджено радою фізико-технічного інституту Протокол № 4 від 27 травня 2010 р.

Затверджено на засіданні кафедри “Фізичне матеріалознавство” Протокол № 10 від 19 травня 2010 р.

З МІСТ

Частина 2

ЛАБОРАТОРНА РОБОТА №9 ОФОРМЛЕННЯ РЕЗУЛЬТАТІВ НАУКОВОЇ РОБОТИ 91

Лабораторна робота №6 підбір емпіричних формул у вигляді поліному з застосуванням методу середніх квадратів

Мета роботи: опанувати визначення коефіцієнтів поліному методом середніх квадратів.

6.1. Загальні відомості

В техніці часто використовуються сумісні вимірювання, наприклад, для встановлення функції перетворення як залежності між вихідною та вхідною величинами вимірювального пристрою, приладу тощо.

При наближенні експериментальних результатів аналітичними залежностями можливі дві ситуації. Перша, коли з фізичних чи інших міркувань вид залежності між функцією та аргументом є відомим, але невідомі коефіцієнти цієї залежності. Наприклад, відомо, що опір цього металу описується параболічною залежністю від температури, однак коефіцієнти цієї залежності невідомі і їх треба визначити на підставі сумісних вимірювань кількох пар значень температури та опору. У таких задачах не виникає проблеми вибору апроксимаційної функції - її задано апріорі.

В іншій задачі характер залежності між вхідною величиною (аргументом) та вихідною величиною (функцією) може бути не відомим. У такій задачі необхідно спочатку вибрати певну аналітичну модель залежності і на підставі результатів вимірювань знайти параметри цієї моделі.

При проведенні сумісних вимірювань отримують статистичний ряд значень двох величин., коли кожному значенню функції у₁, у₂,..., у_n відповідає певне значення аргументу х_1, х₂, ..., х_n.. Використовуючи такі експериментальні дані можна підібрати алгебраїчні вирази функції

, (6.1)

які називаються емпіричними формулами. Такі формули підбирають лише в межах виміряних значень аргументу х₁-х_n. Такими формулами користуються, якщо (6.1) складний, вимагає складання програм для ЕОМ, або взагалі не має аналітичного виразу. Заміна точних аналітичних виразів наближеними, більш простими називають апроксимацією.

На першому етапі дані наносять на сітку прямокутних координат, з’єднують експериментальні точки плавною кривою і вибирають орієнтовно вид формули (математичної моделі).

На вибір виду моделі найбільшою мірою впливають результати теоретичного та емпіричного вивчення досліджуваного явища, тобто досвід експериментатора. Поштовхом до належного вибору моделі можуть стати результати попереднього опрацювання результатів, наприклад, графічне зображення експериментальних точок у вигляді орієнтовного графіка. Проаналізувавши такий графік, можна встановити також кількість апроксимуючих членів.

При цьому, якщо вибрати кількість апроксимаційних членів замало, наприклад, залежність насправді є квадратною параболою (3 члени і 3 невідомі коефіцієнти), а пробують апроксимувати результати лінійною залежністю (2 члени і 2 невідомі коефіцієнти); виникає систематичне відхилення апроксимуючої функції від експериментальних даних, тим більше, чим більший вміст неврахованих членів у експериментальних даних.

Якщо ж кількість апроксимаційних членів більша, ніж потрібно, то зростає вплив випадкових чинників на значення знайдених коефіцієнтів та самої апроксимуючої функції. Одним з проявів цього є те, що зі збільшенням кількості апроксимаційних членів апроксимуюча функція щораз "краще" відстежує випадкові флуктуації результатів вимірювань. Зокрема, нехай справжня залежність є лінійною, а для визначення оцінок параметрів цієї лінії здійснено вимірювання у чотирьох точках (рис. 6.1). Очевидно, що найкраща апроксимаційна функція у такому разі - пряма лінія (2 члени, т = 2). Якщо спробувати апроксимувати цю залежність параболою (3 члени, т = 3), то вона пройде ближче до експериментальних точок, ніж пряма, а кубічна парабола (4 члени, т = 4) теоретично точно пройде через всі чотири експериментальні точки, тобто така апроксимація повністю вбере в себе всі випадкові зміни результатів вимірювань.

Рисунок 6.1 ‑ Пояснення впливу порядку апроксимаційної функції на якість апроксимації

Тому важливим є використання об'єктивних кількісних показників (критеріїв) адекватності (згідності) вибраної апроксимуючої моделі.

На другому етапі розраховують параметри (коефіцієнти) формули.

При підборі емпіричних формул зручно використовувати поліноми

y =A₀ + А₁х + А₂х² + А₃х³ + ...+ А_n хⁿ (6.2)

де A_0, А_1, А_n – постійні коефіцієнти. Поліномами можна апроксимувати любі результати вимірювань, якщо вони графічно виражаються безперервними функціями. Для визначення коефіцієнтів А застосовують метод середніх квадратів, або метод найменших квадратів. Метод середніх завдяки своїй простоті дозволяє у більшості випадків замінити громіздкий метод найменших квадратів і одержати достатньо задовільні за точністю результати.

Метод середніх квадратів базується на наступному положенні. По експериментальним точкам можна побудувати декілька плавних кривих. Найкращою буде та крива для якої різниці відхилення виявляться найменшими, тобто . Порядок розрахунку коефіцієнтів здійснюють наступним чином. Визначають число членів ряду (6.2), яке зазвичай приймають не більше 3...4. В прийнятий вираз послідовно підставляють координати х і у декількох експериментальних точок і отримують систему із m рівнянь. Кожне рівняння прирівнюють відповідному відхиленню.

A₀ + А₁х + А₂х² + А₃х³ + ...+ А_n хⁿ – у₁ = ₁

A₀ + А₁х + А₂х² + А₃х³ + ...+ А_n хⁿ – у₂ = ₂ ; (6.3)

.........................................................................

A₀ + А₁х_m + А₂х_m² + А₃х³ + ...+ А_n х_mⁿ – у_m = _m.

Число точок, тобто число рівнянь повинно бути не менше числа коефіцієнтів А, що дозволить їх розрахувати шляхом розв’язання системи (6.3). Для цього систему початкових рівнянь (6.3) послідовно зверху вниз ділять на групи, число яких повинно дорівнювати кількості коефіцієнтів. В кожній групі рівняння підсумовують і отримують нову систему рівнянь, кількість яких дорівнює кількості груп (як правило 2...3). Розв’язування системи дозволяє розрахувати значення коефіцієнтів А.

Метод середніх квадратів має високу точність, якщо кількість точок не менше 3...4.

Приклад 6.1. Виконано сім вимірювань:

4	5	6	7	8	9	10
10,2	6,7	4,8	3,6	2,7	2,1	1,7

Для підбору емпіричної формули вибрано поліном

(6.4)

Підстановкою значень вимірювань в це рівняння отримаємо систему початкових рівнянь

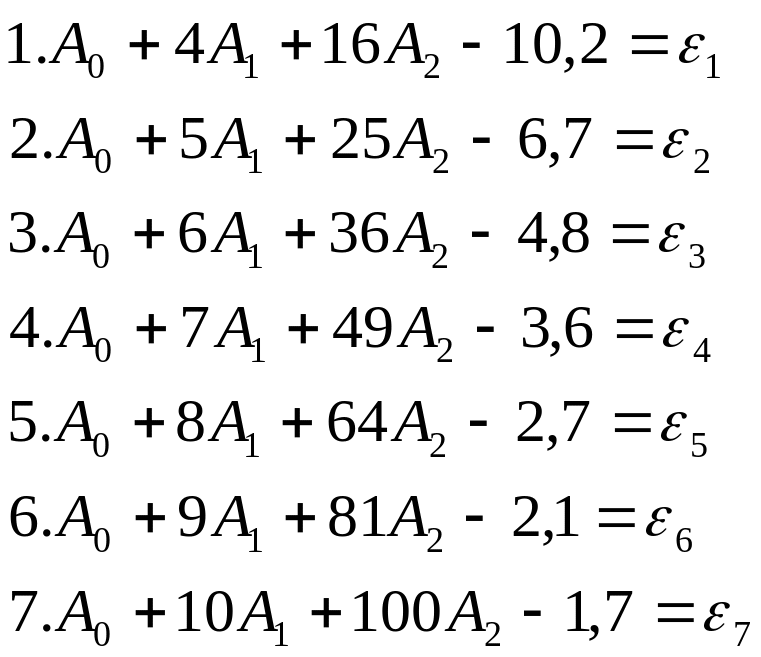
Їх можна розділити на три групи 1...2, 3...4, 5...7. Підсумовування рівнянь в кожній підгрупі дає

1 група 2А₀ + 9А₁ +41А₂ = 16,9;

2 група 2А₀ + 13А₁ + 85А₂ = 8,4;

3 група 3А₀ + 27А₁ + 24А₂ = 6,5.

Визначення з цих рівнянь значень А₀, А₁, А₂ приводить до емпіричної формули

.

Метод середніх квадратів може бути застосовано для кривих після їх вирівнювання.

Приклад 6.2. Маємо вісім сумісних вимірювань

3	6	9	12	15	18	21	24
57,6	41,9	31,0	22,7	16,6	12,2	8,9	6,5

Аналіз цих вимірювань в системі прямокутних координат дає можливість застосувати формулу

(6.5)

Виконаємо вирівнювання заміною змінних

, .

Тоді ,

де , .

Так як необхідно визначити два параметри, то всі виміри ділять на дві групи по чотири вимірювання. Це дає наступні рівняння

Після підсумовування отримано систему з двох рівнянь з двома невідомими А і В рішення якої дає:

; ; ; .

Кінцевий результат має форму .