7. Смещению изображения на комплексной плоскости на комплексное число соответствует умножение оригинала на (теорема смещения):
8. Умножению
аргумента оригинала на постоянное число
соответствует
деление аргумента изображения и самого
изображения на это же число (теорема
изменения масштаба, теорема подобия):
9. Если изображение может быть представлено в виде отношения двух полиномов от p, не имеющих общих корней
причем
степень полинома
выше, чем степень полинома
,
а уравнение
не имеет кратных корней, то для перехода
от изображения к оригиналу можно
воспользоваться теоремой
разложения:
где
—корни
уравнения
Если
в уравнении
один корень равен нулю, то полином
можно представить в виде
,
а оригинал находят по формуле
(3.2)
Если
среди m
корней уравнения
имеется n
— вещественных
и
—
комплексных, то обозначив вещественные
корни через
(k=1,
2, … , n),
а комплексные — через
и положив
тогда
(3.3)
Теорема
разложения в сочетании с другими
свойствами преобразования Лапласа дает
возможность составить таблицы
оригиналов и изображений,
значительно облегчающие и ускоряющие
расчеты переходных процессов. Следует
отметить, что в ряде справочников
приведены таблицы преобразований
Лапласа–Карсона
которое отличается от преобразования
Лапласа только наличием множителя p.
6.2.2.Уравнения электрического равновесия цепи в операторной форме
При использовании преобразования Лапласа, каждому уравнению, входящему в систему уравнений электрического равновесия цепи, можно поставить в соответствие уравнение, составленное относительно операторных изображений токов и напряжений.
Вследствие
того, что изображение суммы функций
времени равно сумме изображений этих
функций, то для перехода от уравнений
баланса мгновенных значений токов и
напряжений ветвей к уравнениям баланса
операторных изображений токов и
напряжений достаточно заменить мгновенные
значения токов и напряжений их операторными
изображениями, т.е. первый закон Кирхгофа
в операторной форме
Если уравнения баланса напряжений формировались относительно мгновенных значений напряжений отдельных элементов, то в операторной форме уравнение второго закона Кирхгофа принимает вид
Эти уравнения будем называть уравнениями баланса токов и напряжений в операторной форме, а операторные изображения токов и напряжений — операторными токами и напряжениями.
аналогии
с рассмотренными ранее понятиями
комплексного входного сопротивления
и комплексной входной проводимости
вводят понятия операторного входного
сопротивления
и операторной входной проводимости
-
Операторным входным сопротивлением пассивного линейного двухполюсника называется отношение операторного напряжения на входе двухполюсника к операторному току при нулевых начальных условиях:
где
и
— операторные изображения тока и
напряжения на зажимах двухполюсника
при
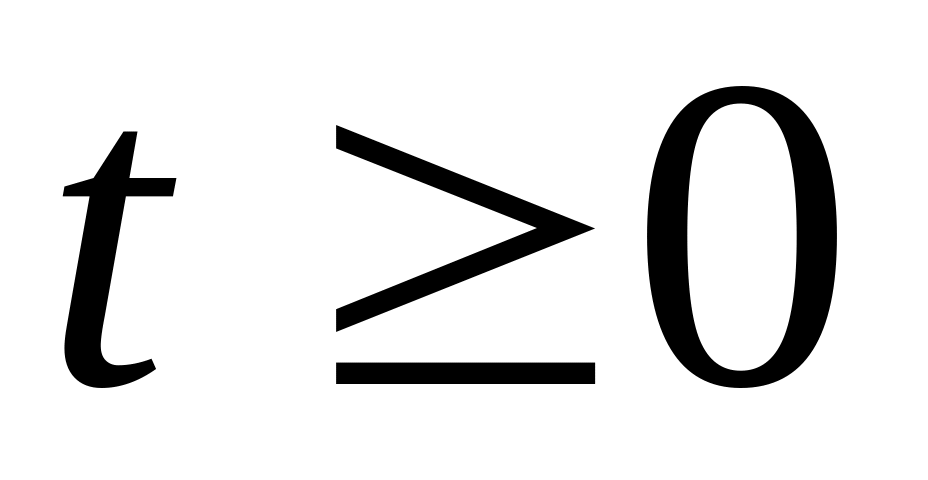и
нулевых начальных условиях
[1] .Величина, обратная , называется операторной входной проводимостью
