7.1.4.Расчет переходных процессов в цепях с синусоидальными источниками классическим методом

Пусть для цепи (рис. 6.13) дано: .

Определить:

Начальные условия при :

;

.

Определим эти токи комплексным Рис.6.13 методом по схеме замещения (рис. 6.14):

.

Тогда при токи равны:

.

Напряжение на конденсаторе:

.

При t = 0_-

.

По закону коммутации:

.

При t = 0₊ составим схему замещения (рис. 6.15), где .

Рис. 6.14

Составим уравнения процессов в цепи по законам Кирхгофа:

После решения этих уравнений получим:

; ; .

Рис. 6.15 Рис. 6.16

При t >>0 определим принужденные составляющие: .

Для этого составим схему замещения (рис. 6.16). Комплексным методом определим токи и переведем их во временную область:

;

;

.

Находим корень характеристического уравнения. Для этого оьносительно источника находим входное сопротивление.

После преобразований получаем

,

тогда корень характеристического уравнения равен: .

Решение для первого тока:

.

Постоянную интегрирования А найдем при :

;

.

Решение для второго тока аналогично:

;

.

Третий ток найдем по первому закону Кирхгофа:

.

6.1.5.Порядок анализа переходных процессов классическим методом

В общем случае расчет переходных процессов классическим методом осуществляется в следующем порядке.

1. Анализ цепи до коммутации В результате этого анализа определяют токи в индуктивностях и напряжения на емкостях в момент времени, непосредственно предшествующий коммутации ( ).

2. Определение независимых начальных условий. Независимые начальные условия представл Ияют собой токи в индуктивностях и напряжения на емкостях в момент времени . Независимые начальные условия находятся с помощью законов коммутации или принципов непрерывности потокосцепления и электрического заряда.

3. Анализ установившегося процесса в цепи после коммутации. В результате анализа установившегося процесса в цепи после коммутации находится принужденная составляющая реакции цепи (частное решение дифференциального уравнения цепи).

4. Определение свободной составляющей реакции цепи. На этом этапе составляе тся характеристическое уравнение цепи. Находятся его корни, и определяется общий вид свободной составляющей реакции цепи (общее решение линейного однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации).

5. Нахождение общего вида реакции цепи. Находится путем суммирования свободной и принужденной составляющих цепи.

6. Определение постоянных интегрирования. Постоянные интегрирования находятся по зависимым начальным условиям.

7. Окончательная запись реакции цепи.

6.2. Операторный метод анализа переходных процессов Применение преобразования Лапласа к решению дифференциальных уравнений

Необходимость определения постоянных интегрирования из начальных условий в ряде случаев значительно усложняет расчет переходных процессов классическим методом решения линейных дифференциальных уравнений, описывающих исследуемые процессы. По мере усложнения электрических схем и возрастания порядка дифференциальных уравнений трудности, связанные с нахождением постоянных интегрирования, возрастают.

Для инженерной практики более удобным является метод решения линейных дифференциальных уравнений, при котором заданные начальные условия включаются в исходные уравнения и для нахождения искомой функции не требуется дополнительного определения постоянных интегрирования.

Идея этого метода заключается в том, что из области функции действительного переменного решение переносится в область функции комплексного переменного где операции принимают более простой вид. А именно: вместо исходных дифференциальных или интегро-дифференциальных уравнений получаются алгебраические уравнения, затем, производится обратный переход в область функций действительного переменного.

Взаимное соответствие между функцией времени (оригиналом) и ее изображением в операторном методе устанавливается с помощью прямого

и обратного 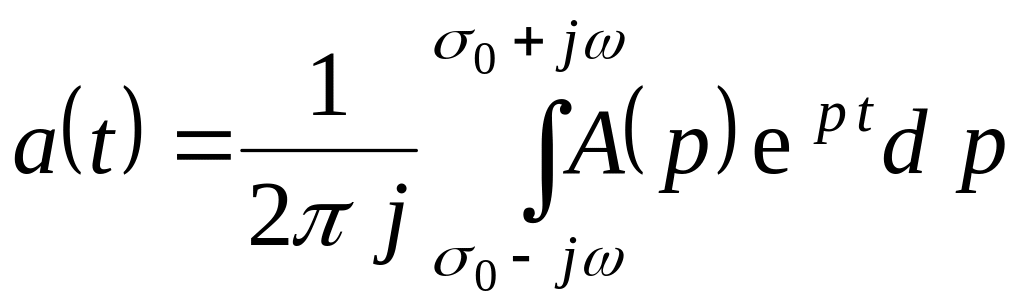преобразований Лапласа и указывается знаком соответствия: 

Функция называется операторным изображением функции или изображением функции по Лапласу. Исходная функция времени по отношению к своему операторному изображению является оригиналом. Комплексное число p будем называть оператором преобразования Лапласа или комплексной частотой.

Некоторые свойства преобразования Лапласа.

1. Изображение по Лапласу постоянной величины K равно этой величине, деленной на p:

2. Умножение функции времени на постоянное число K соответствует умножение на это же число ее изображения:

3. Изображение суммы функций времени равно сумме изображений этих функций:

где

4. Если начальное значение функции равно нулю: то дифференцированию функции соответствует умножение изображения этой функции на p (теорема дифференцирования):

При

5. Интегрированию функции времени в пределах от 0 до t соответствует деление изображения этой функции на p (теорема интегрирования):

6. Смещению функции времени на t₀ соответствует деление изображения этой функции на p (теорема запаздывания):