1 Мысалды шешу нәтижелері

Интервал нөмірі, I	Интервал шегі	Интервал ортасы,	Жиілік , ni	Жинақталған жиілік,	Салыст. Жиілік,	Жинақт. салыст. жиілік,
1	10-12	11	2	2	0,0364	0,0364
2	12-14	13	4	6	0,0727	0,1091
3	14-16	15	8	14	0,1455	0,2546
4	16-18	17	12	26	0,2182	0,4728
5	18-20	19	16	42	0,2909	0,7637
6	20-22	21	10	52	0,1818	0,9455
7	22-24	23	3	55	0,0545	1,0000

2 Сурет – 1 мысалдың мәліметтері үшін гистограмма және огива кездейсоқ шамалардың негізгі статистикалық сипаттамалары

Генеральды жиынтықты бірнеше сандық көрсеткіштермен сипаттау жиі қажет болып тұрады. Таңдама бойынша осы таңдама сипаттамалар (статистикалық сипаттамалар) деп аталатын сипатамалардың жуықталған мәндерін (бағаларын) анықтауға болады.

1. Кездейсоқ шаманың орташа мәні (немесе М)

Қалып сипаттамасы болып табылады. Сандық осьтің қай жерінде зерттелетін таңдама жатқанын көрсетеді. Бұл кездейсоқ шаманың барлық мүмкін болатын мәндері топтасатын жуықталған шама.

2. Дисперсия – кездейсоқ шаманың шашырау сипаттамасы, оның орташа мәнге қатысты шашырауы:

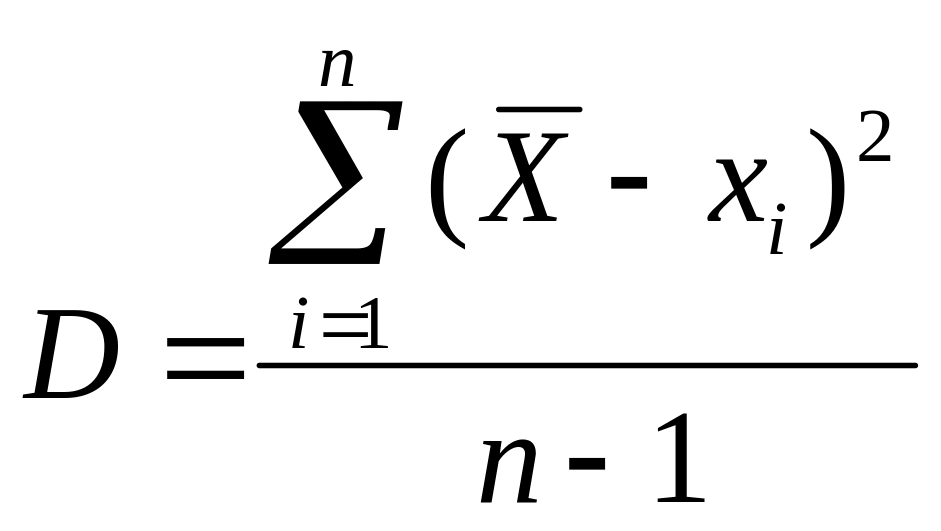
Дисперсия өлшемі х өлшенетін шаманың квадрат бірлігінде алынады.

3. Кездейсоқ шаманың қалыпты бірліктерде шашырауын анықтау үшін орташа квадраттық ауытқу (стандартты ауытқу) шамасы қолданылады.:

4. Мода (Мо) – кездейсоқ шаманың ең жиі кездесетін мәні

11 12 12 13 13 13 14 14 15 16 16

5. Медиана (Ме) – таңдаманы қақ ортасынан бөлетін кездейсоқ шаманың мәні. Барлық мәндерді ранжрленген қатарға орналастыру керек.

25 28 32 34 38 42 45 47 50

Таңдаманың 50% жоғары не төмен орналасқан мәнді көрсетеді.

6. Минимал мәні

7. Максимал мәні

8. Қадам

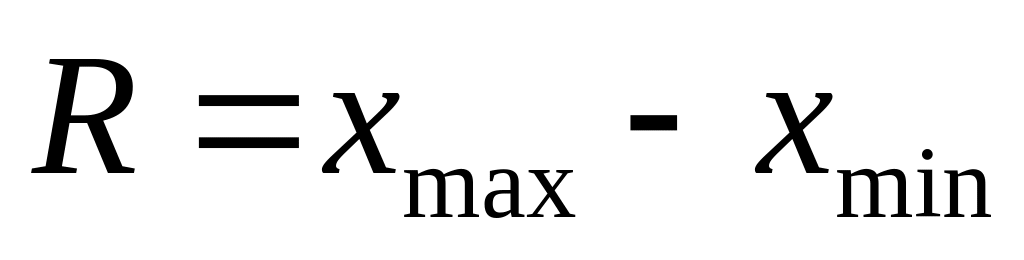
9. Орташа қатесі (стандартты) – таңдама көрсеткіштің (статистика) оның генеральды параметрінен ауытқу шамасы:

Сенімділік интервалы

Белгілі нүктелік таңдама сипаттамалар бойынша интервалды баға немесе сенімділік интервалын құруға болады, онда қандай да бір ықтималдықпен генеральды параметр орналасады. Белгілі таңдама көрсеткіштер негізіндегі генеральды параметрлер туралы сенімді түрде айтуға келетін болып есептелген ықтималдықтар сенімді деп аталады. Әдетте медициналық-биологиялық зерттеулерде Р=0,95 (95%) сенімділік ықтималдығының мәні қолданылады. Және де параметрдің нақты мәнінің осы шектерден шығу ықтималдығы 1–0,95=0,05 (5%)-тен аспайды. Сенімділік ықтималдықты толықтыратын шаманы әдетте α деп белгілейді.

Орталық шекті теоремадан білетініміздей, таңдамалар алынған бастапқы жиынтықтың тарамдалуына тәуелсіз таңдама орташалар жуықтап алғанда қалыпты тарамдалуға ие. Осылайша, таңдама орташа мән үшін сенімділік интервалы және мәндерінің арасында орналасқан, мұндағы m_x орташаның стандартты қатесі, t_α – Стьюдент коэффициенті, п таңдама көлеміне тәуелді (немесе сәйкес f бостандық дәрежелірінің саны) шама және сенімділік ықтималдығының таңдалған деңгейіне тәуелді шама Стьюдент тарамдалу кестелері бойынша анықталады. t_α коэффициент шамасы сенімділік ықтималдығын 1-ге дейін толықтыратын α деңгейінде кесте бойынша анықталады, яғни сенімділік ықтималдығы 95% жағдайда интервал симметриясы ескерілгенде (1-0,95)=0,05 деңгейінде.