Задача 7

Гидравлический расчет вытяжной дымовой трубы.

Функцией вытяжной трубы является создание потока воздуха из здания через топку котла и т.п. в атмосферу. Устойчивый поток воздуха в трубе возникает под действием двух естественных побудительных факторов:

- при обдувании ветром оголовка трубы в выходном сечении возникает локальное понижение давления, при этом давление внутри здания может оказаться достаточным для создания потока воздуха из здания в атмосферу в условиях изотермического процесса, т.е. когда котел не топится;

- если котел топится и труба заполнена (дымом), температура которого выше, чем в атмосфере (а плотность соответственно меньше), то согласно закону Архимеда теплый воздух «вытесняется» вверх.

Так как в процессе розжига котла дым также не должен поступать внутрь помещения, то расчет производится на 2 случая:

1. Котел не топится, но задвижка на трубе открыта (момент растопки котла):

2. Котел топится.

Рис. 10

Дано: труба металлическая диаметром d_т, шероховатость стенок трубы Δ, коэффициент местного сопротивления одного поворота ζ_п. температура воздуха внутри и вне помещения в момент розжига котла t_в, °С. Температура нагретого воздуха на входе в трубу при работе котла t_т, °С.

Оголовок трубы снабжен колпаком. Среднемноголетнее значение скорости ветра v_в (м/с). Общая длина трубы l_т, м. Заданы также возвышения сечений 1-1 и 2-2 над плоскостью сравнения (Z₁ и Z₂).

Требуется: определить расход воздуха (при работе котла-дыма) для двух случаев:

1. Котел не топится, но задвижка на трубе открыта.

2. Котел топится.

Таблица 10

№ Вар.
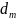
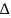
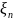
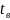
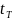
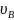
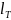
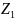
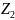
-	мм	мм	-	0С	0С	м/с	м	м	м
1	150	0,8	0,8	0	340	3,5	12	1,5	9,1
2	200	1,0	0,8	0	320	2,8	15	1,8	12,0
3	250	1,0	0,8	0	300	2,5	17	2,0	12,5
4	150	1,0	0,9	10	360	3,0	13	1,4	10,2
5	200	0,8	0,9	10	380	4,0	14	1,7	8,5
6	250	1,5	0,9	10	400	4,5	16	2,1	9,5
7	150	1,5	1,0	20	410	5,0	11	1,5	8,0
8	200	0,8	1,0	20	420	2,6	13	1,7	8,5
9	250	1,5	1,0	20	430	3,0	16	2,0	12,0
10	150	0,9	1,1	5	440	4,0	12	1,4	8,1
11	200	1,2	1,1	5	450	5,0	13	1,6	9,0
12	250	1,2	1,1	5	460	3,2	17	2,1	13,0
13	150	1,0	1,2	15	330	4,1	13	1,3	10,2
14	200	1,2	1,2	15	370	5,1	14	1,5	10,5
15	250	0,8	1,2	15	390	3,6	15	1,7	9,7
16	150	1,1	0,85	0	320	4,2	14	1,3	9,1
17	200	0,9	0,85	0	340	5,2	15	1,5	10,1
18	250	0,9	0,85	0	360	3,0	16	1,6	11,5
19	150	1,4	0,95	10	380	4,0	12	1,4	8,3
20	200	1,4	0,95	10	400	5,0	14	1,5	9,3
21	250	1,4	0,95	10	410	3,1	16	1,4	10,3
22	150	1,3	1,15	15	420	4,1	13	1,5	9,5
23	200	1,3	1,15	15	430	5,1	15	1,4	10,5
24	250	1,3	1,15	15	440	2,6	17	1,5	11,5
25	150	0,9	1,3	0	370	5,5	12	1,3	8,7

- температура воздуха внутри и вне помещения, когда котел не топится.

- температура воздуха на входе в трубу при работе котла.

Указания к решению задачи № 7.

1^й случай. Котел не топится, но задвижка на трубе открыта.

1. Запишем уравнение Бернулли для сечений 1-1 и 2-2, показанных на рис. 10, полагая, что температура воздуха, а следовательно, и его плотность в помещении и вне его одинаковы:

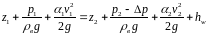3333\* MERGEFORMAT ()

где Р₁ и Р₂ – атмосферное давление на высоте Z₁ и Z₂;

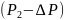– давление в сечении 2-2; – скорость потока воздуха в трубе; общие потери напора от сечения 1-1 до сечения 2-2.

2. Учитывая, что напоры в сечениях 1-1 и 2-2 (при отсутствия ветра) одинаковы 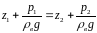, а также сказанное выше, из 33 получаем следующее выражение

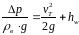3434\* MERGEFORMAT ()

3. Локальное понижение давления относительно атмосферного давления в окрестности выходного сечения трубы определяется по зависимости:

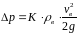3535\* MERGEFORMAT ()

где К – коэффициент, значения которого зависят от конструкции оголовка и находятся по графику, представленному в приложении 4 (конструкция выбирается студентом самостоятельно).

4. Потери напора в трубе вычисляются по формуле:

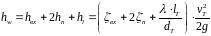3636\* MERGEFORMAT ()

где h_вх - потери напора на входе в трубу;

h_п - потери напора на повороте трубы; λ - коэффициент гидравлического трения трубы; ζ_п - коэффициент местного сопротивления на вход в трубу, принимаемый равный 0,5.

5. В 1^ом приближении коэффициент гидравлического трения 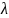определяем по формуле:

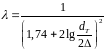3737\* MERGEFORMAT ()

6. Определяем сумму коэффициентов местных сопротивлений

3838\* MERGEFORMAT ()

7. По графику Приложения 4 для выбранного типа оголовка определяем коэффициент “K”.

8. Подставляя в формулу 34 вместо Δp и h_w их выражения по 35 и 36, получим расчетную зависимость для определения скорости движения воздуха в трубе:

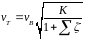3939\* MERGEFORMAT ()

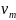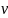9. Используя полученное значение и данные по величине коэффициента кинематической вязкости воздуха при температуре уточняем величину коэффициента гидравлического трения

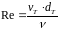4040\* MERGEFORMAT ()

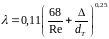4141\* MERGEFORMAT ()

10. По формуле 39 находим уточненное значение скорости воздуха в трубе.

11. Вычисляем расход воздуха в трубе

4242\* MERGEFORMAT ()

где - площадь живого сечения трубы.

2^й расчетный случай. Котел топится.

Труба заполнена горячим воздухом (дымом), плотность которого меньше плотности атмосферного воздуха. Температура горячего воздуха t_т задана.

1. Запишем уравнение Бернулли для потока воздуха в трубе, выбрав сечения 1-1 и 2-2 и плоскость сравнения 0-0, как показано на рис. 10. Так как скорость нагретого воздуха в трубе соизмерима, а зачастую и превосходит скорость ветра, то эффективность побуждающего фактора, связанного с обдуванием оголовка трубы в штатном режиме ее работы (т.е. когда котел топится) невелика и его на этой стадии не учитывают.

4343\* MERGEFORMAT ()

где потеря напора

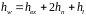4444\* MERGEFORMAT ()

где

; ; .

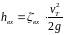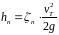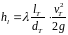2. С учетом сказанного перепишем уравнение 43 в следующем виде:

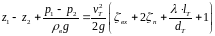4545\* MERGEFORMAT ()

3. Определим разность давлений (p₁ – p₂), предполагая, что распределение давления в атмосфере и внутри здания (вне трубы) подчиняется гидростатическому закону, т.е.

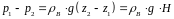4646\* MERGEFORMAT ()

4. Подставим в 43 вместо (p₁ – p₂) его выражение по 46, а вместо 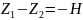, получим следующую расчетную зависимость для вычисления

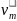
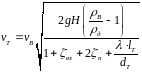4747\* MERGEFORMAT ()

5. Так как нам неизвестна область гидравлического сопротивления трубы, то в 1^ом приближении определяем по формуле

4848\* MERGEFORMAT ()

6. Плотность воздуха при температурах и 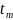определяем по таблице Приложения 5.

7. Подставляя все заданные и найденные величины в правую часть формулы 47, находим .

8. Уточняем коэффициент гидравлического трения , для чего прежде всего используя таблицу приложения 1 устанавливаем область гидравлического сопротивления трубы. При этом ; принимается по таблице приложения 1.

9. По формуле 47 вычисляем уточненное значение скорости горячего воздуха (дыма) в трубе.

10. Определяем расход воздуха в трубе

4949\* MERGEFORMAT ()

Задача № 8

Дано: канал симметричного трапецеидального сечения, заложение откосов «m», ширина канала по дну «b», коэффициент шероховатости стенок «n», уклон дна канала «i» и расход «Q».

Требуется найти глубину наполнения канала «h», если движение в нем равномерное.

Рис. 11

Таблица 11.

№ Вар.	Q м3/с	m	n	в, м
1	40	2.5	0.025	8.6	0.000078
2	40	2.5	0.025	8,6	0,041687
3	28	2,5	0,025	7,5	0,000085
4	28	2,5	0,025	7,5	0,046074
5	18,8	2,5	0,025	6,4	0,000100
6	18,8	2,5	0,025	6,4	0,054107
7	11,5	2,5	0,025	5,2	0,000068
8	11,5	2,5	0,025	5,2	0,078360
9	6,2	2,5	0,025	4,2	0,000072
10	6,2	2,5	0,025	4,2	0,082893
11	31,6	2,0	0,022	6,9	0,000062
12	31,6	2,0	0,022	6,9	0,031199
13	22,4	2,0	0,022	6,0	0,000070
14	22,4	2,0	0,022	6,0	0,035326
15	15,0	2,0	0,022	5,1	0,000081
16	15,0	2,0	0,022	5,1	0,041343
17	9,0	2,0	0,022	4,2	0,000052
18	9,0	2,0	0,022	4,2	0,055354
19	4,8	2,0	0,022	3,3	0,000056
20	4,8	2,0	0,022	3,3	0,059690
21	10,0	2,2	0,018	4,5	0,000120
22	10,0	2,2	0,018	4,5	0,062180
23	30,0	2,2	0,018	6,5	0,000105
24	30,0	2,2	0,018	6,5	0,051430
25	18,0	2,2	0,018	5,5	0,057250

Указания к решению задачи № 8

1. Находим модуль расхода, которым должен характеризоваться рассчитываемый канал. Этот модуль называется необходимым и обозначается К_необх..

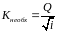5050\* MERGEFORMAT ()

2. Составляем таблицу 12, в которой задаемся рядом значений h и для каждого h вычисляем соответствующий модуль расхода К.

3. По данным 1^ой и 10^ой строк таблицы строим график 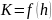(рис.12).

4. По этому графику, зная К_необх., находим искомое h, как показано на чертеже. Кривая имеет выпуклость обращенную в сторону оси h и проходит через начало координат (т.к. при h=0; К=0).

Таблица 12

№ Стро-ки	Величина или расчетная формула	Едини-ца измере-ния	Задаваемые и находимые численные значения					Приме-чание
1	h	м	h1	h2	h3	….	….
2	mh	м						m =
3	b + mh	м						b =
4		м2
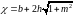
5		м
6		м
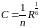
7								n=
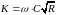
8		м3/с

Рис. 12