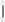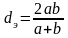Задача № 5

Вода в количестве Q л/с забирается насосом из берегового колодца А, который соединен с водоемом Б самотечной трубой длиной и диаметром d_c (рис. 7). Длина всасывающей трубы l_вс = l₁ + l₂, ее диаметр d_вс. Средняя высота выступов на внутренней поверхности стенок труб (шероховатость) Δ_с=0,5 мм; Δ_вс= 0,25 мм. Коэффициент местного сопротивления сетки самотечной трубы ζ_с=5; коэффициент местного сопротивления на выход из самотечной трубы ζ_вых=1; сетки с обратным клапаном всасывающей трубы ζ_кл=3, колена всасывающей трубы ζ_к=0,3.допускаемый вакуум в трубопроводе перед входом в насос h_вак=6,8 м.

Определить максимально допустимую высоту расположения оси насоса над уровнем воды в колодце h_н, разность уровней воды в водоеме и в колодце z.

Построить напорную и пьезометрическую линии для самотечной трубы.

Примечание: 1) скоростями движения воды в сечениях на свободной поверхности воды в водоеме и в колодце следует пренебречь. 2) t = 10^оС.

Рис. 7.

Таблица 5

№ Варианта	Q, л/с	, м	, мм	, м	, мм
1	4,0	40	75	8,5	50
2	6,0	65	100	9,0	75
3	10,0	50	125	10,0	100
4	7,5	75	100	9,2	75
5	8,5	60	150	9,5	100
6	10,0	55	175	10,5	125
7	9,5	58	125	10,0	100
8	6,5	62	100	8,8	75
9	9,0	55	100	9,8	125
10	7,0	64	100	9,3	75
11	5,0	45	75	8,5	60
12	6,5	50	100	9,0	75
131	9,5	55	125	9,2	100
4	8,5	58	125	10,0	75
15	6,0	60	100	9,5	75
16	4,0	50	75	10,5	50
17	5,5	60	75	10,0	60
18	10,0	55	150	12,0	125
19	9,5	50	125	11,0	100
20	6,5	60	100	9,3	75
21	9,0	50	125	9,5	100
22	7,0	62	100	10,0	75
23	5,0	44	75	9,8	75
24	6,5	55	100	8,5	100
25	5,5	50	75	10,5	50

Указание к решению задачи 5

Чтобы определить превышение уровня в береговом колодце А над уровнем в водоеме Б следует составить уравнение Бернулли для двух сечений потока: сечения 1 – 1 на поверхности воды в водоёме и сечения 2 – 2 на поверхности воды в береговом колодце. Плоскость сравнения провести по уровню воды в береговом колодце, т.е. по сечению 2 – 2;

1414\* MERGEFORMAT ()

; ;

; .

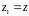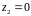т.к. по условию задачи и .

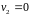После проведенного анализа членов уравнения, получим следующее уравнение

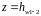1515\* MERGEFORMAT ()

где – потери напора при движении воды по самотечной трубе.

Так как самотечная и всасывающая труба рассматриваются как короткий трубопровод, то при их расчете учитываются оба вида потерь напора: местные и по длине.

1616\* MERGEFORMAT ()

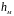где – потери напора в местных сопротивлениях, которые вычисляются по формуле Вейсбаха.

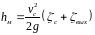1717\* MERGEFORMAT ()

Потери напора по длине за счет трения жидкости о стенки трубы определяются по формуле Вейсбаха-Дарси

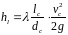1818\* MERGEFORMAT ()

где λ - коэффициент гидравлического трения;

l_c - длина самотечного трубопровода;

d_c - диаметр самотечного трубопровода.

Коэффициент λ может быть определен по формуле А. Д. Альтшуля.

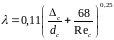1919\* MERGEFORMAT ()

где 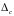- шероховатость самотечной трубы;

Re_c - число Рейнольдса на участке самотечной трубы

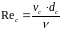2020\* MERGEFORMAT ()

где – кинематический коэффициент вязкости (для t = 10 ⁰С,  = 0,0131 см²/с).

Подставив значения и в расчетные зависимости 16 и 15 определим разность уровней воды в водоеме и в береговом колодце.

Для определения высоты расположения насоса над уровнем воды в береговом колодце следует составить уравнение Бернулли для сечений 2 – 2 на поверхности воды в береговом колодце и n – n перед насосом. Плоскость сравнения провести по уровню воды в береговом колодце, т. е. по сечению 2 – 2.

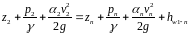2121\* MERGEFORMAT ()

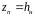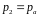; ; ; – по условию задачи; - скорость движения воды во всасывающей трубе; принимается равным 1,0.

2222\* MERGEFORMAT ()

Подставим в уравнение 21 все известные величины

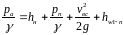2323\* MERGEFORMAT ()

Переписав в левую часть 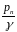, мы получим величину вакуума в сечении n – n

2424\* MERGEFORMAT ()

Таким образом, окончательно расчетное выражение будет иметь вид:

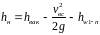2525\* MERGEFORMAT ()

где

2626\* MERGEFORMAT ()

потери напора во всасывающей трубе.

Местные потери напора во всасывающей трубе

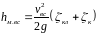
Потери напора по длине на всасывающей трубе

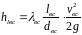
определяется по формуле Альтшуля 19.

Подставив в выражение 25 значения вакуума, скоростной высоты 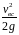и потери напора во всасывающей трубе, получим величину h_н.

Далее необходимо построить напорную линию, которая представляет собой график распределения напора по длине.

В пределах водоема напорная линия совпадает с линией поверхности воды, т.к. скоростью в пределах водоема пренебрегаем.

При входе в самотечную трубу напор скачкообразно уменьшается на величину потери напора на сетке самотечной трубы .

В плоскости входного сечения в самотечную трубу откладываем эту величину вниз от уровня воды в водоеме. Далее происходит потеря по длине, которая в конце участка самотечной трубы достигает величины

Для построения напорной линии с учетом потери напора по длине поступаем следующим образом. Из конца вертикального отрезка h_c проводим горизонтальную линию и в конце участка самотечной трубы откладываем от нее вниз величину h_l и соединяем наклонной линией концы отрезков h_c и h_l. В выходном сечении самотечного трубопровода происходит местная потеря на выходе, поэтому из конца наклонной линии откладываем величину .

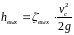Пьезометрическая линия P – P будет располагаться ниже напорной Н – H на величину скоростной высоты .

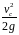Задача № 6

Расчет разветвленного тупикового газопровода при малом перепаде давления

Студентам предлагается рассчитать вентиляционный воздуховод, схема которого показана на рис.8. Вентилятор подает воздух в два помещения по каналам 3-4 и 3-5. На выходе из каналов установлены поворотные заслонки для регулировки расхода воздуха. Задачей гидравлического расчета является определение необходимого избыточного давления на входе в систему для подбора вентилятора при условии обеспечения заданных расходов воздуха на выходе из каналов 3-4 и 3-5.

Рис. 8

Основой расчетов газопроводов, так же как и для расчетов напорных трубопроводов для капельных жидкостей, является уравнение Бернулли. Но для газопроводов используется другая форма уравнения. Для расчета потоков капельных жидкостей в гидравлике принято оперировать понятием напора жидкости, который измеряется в метрах. По ряду причин напор не годится для оценки потоков газов. Например, потенциальный напор капельной жидкости определяется уровнем ее свободной поверхности, а газы не образуют свободной поверхности.

Уравнение Бернулли легко преобразуется таким образом, что все его члены измеряются не в метрах, а в паскалях, то есть представляют собой давления.

2727\* MERGEFORMAT ()

Уравнение (1) используется для расчета газопроводов. В нем ρ – плотность газа, g – ускорение свободного падения, z – геометрическая высота, p – давление газа, v – средняя скорость потока газа, - динамическое давление, Δp_w – потери давления, которые, так же как потери напора, отражают затраты энергии на преодоление сопротивлений движению жидкости.

Методика использования уравнения Бернулли определяется величиной перепада давления в газопроводе. Относительным перепадом давления называется отношение потери давления Δp к средней величине давления 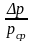(см. рис. 9).

газопровод

р₁

р₂

L

Рис. 9

Перепадом давления называется разность давлений в начале и в конце трубопровода а средняя величина давления вычисляется как их полусумма .

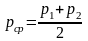Различают газопроводы с малыми переп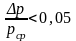адами давления и с большими перепадами давления .

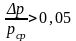Плотность газов, в отличие от плотности капельных жидкостей, сильно зависит от давления. Согласно уравнению Бернулли, при движении газа по трубопроводу происходят потери давления p, а, следовательно, изменяется плотность газа . Поэтому при гидравлическом расчете газопроводов возникает задача учета изменений плотности газа по длине потока. Но если плотность изменяется незначительно, ее изменениями можно пренебречь без существенного ущерба для точности расчета.

При расчете газопроводов с малым перепадом давления плотность газа считается постоянной величиной. При расчете газопроводов с большим перепадом давления необходимо учитывать изменения плотности газа по длине потока, что существенно усложняет гидравлический расчет. Вентиляционные трубопроводы относятся к газопроводам с малым перепадом давления.

В трубопроводах вентиляционных систем возникают значительные местные сопротивления, которые необходимо учитывать в гидравлических расчетах. Поэтому вентиляционные газопроводы рассчитываются как короткие трубопроводы.

Методика расчета в общих чертах заключается в следующем.

1. Задаются необходимые для вентиляции помещений расходы воздуха Q по соответствующим техническим нормативам.

2. Назначаются длины трубопроводов L в соответствии с размерами

вентилируемого объекта.

3. Выбирается материал трубопроводов и соответствующая величина

эквивалентной шероховатости Δ.

4. Задаются форма и размеры поперечного сечения трубопроводов, конструкция разветвлений, соединений труб разного диаметра,

отводов и регулирующих устройств.

5. На основе перечисленных исходных данных вычисляется потеря

давления в системе.

В воздушных вентиляционных системах величины гравитационного давления ρgz в уравнении 27 пренебрежимо малы по сравнению с другими членами уравнения. Поэтому для расчета используется упрощенное уравнение Бернулли в форме 28

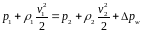2828\* MERGEFORMAT ()

Суммарная потеря давления Δp_w является суммой потерь по длине и местных потерь Δp_w = Δp_L + Δp_м . Потери по длине вычисляются по формуле

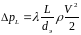2929\* MERGEFORMAT ()

где  - коэффициент гидравлического трения, L – длина рассматриваемого участка газопровода, d_э = 4R - эквивалентный диаметр живого сечения потока газа, R – гидравлический радиус живого сечения.

Местные потери вычисляются по формуле

3030\* MERGEFORMAT ()

в которой  -коэффициент местного сопротивления

Величины d_э для трубопроводов с различной формой поперечного сечения даны в таблице 6.

Таблица 6

dэ	Форма сечения
d d э = d
d a a э = a
b а

Рассмотрим расчет газопровода с малым перепадом давления на примере разветвленной тупиковой вентиляционной системы, изображенной на рисунке 8.

1. Заданы расходы воздуха в конце участков:

3-4 – 0,7 м³/с ,

5. – 0,4 м³/с .

2. Длины участков:

1-2 – 4м,

2-3 – 25м,

3-4 – 30 м,

5. – 10 м.

3. Поскольку трубопровод разветвленный, выбираем и рассчитываем

магистраль по признаку максимальной длины трубопровода 1-2-3-4.

Участок 3-5 будем рассматривать как ответвление магистрали. Расчет удобно вести в табличной форме. Для этого создаем таблицу 7.

4. Трубопроводы из шлакогипсовых плит с шероховатостью поверхности мм.

5. Трубопроводы прямоугольного поперечного сечения с размерами, указанными в таблице 7.

6. Максимальная допускаемая скорость потока воздуха из условия допускаемого уровня шума V_доп = 12 м/с.

7. Коэффициенты местных сопротивлений:

отводы (колена) на участках 2-3 и 3-4 _k = 1,2,

поворотные заслонки на выходе участков 3-4 и 3-5, полностью открытые _з = 1,6 ,

прямой проход через тройник на магистрали _тп = 0,13,

отвод через тройник в ответвление _то = 2,7.

8. Расходы на участках 1-2 и 2-3 равны сумме расходов на участках 3-4 и 3-5:

Q_1-2 = Q_2-3 = 0,7 + 0,4 = 1,1 м³/с.

9. Вычисляем скорости на участках по формуле V = Q/ Если вычисленные скорости больше допускаемой, сечения трубопроводов надо увеличить.

10. Вычисляем динамическое давление по формуле .

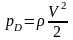При малом перепаде давления плотность можно считать постоянной.

Принимаем ее равной плотности воздуха в стандартных условиях (20⁰С; 101,325 кПа) = 1,2 кг/м³.

11. Вычисляем коэффициент гидравлического трения по формуле Альтшуля

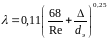3131\* MERGEFORMAT ()

Число Рейнольдса вычисляем по формуле

3232\* MERGEFORMAT ()

Эквивалентный диаметр d_э определяем, пользуясь таблицей 6.

Кинематический коэффициент вязкости воздуха в стандартных условиях можно принимать равным ν = 15,06 ^. 10^-6 м²/с.

12. Вычисляем потери давления по длине по формуле 29.

13. Записываем в таблицу величины коэффициентов местного сопротивления и вычисляем суммарные коэффициенты сопротивления участков.

14. Вычисляем местные потери давления на участках по формуле30, суммарные потери на участках 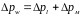и суммарную потерю давления в магистрали.

На основе величины суммарной потери давления в магистрали заключаем, что для обеспечения заданных расходов воздуха необходим вентилятор, создающий давление на входе в газопровод около 300 Па.

Выполненные расчеты показали, что в ответвлении 3-5 при заданном расходе Q_3-5 = 0,4 м³/с потеря давления составит 82,86 Па. На участке 3-4 магистрали расчетная потеря давления 113,03 Па. Это означает, что гидравлическое сопротивление в ответвлении меньше, чем в магистрали. При этом расход в ответвлении будет больше, а в магистрали меньше заданных величин. Для обеспечения заданных расходов необходимо уравнять потери давления в ответвлении и в магистрали. Для этого можно увеличить потери давления в ответвлении, частично закрывая поворотную заслонку на выходе участка 3-5. Определим необходимый угол открытия заслонки α°.

Потерю давления в ответвлении надо увеличить на p = 113,03 – 82,86 = 30,17 Па (см. таблицу 7). Для этого надо увеличить коэффициент местного сопротивления поворотной заслонки на выходе участка 3-5 на величину _з , которую можно вычислить по формуле (4)

Суммарный коэффициент местного сопротивления заслонки должен быть равным

_з + _з = 1,6 + 1,93 = 3,53

Необходимый для этого угол открытия заслонки ^^находим, пользуясь таблицей 8.

Таблица 7

Параметр	Обозначение	Ед. изм.	Магистраль					Ответвление
			3-4	2-3	1-2		3-5
Заданный расход в конце участка	Qз	м3/с	0,7	-	-		0,4
Длина участка	L	м	30	25	4		10
Эквивалентная шероховатость	Δ	мм	1
Размеры сечений	a . b	мм	280 . 420			280 . 280
Допускаемая скорость	Vдоп	м/с	12
Расход на участках	Q	м3/с	0,7	1,1	1,1	0,4
Скорость на участках	V	м/с	5,95	9,35	9,35	5,1
Динамическое давление	pD	Па	21,24	52,45	52,45	15,6
Эквивалентный диаметр	dэ	мм	336			280
Число Рейнольдса	Re	-	132700	208600		94800
Коэффициент гидравлического трения	λ	-	0,027	0,026		0,028
Потери давления по длине	ΔpL	Па	50,74	102,99	16,48	15,70
Коэффициенты местных сопротивлений	ζтп	-	0,13	-	-	-
	ζк	-	1,2	1,2	-	-
	ζтo	-	-	-	-	2,7
	ζз	-	1,6	-	-	1,6
	Σζ	-	2,93	1,2	-	4,3
Местные потери давления	ΔpM	Па	62,29	63,00	0	67,16
Суммарные потери на участках	ΔpW	Па	113,03	165,99	16,48	82,86
Суммарная потеря в магистрали	ΔpW	Па	295,50

Таблица 8

	90	85	80	75	70	65	60	55	50	45	40	35	30	25	20	15
	1,6	1,8	2,0	2,3	2,6	2,9	3,3	3,8	4,4	5,2	6,1	7,4	9,2	12,3	18	31

Таблица 9

Варианты заданий

№	Материал	, мм	Сечения, м			Расходы, м3/с			Длины, м
			1-2-3-4	3-5	3-4		3-5	1-2		2-3	3-4	3-5
1	Лист. сталь	0,1	0,2*	0,1	0,25		0,08	4		18	28	22
2			0,25*	0,15	0,4		0,15	4		18	28	22
3	Фанера	0,2	0,2 . 0,15	0,15 . 0,15	0,2		0,15	4		17	27	21
4			0,25 . 0,2	0,2 . 0,15	0,4		0,15	4		16	25	20
5	Шлакогипс	1,0	0,28 . 0,28	0,28 . 0,14	0,6		0,3	4		15	23	19
6			0,42 . 0,28	0,28 . 0,28	1,0		0,4	4		15	23	19
7	Шлакобетон	1,5	0,2 . 0,15	0,15 . 0,1	0,23		0,12	4		14	22	18
8			0,2 . 0,2	0,15 . 0,15	0,3		0,15	4		13	21	17
9	Кирпичная кладка	5	0,27 . 0,14	0,14 . 0,14	0,25		0,15	4		12	19	15
10			0,4 . 0,27	0,27 . 0,14	0,8		0,4	4		12	19	15
№	Материал	, мм	Сечения, м			Расходы, м3/с			Длины, м
			1-2-3-5	3-4	3-4		3-5	1-2		2-3	3-4	3-5
11	Листовая сталь	0,1	0,2*	0,1*	0,08		0,25	4		10	27	36
12			0,25*	0,15*	0,15		0,40	4		10	26	34
13			0,3*	0,2*	0,20		0,60	4		10	25	32
14	Фанера	0,2	0,20∙0,15	0,15∙0,15	0,15		0,20	4		10	24	30
15			0,25∙0,20	0,20∙0,15	0,15		0,40	4		10	23	28
16			0,30∙0,25	0,20∙0,15	0,30		0,60	4		10	22	26
17	Шлакогипс	1,0	0,28∙0,28	0,28∙0,14	0,30		0,60	4		10	21	24
18			0,42∙0,28	0,28∙0,28	0,40		1,00	4		10	20	23
19			0,42∙0,42	0,42∙0,28	0,75		1,25	4		10	19	22
20	Шлакобетон	1,5	0,20∙0,15	0,15∙0,10	0,12		0,23	4		10	18	21
21			0,20∙0,20	0,15∙0,15	0,15		0,30	4		10	17	20
22			0,30∙0,20	0,20∙0,15	0,25		0,45	4		10	16	19
23	Кирпичная кладка		0,27∙0,14	0,14∙0,14	0,15		0,25	4		10	15	18
24			0,40∙0,27	0,27∙0,14	0,40		0,80	4		10	14	17
25			0,40∙0,40	0,40∙0,27	0,90		1,00	4		10	13	16

*) Диаметр трубопровода круглого поперечного сечения, в других вариантах трубопроводы прямоугольного сечения а·в, или квадратного а∙а.
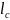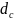
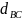