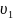Задача № 4

У тепловоза в течение времени t равномерно изменяется скорость от 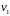до , в результате чего изменяется форма свободной поверхности жидкости в прицепленной к нему цистерне. Цистерна заполнена наполовину жидкостью плотностью . Диаметр цистерны D, длина L.

Требуется:

1. Получить уравнение свободной поверхности жидкости в цистерне.

2. Насколько повысится или понизится уровень жидкости у передней стенки (по ходу движения цистерны).

3. Определить величину избыточного гидростатического давления в точке, указанной в каждом варианте задания (см. рис. 6) на поверхности жидкости в резервуаре давление равно атмосферному p_а.

Рис. 6

Таблица 4

№ вар.			t		L	D	Название точки
-	км/ч	км/ч	с	кг/м3	м	м	-
1	5	20	7	1000	8,7	2,3	А
2	20	5	6	890	14,7	3,0	В
3	40	30	4	650	9,4	2,0	А
4	45	30	5	900	10	2,8	В
5	50	30	5	850	14,7	3,0	А
6	70	36	10	830	9,6	2,6	В
7	20	10	5,5	800	6,7	2,2	А
8	10	30	6	1000	14,0	3,0	В
9	5	25	10	1100	6,8	2,0	А
10	10	40	5	790	12	2,5	В
11	4	18	6	1000	8,7	2,1	А
12	18	4	5	890	14,7	3,1	В
13	36	26	4	950	9,4	2,2	А
14	42	27	5	900	10	2,7	В
15	48	28	5	850	14,7	2,9	А
16	22	10	6	830	9,6	2,5	В
17	8	28	6	800	6,7	2,0	А
18	7	27	10	1000	14,0	2,6	В
19	12	42	5	1100	6,8	2,5	А
20	42	32	4	790	12,0	2,7	В
21	46	32	5	1000	9,4	3,2	А
22	52	32	5	890	10,0	3,0	В
23	68	34	10	950	14,7	3,1	А
24	22	12	5,5	900	9,6	2,6	В
25	12	32	6,0	850	6,7	2,8	А

Указанию к решению задачи 4.

1. Для получения уравнения свободной поверхности жидкости нужно воспользоваться общим, объединенным уравнением равновесия жидкости, выраженным в дифференциальной форме:

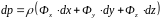1111\* MERGEFORMAT ()

и применить его к жидкости, находящейся под действием сил тяжести и сил инерции.

В этом случае в формуле 11 гидростатическое давление на свободной поверхности жидкости равно p_а = const; , 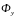и  – проекции на соответствующие оси координат объемных сил, действующих на единицу массы жидкости. При этом Ф_x = - a; Ф_y = 0; Ф_z = - g. Горизонтальное ускорение a, м/с², определяется по формуле 12

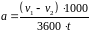1212\* MERGEFORMAT ()

После этого решается полученное дифференциальное уравнение и находится уравнение свободной поверхности.

2. Для получения ответа на второй вопрос нужно в полученное уравнение свободной поверхности подставить координаты указанной в каждом варианте точки.

3. Для определения величины избыточного гидростатического давления в заданной точке снова обращаемся к дифференциальному уравнению 11 и решаем его относительно p

1313\* MERGEFORMAT ()

где Ф_x = - a; Ф_y = 0; Ф_z = - g.

Величину "С" определяем, записав уравнение 13 для начала координат. Подставляя в полученное окончательное выражение для p координаты указанной в задании точки, получим величину избыточного гидростатического давления в ней.