Тема 3. Реальные газы

1.10. Отклонение газов от идеальности.

Как уже отмечалось, поведение реальных газов довольно хорошо описывается уравнением (5)

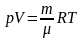
только при не слишком высоких давлениях и достаточно высоких температурах. С повышением давления и уменьшением температуры наблюдаются значительные отступления от уравнения. Во втором столбце таблицы 1 приведены значения произведения pV для массы азота, занимающей при нормальных условиях объем, равный одному литру. Указанные значения даны для различных давлений и одной и той же температуры 0°С. В соответствии с уравнением (5) произведение pV при неизменной температуре должно оставаться постоянным. В действительности, как видно из таблицы, при давлениях порядка 200 ат наблюдаются заметные отклонения, которые, непрерывно возрастая с увеличением давления, достигают при 1000 ат более 100%. Эти отклонения не представляются удивительными, поскольку в модели идеального газа не учитываются размеры молекул и их взаимодействие друг с другом на расстоянии. Вместе с тем при повышении давления возрастает плотность газа, что приводит к уменьшению среднего расстояния между молекулами; поэтому объем молекул и взаимодействие между ними начинают играть существенную роль.

1.11. Потенциальная энергия взаимодействия молекул

Характер взаимодействия между молекулами лучше всего показать с помощью приведенной на рис. 6 кривой, изображающей взаимную потенциальную энергию двух молекул как функцию расстояния r между их центрами. При построении этой кривой потенциальная энергия молекул, находящихся на бесконечно большом расcтоянии друг от друга (т. е. когда они не взаимодействуют), положена равной нулю. Следовательно, кривая идет так, что при r, стремящемся к бесконечности, асимптотически приближается к оси r.

Рис.6. Зависимость потенциальной энергии взаимодействия молекул от расстояния между молекулами

Зная потенциальную энергию как функцию r, можно определить силу, с которой взаимодействуют молекулы на разных расстояниях друг от друга. Для этого нужно воспользоваться известным из механики соотношением

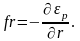
Знак «–» здесь отражает то обстоятельство, что силы, с которыми взаимодействуют молекулы, стремятся перевести их в состояние с наименьшей потенциальной энергией. Следовательно, на расстояниях, превышающих r₀, между молекулами действуют силы взаимного притяжения, а на расстояниях, меньших r₀, – силы отталкивания. Крутизна хода кривой в соответствующем месте дает величину силы.

Рассмотрим с помощью кривой ε_Р процесс сближения (соударения) молекул. Поместим мысленно центр одной из молекул в начало координат, а центр второй молекулы представим перемещающимся по оси r. Пусть вторая молекула летит по направлению к первой из бесконечности, имея начальный запас кинетической энергии ε_k = ε₁. Приближаясь к первой молекуле, вторая под действием силы притяжения движется со все возрастающей скоростью. В результате кинетическая энергия молекулы ей также растет. Однако полная энергия системы, равная ε = ε_k + ε_р, остается неизменной (система двух молекул замкнута) и равной ε₁ так как одновременно уменьшается потенциальная энергия ε_р. При прохождении молекулой точки с координатой r₀ силы притяжения сменяются силами отталкивания, вследствие чего молекула начинает быстро терять скорость (в области отталкивания кривая ε_р идет очень круто). В момент, когда потенциальная энергия ε_р становится равной полной энергии системы ε₁, скорость молекулы обращается в нуль. В этот момент имеет место наибольшее сближение молекул друг с другом. Минимальное расстояние d₁, на которое могут сблизиться центры молекул, представляет собой эффективный диаметр молекулы. После остановки молекулы все явления протекают в обратной последовательности: сначала молекула движется со все возрастающей скоростью под действием силы отталкивания; миновав расстояние r₀, молекула попадает под действие замедляющей ее движение силы притяжения и, наконец, удаляется на бесконечность, имея первоначальный запас кинетической энергии ε₁.

Из рис. 6 видно, что в случае, когда молекула начинает свое движение из бесконечности с большим запасом энергии ε₂, минимальное расстояние d₂, на которое сближаются центры молекул, оказывается меньшим. Таким образом, эффективный диаметр молекул зависит от их средней энергии, а следовательно, и от температуры. С повышением температуры эффективный диаметр молекул d уменьшается, вследствие чего средняя длина свободного пробега λ растет.

Рис.7. Зависимость потенциальной энергии взаимодействия молекул от расстояния между молекулами в модели идеального газа

Характер взаимодействия между молекулами, предполагавшийся при выводе уравнения состояния идеального газа, соответствует потенциальной кривой, изобра­женной на рис. 7. На расстояниях, превышающих r₀, ε_р постоянна, вследствие чего сила равна нулю. При r = r₀ ε_р обращается в бесконечность, образуя потен­циальный барьер, препятствующий сближению центров молекул на расстояния, меньшие r₀. Такое упрощенное рассмотрение допустимо, если средние расстояния между молекулами в газе достаточно велики: при больших r кривая ε_р на рис. 6 идет очень полого, вследствие чего 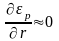. По мере же уменьшения среднего расстояния между молекулами, т. е. при увеличении плотности газа, роль сил притяжения между молекулами все больше растет. Одновременно, как мы видели выше, сокращается та часть занимаемого газом объема, в пределах которой может происходить движение молекул.