2.5.Работа, совершаемая газом при расширении
Вычислим работу, совершаемую газом при расширении или сжатии, т. е. при изменении объема. Представим себе, что газ находится в цилиндре, который закрыт подвижным поршнем, имеющим площадь S (рис. 32). Пусть под действием приложенной внешней силы F поршень опустился на расстояние dx, сжав при этом газ. Газ будет сжиматься до тех пор, пока сила F не уравновесится силой, действующей на поршень со стороны газа и равной pS, где р — давление газа. Работа dA, затраченная на перемещение поршня на расстояние dx, равна, очевидно, pSdx. Но Sdx есть не что иное, как изменение объема газа dV при сжатии, т. е.
Sdx = — dV,
откуда
dA = — pdV. (78)
Наоборот, при расширении газа, т. е. при увеличении объема на dV, газ сам совершает работу против внешних сил, равную + рdV.
Изменение объема газа сопровождается работой, равной произведению давления, под которым находится газ, на изменение его объема.
Рис. 32. К вычислению работы при изменении объема газа
Формула (78) верна не только для газа, но и для любых тел. Если при изменении состояния тела внешняя работа совершается только за счет изменения объема, то первое начало термодинамики можно написать в виде:
dQ = dU + pdV. (79)
Возможны случаи, когда изменение состояния тел сопровождается изменением электрических, магнитных или других параметров, тогда к правой части уравнения следует добавить соответствующие слагаемые: электрическую, магнитную и другие виды энергии. Мы ограничимся здесь рассмотрением изменения только параметров р и V.
Можно вычислить внешнюю работу и в том случае, когда изменение параметров состояния не бесконечно мало.
Если тело переходит из состояния 1 в состояние 2, то связанная с этим работа А определяется путем интегрирования уравнения (78):
.
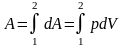Этот интеграл можно определить графически. Действительно, состояние тела, как было указано, характеризуется точкой на кривой р — f(V). Поэтому, если зависимость р — f(V) построена графически, например, если эта зависимость выражается кривой I на рис. 33, то интеграл
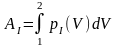
равен заштрихованной площади под этой кривой.
Рис. 33. Графическое изображение работы при изменении состояния системы
Если переход из состояния 1 в состояние 2 происходит так, что изменение давления с объемом изображается кривой II, то связанная с этим переходом работа будет другой:
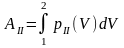
Для переходов, соответствующих кривым I и II, функции pI(V) и pII(V) будут разными, следовательно, работы AI и AII будут разными.
Внешняя работа, произведенная телом (или над ним) при изменении его объема, зависит от последовательности состояний, которую проходит тело от начального в конечное состояние.
Что касается внутренней энергии U, то она зависит только от состояния тела и ее изменение не зависит от промежуточных состояний, в которых тело пребывало.
Термодинамическое состояние системы характеризуется определенной внутренней энергией системы. Однако ни работы, ни теплоты в системе нет. Работа производится системой или над системой, соответственно теплота передается системе или отбирается у системы. Поэтому для приращения внутренней энергии можно записать ΔU = U2 – U1 (здесь U2 и U1 значения внутренней энергии системы в состояниях 1 и 2). Для теплоты и работы таких выражений написать невозможно, поскольку в каждом конкретном состоянии в системе нет ни теплоты, ни работы. Поэтому величины Q и A в формуле (77) не обозначают приращение теплоты и работы.
С математической точки зрения изменение внутренней энергии является полным дифференциалом. Изменение внутренней энергии можно выразить через изменения параметров системы (здесь мы имеем в виду не только идеальный газ):
Для теплоты и работы такого выражения написать нельзя, поскольку теплота и работа не являются полными дифференциалами. Для обозначения бесконечно малых изменений таких величин вместо латинской буквы d применяется греческая буква δ, и первое начало термодинамике записывается в следующем виде:
δQ = dU + δA. (80)