2.6.Прямолинейное движение.

Найдем кинематические уравнения точки, движущейся по прямой. Направим ось OX вдоль траектории движения (рис. 7). Рассмотрим сначала равномерное движение v = const. Тогда элементарное перемещение (перемещение за бесконечно малый промежуток времени) будет равно dx = vdx. Пусть в момент времени t = 0 точка имела координату x₀. Тогда изменение координаты за время t равно:

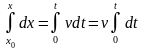
x – x₀ = vt,

x = x₀ + vt. (8)

Знаки «плюс» перед x₀ и v говорят о том, что при выбранных направлениях оси OX и начальном положении точки координата x₀ и проекция скорости на ось OX положительны.

Рис. 7.

Прямолинейное движение

Если скорость изменяется во времени, то такое движение называется движением с ускорением, или движением с переменной скоростью. Если ускорение постоянно, то такое движение называется равнопеременным:

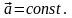(9)

При этом если вектора скорости и ускорения 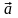параллельны (как на рис. 7), то такое движение называется равноускоренным: за одинаковые промежутки времени скорость тела увеличивается на одну и ту же величину.

Если вектора скорости и ускорения антипараллельны (на рис. 7 эти вектора должны быть направлены в противоположные стороны), то такое движение называется равнозамедленным: за одинаковые промежутки времени скорость тела уменьшается на одну и ту же величину.

Использование определения (9) позволяет вывести зависимости скорости v от времени t при равнопеременном движении. Так, выбрав ось координат вдоль направления движения тела (рис. 7), можно записать: dv = adt. Если тело в момент времени t = 0 тело имело скорость v₀, то

,

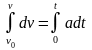v – v₀ = at.

Таким образом, при равнопеременном движении тела по прямой его скорость меняется по закону:

v = v₀ ± at. (10)

Знак «плюс» в этой формуле соответствует равноускоренному движению, знак «минус» – равнозамедленному.

Теперь выведем зависимость координаты х тела от времени t при равноускоренном движении.

Выбрав ось координат ОХ вдоль направления движения тела, можно вновь записать:

dx = vdt = (v₀ ± at)dt.

Полагая, что моменту времени t = 0 соответствует координата x₀, получаем:

;

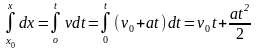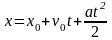. (11)

Какой знак («плюс» или «минус») следует поставить перед начальной скоростью v₀ и ускорением a, зависит от того, совпадают ли (знак «плюс») или нет (знак «минус») направления соответственно векторов 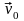и с направлением выбранной оси координат ОХ.

Рис. 8.

Графики, описывающие движение точки по прямой

На рис. 8 приведены примеры графиков зависимостей от времени координаты, скорости и ускорения при равномерном, равноускоренном и равнозамедленном движении.

Часто любое равнопеременное движение называют просто ускоренным, имея в виду, что если скорость возрастает, то ускорение является положительной величиной, а если скорость уменьшается, то ускорение является отрицательной величиной.