2.3. Декартова прямоугольная система координат

Для определения положения точки в пространстве мы будем использовать декартовы прямоугольные координаты (рис.2).

Декартова прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY, OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. Ось OX называется осью абсцисс (или просто абсциссой), ось OY – осью ординат (ординатой), ось OZ – осью аппликат (аппликатой).

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки параллельно плоскостям YOZ, XOZ и XOY соответственно.

Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Символически это записывают так:

A(x, y, z),

или

A = (x, y, z),

или привязывают запись координат к конкретной точке с помощью индекса:

x_A, y_A, z_A,

и т. п.

Рис. 2.

Декартова прямоугольная система координат

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче, приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B лежала не как на рисунке — на луче OX, а на его продолжении в обратную сторону от точки O (на отрицательной части оси OX), то абсцисса x точки A была бы отрицательной (минус расстоянию OB). Аналогично и для двух других осей.

Координатные оси OX, OY, OZ, изображенные на рис. 2, образуют правую систему координат. Это означает, что если смотреть на плоскость YOZ вдоль положительного направления оси OX, то движение оси OY в сторону оси OZ будет проходить по часовой стрелке. Эту ситуацию можно описать при помощи правила буравчика: если буравчик (винт с правой резьбой) вращать по направлению от оси OY к оси OZ, то он будет двигаться вдоль положительного направления оси OX.

Векторы единичной длины, направленные вдоль координатных осей, называются координатными ортами. Их обозначают обычно как 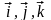(рис. 3). Встречается так же обозначение Орты составляют базис координатной системы. В случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

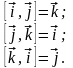
Положение точки в пространстве можно описать с помощью радиус-вектора

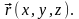
Радиус-вектор – это вектор, проведенный из начала координат в точку, где находится тело (рис. 3.). Радиус-вектор можно разложить на составляющие:

где — единичные векторы (орты), x, y, z – координаты точки.

Рис. 3.

Базис декартовой прямоугольной системы координат

2.4. Перемещение. Пройденный путь

При перемещении в пространстве точка A занимает ряд последовательных положений. Линия, описываемая в пространстве движущейся точкой, называется траекторией. В зависимости от вида траектории движение делят на прямолинейное и криволинейное. Частным случаем криволинейного движения является движение по окружности.

Траектория – линия, описываемая в пространстве движущейся точкой.

Пусть материальная точка, двигаясь по некоторой траектории, переместилась из точки 1 в точку 2 (рис. 4). Длина траектории точки S₁₂ между положениями 1 и 2 называется пройденным путем. Если материальная точка повернет обратно и дойдет до точки 3, то полный путь равен S = S₁₂ + S₂₃. Пройденный путь всегда выражается положительным числом.

Пройденный путь – длина траектории между начальным и конечным положениями точки.

Вектор, соединяющий начальное и конечное положение точки, называется перемещением (рис. 5). Обычно перемещение обозначают 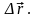Вектор перемещения – это разница между радиус-векторами начального и конечного положения точек: 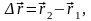или 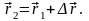При прямолинейном движении перемещение совпадает с соответствующим участком траектории. Если материальная точка участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме ее перемещений, совершаемых ею за тоже время в каждом из движений порознь.

Перемещение – величина векторная, пройденный путь – величина скалярная.

Пройденный путь и перемещение в системе СИ измеряются в метрах.

Движение точки считаются полностью определенным, если заданы уравнения, описывающие изменение координат точки со временем:

x = x(t); y = y(t); z = z(t). (1)

Эти уравнения являются математическим выражением закона движения точки. Если положение точки в пространстве задается радиус-вектором, то закон движения точки можно записать в векторном виде:

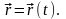(2)

Уравнения (1) и (2) называются кинематическими уравнениями движения точки.

Рис. 4.

Траектория и пройденный путь

Рис. 5.

Вектор перемещения точки