4.8. Кинетическая энергия вращения

Определим теперь работу, совершаемую моментом сил при поворачивании тела на определенный угол φ вокруг неподвижной оси 00' (рис. 34). Пусть к твердому телу приложена сила F, касательная к траектории точки приложения, момент которой относительно оси 00' равен М = Fr. При поворачивании тела на угол Δφ точка приложения силы А переместится на длину дуги Δs, откуда работа, совершенная силой F, будет:

ΔA = F*Δs.

Длина дуги равна

Δs = r*Δφ,

где Δφ – угол поворота тела, следовательно,

ΔA = F*r*Δφ,

или, так как F*r = M есть момент силы F,

ΔA = M*Δφ. (92)

Таким образом, работа, совершаемая при поворачивании тела на угол Δφ, численно равна произведению из момента силы на угол поворота.

Рис. 34.

Работа силы, вызывающей вращение

При переменном моменте силы М выражение (92) записывается в дифференциальном виде

dA = M(φ)dφ,

и для вычисления полной работы при повороте на некоторый угол производится интегрирование.

В случае, если момент М постоянен, работа, совершаемая при поворачивании тела на конечный угол φ, будет равна:

A = M*φ. (93)

Рассмотрим теперь тело, вращающееся с данной угловой скоростью ω вокруг неподвижной оси. Кинетическая энергия его i-гo элемента будет:

,

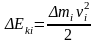где Δm_i — масса этого элемента и v_i — его линейная скорость. Так как v_i = r_iω, то

.

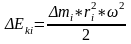Кинетическая энергия вращения всего тела равна сумме кинетических энергий его отдельных элементов:

.

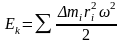Поскольку все точки абсолютно твердого тела вращаются с одинаковой скоростью, можно записать:

.

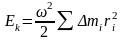Но по формуле (76) 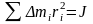есть момент инерции тела (относительно оси вращения), откуда

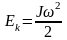. (94)

Таким образом, кинетическая энергия вращения твердого тела вокруг неподвижной оси выражается формулой, совершенно аналогичной формуле, дающей кинетическую энергию материальной точки, только роль массы т играет момент инерции J, а роль линейной скорости — угловая скорость ω.

5. Механические свойства жидкостей и твердых тел

5.1. Давление в жидкости и газе.

Разделы механики, занимающиеся изучением жидкостей и газов, называются гидромеханикой и аэромеханикой. Они в свою очередь подразделяются на гидро- и аэростатику (изучающие равновесие жидкостей и газов) и гидро- и аэродинамику (изучающие движение жидкостей и газов). В настоящей главе излагается статика.

Жидкие и газообразные тела характерны тем, что не оказывают сопротивления сдвигу и поэтому способны изменять свою форму под воздействием сколь угодно малых сил. Для изменения объема жидкости или газа требуются, напротив, конечные внешние силы. При изменениях объема, происходящих в результате внешних воздействий, в жидкости и газе возникают упругие силы, в конце концов, уравновешивающие действие внешних сил. Упругие свойства жидкостей и газов проявляются в том, что отдельные части их действуют друг на друга или на соприкасающиеся с ними тела с силой, зависящей от степени сжатия жидкости или газа. Это воздействие характеризуют величиной, называемой давлением. Давление – это сила, действующая на единичную площадку:

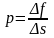(95)

Давление в газе определяется аналогичным образом.

Давление — скаляр, так как величина его в данной точке жидкости (или газа) не зависит от ориентации площадки Δs, к которой отнесено давление.

На первый взгляд может показаться удивительным, что пропорциональное векторной величине (силе) давление оказывается скалярной величиной. Однако следует иметь в виду, что площадка Δs также может рассматриваться как вектор, имеющий направление нормали к Δs, т. е. такое же направление, как и вектор силы, действующей на площадку. Следовательно, давление, по существу, равно отношению двух коллинеарных векторов Δf и Δs, а такая величина, как известно, представляет собой скаляр.

Единицами давления являются:

1. в СИ — н/м²;

2. в системе СГС – дин/см².

Кроме того, для измерения давления часто пользуются следующими внесистемными единицами:

1) технической атмосферой (обозначается ат), равной 1 кгс/см²;

2) физической или нормальной атмосферой (обозначается атм), равной давлению, оказываемому столбом ртути высотой 760 мм.

В физике часто измеряют давление в миллиметрах ртутного столба. Между различными единицами давления имеются следующие соотношения:

1 мм рт. ст. = 0,001 м * 13,6 * 10³кг/м³ * 9,81 м/сек²= 133н/м² = 133Па;

1 атм = 760 * 133= 1,01 • 10⁵ н/м² = 1,033 ат;

1 ат = 9,81 • 10⁴ = 0,981 • 10⁵ н/м² = 0,968 атм.

Рис. 35.

Давление в жидкости

Если бы в жидкости (или газе) не было объемных сил, то условием равновесия было бы постоянство давления во всем объеме (закон Паскаля). Действительно, выделим в жидкости небольшой произвольно ориентированный цилиндрический объем высотой Δl и с основанием ΔS (рис. 35а). Если бы в точках, отстоящих друг от друга на Δl, давление отличалось на Δр, то вдоль оси цилиндра действовала бы сила Δp*ΔS, вследствие чего жидкость пришла бы в движение и равновесие было бы нарушено. Следовательно, при отсутствии объемных сил в состоянии равновесия в любом месте жидкости должно выполняться условие , откуда следует, что р = const.