3.14.Законы движения планет Кеплера
Основанием для установления закона всемирного тяготения Ньютону послужили три открытых Кеплером закона движения планет:
1. Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
2. Радиус-вектор планеты описывает за равные времена одинаковые площади.
3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.
Первый закон Кеплера указывает на то, что планеты движутся в поле центральных сил. Траектория тела в поле центральных сил представляет собой плоскую кривую — гиперболу, параболу или эллипс, — фокус которой совпадает с центром сил.
Принимая для простоты, что орбиты являются не эллипсами, а окружностями (это допустимо, так как практически орбиты всех планет мало отличаются от окружностей), ускорение, с которым движется планета, можно написать в виде
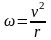
где v — скорость движения планеты, r — радиус орбиты. Заменим v через 2πr/T (T — период обращения планеты вокруг Солнца):
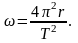
На основании последнего выражения отношение сил, действующих на планеты со стороны Солнца, запишется следующим образом:
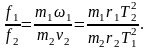
Заменяя в соответствии с третьим законом Кеплера отношение квадратов периодов обращения отношением кубов радиусов орбит, получим:
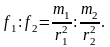
Таким образом, из третьего закона Кеплера следует, что сила, с которой планета притягивается к Солнцу, пропорциональна массе планеты и обратно пропорциональна квадрату ее расстояния до Солнца.
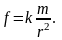
Предположив, что коэффициент пропорциональности k в свою очередь пропорционален массе Солнца Мс, Ньютон пришел к уже знакомой нам формуле
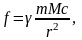
выражающей закон всемирного тяготения.
Второй закон Кеплера является следствием закона сохранения момента импульса. Из рис. 21 видно, что описанная радиусом-вектором за время dt площадь dS равна половине произведения основания треугольника vdt на высоту треугольника l, которая совпадает с плечом импульса планеты тv по отношению к Солнцу:
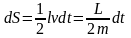
(L — момент импульса планеты, равный mvl).
Выражение
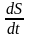называется
секториальной скоростью.
Таким образом,
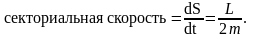
Момент импульса в центральном поле сил остается постоянным, следовательно, и секториальная скорость планеты должна быть постоянной. Это означает, что за равные промежутки времени радиус-вектор будет описывать одинаковые площади.
Рис. 21.
Секториальная скорость движения планеты
3.15. Механическая работа
Пусть тело, на которое действует сила , проходит, двигаясь по некоторой траектории, путь s. При этом сила либо изменяет скорость тела, сообщая ему ускорение, либо компенсирует действие другой силы (или сил), противодействующей движению. Действие на пути s характеризуется величиной, которая называется работой.
Механической работой называется скалярная величина, равная произведению проекции силы на направление перемещения Fs и пути s, проходимого точкой приложения силы (рис. 22):
A = Fs*s. (56)
Выражение (56) справедливо в том случае, если величина проекции силы Fs на направление перемещения (т. е. на направление скорости) остается все время неизменной. В частности, это имеет место, когда тело движется прямолинейно и постоянная по величине сила образует с направлением движения постоянный угол α. Поскольку Fs = F * cos(α), выражению (47) можно придать следующий вид:
A = F * s * cos(α).
Если
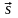– вектор перемещения, то работа
вычисляется как скалярное произведение
двух векторов
и
:
.
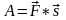(57)
Работа — алгебраическая величина. Если сила и направление перемещения образуют острый угол (cos(α) > 0), работа положительна. Если угол α — тупой (cos(α) < 0), работа отрицательна. При α = π/2 работа равна нулю. Последнее обстоятельство особенно отчетливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе. В обыденном понимании всякое усилие, в частности и мускульное напряжение, всегда сопровождается совершением работы. Например, для того чтобы держать тяжелый груз, стоя неподвижно, а тем более для того, чтобы перенести этот груз по горизонтальному пути, носильщик затрачивает много усилий, т. е. «совершает работу». Однако это – «физиологическая» работа. Механическая работа в этих случаях равна нулю.
Рис. 22.
Работа при перемещении под действием силы
Если величина проекции силы на направление перемещения не остается постоянной во время движения, то работа выражается в виде интеграла:
.
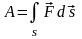(58)
Интеграл такого вида в
математике называются криволинейным
интегралом вдоль траектории S. Аргументом
здесь служит векторная переменная
,
которая может меняться как по модулю,
так и по направлению. Под знаком интеграла
стоит скалярное произведение вектора
силы
и вектора элементарного перемещения
.
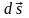За единицу работы принимается работа, совершаемая силой, равной единице и действующей в направлении перемещения, на пути, равном единице. В СИ единицей работы является джоуль (Дж), который равен работе, совершаемой силой в 1 ньютон на пути в 1 метр:
1Дж = 1Н * 1м.
В СГС единицей работы является эрг, равный работе, совершаемой силой в 1 дину на пути в 1 сантиметр. 1Дж = 107эрг.
Иногда применяется внесистемная единица килограммометр (кГ*м). Это работа, совершаемая силой в 1 кГ на пути в 1 метр. 1кГ*м = 9,81 Дж.