3.4. Третий закон Ньютона

Из первого и второго закона Ньютона следует, что причиной изменения скорости тела является действующая на это тело сила. С другой стороны, сила – это результат взаимодействия тел. Опыт показывает, что взаимодействие двух тел всегда вызывает появление двух сил: одна сила – результат действия первого тела на второе (обозн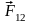ачим эту силу ), другая сила – результат действия второго тела на первое (обозначим эту силу 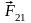). Эти силы равны по величине и направлены в разные стороны, т. е. подчиняются следующему векторному равенству:

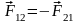(34)

Формула (34) является математическим выражением третьего закона Ньютона:

силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению.

Третий закон Ньютона является обобщением опытных фактов. Опыт показывает, что действия тел друг на друга носит характер взаимодействия: одно тело влияет на другое точно так же, как и второе на первое. Силы взаимодействия и , которые возникают при этом, обладают следующими особенностями:

• эти силы равны по величине и противоположно направлены;

• силы взаимодействия возникают всегда парами;

• они имеют одну физическую природу;

• силы взаимодействия приложены к разным телам.

Одну из сил часто называют «действием», а другую – «противодействием». В формулировке самого Ньютона третий закон механики гласит: «действию всегда есть равное и противоположное противодействие, иначе — действия двух тел друг на друга между собою равны и направлены в противоположные стороны». В такой формулировке «действию» неявно отводится главенствующая, а «противодействию» — подчиненная роль. На самом деле обе силы равноправны.

Таким образом, каждой силе, приложенной к какому-либо телу, соответствует равная по величине и противоположно направленная сила той же природы, приложенная к другому телу.

При поверхностном взгляде на третий закон Ньютона может показаться, что он противоречит первому закону Ньютона. В самом деле, силы действия и противодействия равны по величине и направлены противоположно. Согласно первому закону Ньютона, скорость тела при этом должна оставаться постоянной. Причины для ускорения нет. Однако в первом законе Ньютона речь идет о результирующей всех сил, приложенных к одному и тому же телу, в то время как силы действия и противодействия приложены к разным телам, и поэтому не могут уравновесить друг друга.

3.5. Принцип относительности Галилея

Рассмотрим две системы отсчета, движущиеся друг относительно друга прямолинейно с постоянной скоростью (рис. 9). Связь между скоростями некоторой точки в этих системах дается выражением (14). Продифференцируем это соотношение по времени. Учитывая, что постоянна, получим:

или

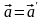. (35)

Отсюда следует, что ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, оказывается одним и тем же. Поэтому, если одна из этих систем инерциальна (это значит, что при отсутствии сил 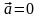), то и остальные будут инерциальными (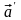 также равно нулю).

Величина, которая сохраняется при переходе от одной системы к другой, называется инвариантом. Таким образом, ускорение является инвариантом относительно преобразований Галилея.

Основное уравнение механики (31) характерно тем, что из кинематических величин оно содержит только ускорение, скорость же в него не входит. Однако, как мы установили выше, ускорение какого-либо тела в двух произвольно выбранных инерциальных системах отсчета k и k' одинаково. Отсюда согласно второму закону Ньютона вытекает, что силы, действующие на тело в системах k и k' , также будут одинаковы. Следовательно, уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой, т. е. инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. С механической точки зрения все инерциальные системы отсчета совершенно эквивалентны: ни одной из них нельзя отдать предпочтение перед другими. Практически это проявляется в том, что никакими механическими опытами, проведенными в пределах данной системы отсчета, нельзя установить, находится ли она в состоянии покоя или в состоянии равномерного и прямолинейного движения. Находясь, например, в вагоне поезда, движущегося без толчков прямолинейно и равномерно, мы, не выглянув в окно, не сможем определить, движется вагон или покоится. Свободное падение тел, движение брошенных нами тел и все другие механические процессы будут в этом случае происходить так же, как и в случае, если бы вагон был неподвижен.

Указанные обстоятельства были выяснены еще Галилеем. Положение о том, что все механические явления в различных инерциальных системах отсчета протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно, носит название принципа относительности Галилея.

Если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Принцип относительности Галилея утверждает полное равноправие всех инерциальных систем отсчета. Значит ли это, что одно и то же движение выглядит одинаково во всех инерциальных системах отсчета? Конечно, нет. Мы уже рассматривали пример с монетой, выпавшей из рук пассажира автобуса, который движется по дороге равномерно и прямолинейно, плавно и без толчков. Траектория этой монеты в разных инерциальных системах отсчета будет выглядеть по-разному. Дело в том, что кинематические уравнения (1) или (2) получаются в результате решения дифференциальных уравнений (30) или (31). А чтобы решить дифференциальное уравнение, необходимо задать начальные условия. В нашем примере необходимо задать координаты и скорость монеты в начальный момент времени. Для пассажира автобуса в момент t = 0, когда монета выпала из рук, горизонтальная скорость монеты равна нулю (V(0) = 0). Для наблюдателя, стоящего на улице, горизонтальная скорость монеты в этот момент равна скорости автобуса (V(0) = VA). Разные начальные условия приведут к различным выражениям для траектории в различных инерциальных системах отсчета.