57

Определение коэффициента поверхностного натяжения методом

Ребиндера_______________________________________________

- Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 23 . 1-

ОПределение коэффициента поверхностного натяжения методом Ребиндера

1. Цель работы:

1. Изучение методики определения коэффициента поверхностного натяжения жидкостей методом Ребиндера.

2. Исследование зависимости коэффициента поверхностного натяжения жидкостей от температуры.

3. Определение зависимости коэффициента поверхностного натяжения раствора от его концентрации.

2. Библиография:

1. Сивухин Д.В. Термодинамика и молекулярная физика: Учеб. пособие для вузов. - 3 -е изд., испр. и доп. - М.: Наука. гл. ред. физ. - мат. лит., 1990. - 592 с.-(Общий курс физики, т.2).

2. Ливенцев Н.М. Курс физики для медвузов. Учебник. Изд. 5-е, перераб. -М.:, Высш. шк., 1974. - 648 с.

3. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. - 2-е изд., перераб и доп. - М.: Высш. шк., 1990. - 478 с.

4. Эссаулова И.А. Руководство к лабораторным работам по медицинской и биологической физике: Учеб. Пособие для медвузов/Под ред. А.Н. Ремизова._М.: Высш. шк., 1987. - 271 с.

5. Майсова Н.Н. Практикум по курсу общей физики. - М.: Высш. шк., 1970.- 448 с

3. Теоретическое введение

1. Давление над искривленной поверхностью жидкости

Если поверхность жидкости не плоская, то она оказывает на жидкость избыточное давление, обусловленное силами поверхностного натяжения. Рассчитаем величину избыточного давления сферической поверхности жидкости радиуса (рисунок 1). На каждый малый элемент окружности АВ с центром в точке О₁ действует сила поверхностного натяжения , совпадающая по направлению с касательной к поверхности жидкости (касательная к сфере). Разложим силу на две составляющие и . Видно, что геометрическая сумма сил для рассматриваемой сферической поверхности равна нулю. Таким образом, давление искривленной поверхности жидкости обусловлено действующими составляющими силами

Рисунок 1

Результирующая всех этих сил равна алгебраической сумме составляющих :

. (1)

Рассчитаем величину избыточного давления. Для этого результирующую силу разделим на площадь основания шарового сегмента . Тогда получим:

. (2)

Если поверхность жидкости имеет произвольную форму , то избыточное давление определяется по формуле Лапласа:

, (3)

где и — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в данной точке.

При этом радиус кривизны положителен, если центр кривизны находится внутри жидкости и отрицателен, если центр расположен вне жидкости.

2. Описание установки и методика проведения эксперимента

Прибор для измерения поверхностного натяжения жидкостей методом максимального давления в пузырьке воздуха разработан академиком П.А. Ребиндером. Установка (рис.2) состоит из трубки Т, нижняя часть которой заканчивается капилляром радиуса . Трубка Т соединяется с водяным манометром М и резиновой грушей Г. Между манометром М и грушей Г находится кран К, позволяющий соединять грушу и левое колено манометра с атмосферой. Капилляр опускается в исследуемую жидкость на глубину нескольких мм. Открыв кран К, добиваются равновесия воды в коленах водяного манометра. Если осторожно нагнетать воздух грушей в капилляр, то на конце капилляра возникает пузырек воздуха (П). При этом давление в трубке возрастает, вода в правом колене поднимается, в левом опускается. В момент отрыва пузырька от капилляра устанавливается постоянное избыточное давление в манометре.

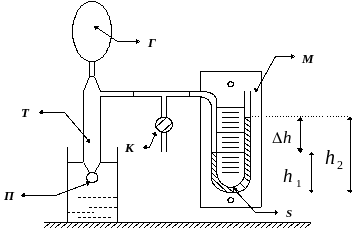
Рисунок 2

Введем следующие обозначения:

- давление в трубке в момент отрыва пузырька воздуха от капилляра;

- давление под криволинейной поверхностью пузырька, определяемое по формуле Лапласа

;

- атмосферное давление.

Тогда для капилляра можно записать условие отрыва пузырька от капилляра (условие равновесия):

. (4)

С другой стороны, равновесие мысленной площадки в нижней части водяного манометра наступает в том случае, когда давление, производимое на эту площадку слева ( ) будет равно давлению на эту же площадку справа ( ), т.е.

= . (5)

Если почленно из соотношения (5) вычесть уравнение (4), то получим следующее выражение:

. (6)

Отсюда

, (7)

где - разность высот воды в трубках водяного манометра.

Таким образом, коэффициент поверхностного натяжения может быть найден по формуле

. (8)

Отсюда можно определить радиус капилляра (воздушного пузырька)

. (9)

Поскольку непосредственное определение радиуса капилляра и, таким образом, радиуса пузырька воздуха затруднительно, то как правило используют относительный метод. Вначале проводят измерение для стандартной жидкости (эталона) с известным значением коэффициента поверхностного натяжения и плотности. В качестве такой стандартной жидкости удобно выбрать дистиллированную воду, коэффициент поверхностного натяжения и плотность которой представлены в таблице 1. Измерение избыточного давления водяного манометра для дистиллированной воды (эталона) выполняют при заданных условиях проведения эксперимента (температуре, атмосферном давлении). По

формуле (9) можно рассчитать радиус капилляра, который в дальнейшем используется при определении коэффициента поверхностного натяжения исследуемых жидкостей.

Плотность и поверхностное натяжение воды Таблица 1

T, 0С	, 103 кг/м3	, 10-3 Н/м	Примечание
0	0,99987	75,62
4	1,00000	75,06
6	0,99997	74,76
8	0,99988	74,48
10	0,99973	74,20
12	0,99953	73,92
14	0,99927	73,64
16	0,99897	73,34
18	0,99862	73,05
20	0,99823	72,75
22	0,99780	72,44
24	0,99733	72,12
30	0,99568	71,15
40	0,99225	69,55