Западно - Казахстанский государственный университет им. М. Утемисова

кафедра физики и математики

Проект

«Электрические явления в задачах электростатики»

Выполнено:

магистранты 2 курса

ИскалиеваА., Моисеева Н., Полежаева Г.

Руководитель:

Канд.ф.-м.наук, профессор

Кузьмичева А.Е.

Уральск – 2012г

Содержание:

Введение

1. Решение некоторых задач электростатики

1.1 Теорема Остроградского – Гаусса

1.2 Энергия электростатического поля.

1.3 Уравнения Пуассона и Лапласа

1.4 Метод изображений.

1.5 Конденсаторы

2. Рекомендуемые задачи (37 - 47)

Заключение

Список использованной литературы

Введение

Актуальность: Электрические явления определяются электромагнитным взаимодействием, относящимся к классу фундаментальных взаимодействий. Основными понятиями в теории этого взаимодействия являются заряд и поле. Раздел физики, изучающий неподвижный заряд и существование вокруг него поля – электростатика. Поля неподвижных зарядов имеют большое практическое значение. Поэтому решение задач электростатики является актуальным. Целью проекта является разработка цикла задач электростатики. Задачи:

- расчет электростатического поля различных систем неподвижных зарядов различными методами;

- расчет энергии электростатического поля;

- расчет электроемкости конденсаторов.

Практическая значимость работы: использование разработанных материалов в учебном процессе вуза и в классах физико – математического профиля.

1. Решение некоторых задач электростатики

1.1 Теорема Остроградского – Гаусса

1. Используя теорему Остроградского-Гаусса определить напряженность электростатического поля, создаваемого двумя бесконечными равнозаряженными пластинами. Плотность заряда σ. Знак зарядов пластин одинаковый.

2. Используя теорему Остроградского-Гаусса определить напряженность электростатического поля, создаваемого двумя бесконечными равнозаряженными пластинами. Плотность заряда σ. Знак зарядов пластин различный.

3. Используя теорему Остроградского-Гаусса определить напряженность электростатического поля, создаваемого двумя бесконечными длинными тонкими цилиндрами. Поверхностная плотность заряда σ, по знаку одинакова.

4. Используя теорему Остроградского-Гаусса определить напряженность электростатического поля, создаваемого двумя бесконечными длинными тонкими цилиндрами. Поверхностная плотность заряда σ, по знаку различна.

5. Используя теорему Остроградского-Гаусса определить напряженность электростатического поля, создаваемого двумя концентрическими сферами радиуса R₁ и R₂. Заряд сфер q одинаков по знаку, равномерно распределены по поверхность.

6. Используя теорему Остроградского-Гаусса определить напряженность электростатического поля, создаваемого двумя концентрическими сферами радиуса R₁ и R₂. Заряд сфер противоположны по знаку, равномерно распределены по поверхность.

7. Объемная плотность заряда равномерно заряженного шара радиусом R=6 см, изготовленного из диэлектрика с проницаемостью =2, равна ρ=6,7·10^-6 Кл/м³ . Найти напряженность Е электрического поля на расстоянии r₁=3 см и r₂= 9 см от центра шара, считая, что относительная диэлектрическая проницаемость среды, в которой находится шар, равна =3. Построить график зависимости напряженности поля как функции расстояния от центра шара.

Дано: R= Найти:

Анализ и решение:

Использованием теорему Остроградского-Гаусса. Построим вспомогательную замкнутую

поверхность через точку 1 и 2 в форме прямого цилиндра

S - воображаемая поверхность, q – заряд внутри поверхности S.

1. Строим поверхность, проходящую через точку 1 с центром в центре шара. В силу симметрии заряда

-объем, ограниченный поверхностью

Е – одинаково во всех точках поверхности можно вынести за интеграл

2. Точка 2. S через точку 2, внутри нее весь заряженный шар

Если

Внутри шара Е растет по закону прямой пропорциональности, на границе . В среде в 3/2=1,5 раза, следовательно, в среде у поверхности Е_ср будет в 1,5 раза меньше, следовательно, на поверхности будет разрыв. При Е убывает пропорционально .

Ответ:

8. Объемная плотность заряда бесконечного равномерно заряженного слоя толщиной d = 20 см, изготовленного из диэлектрика проницаемостью , равна . Найти напряженность Е электрического поля в точках, находящихся на расстояниях и от середины слоя, и разность потенциалов между этими точками.

Использованием теорему Остроградского-Гаусса. Построим вспомогательную замкнутую

поверхность через точку 1 и 2 в форме прямого цилиндра

плоскости вследствие симметрии.

линии скользят по боковой поверхности, потока нет.

площадь правого и левого оснований.

Для внутренней поверхности

Для точки 2:

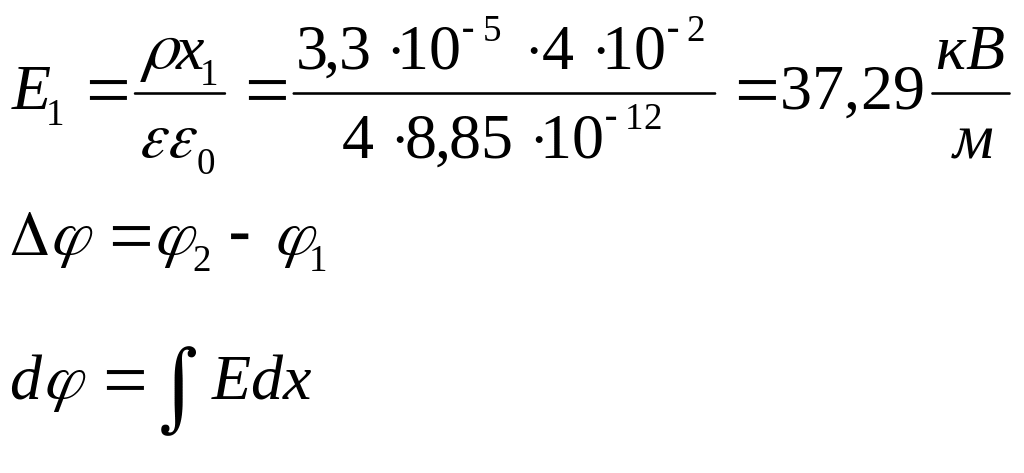
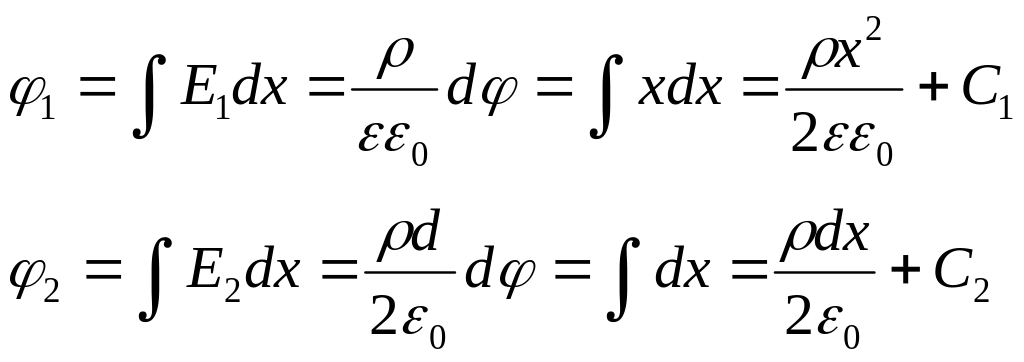
Для определения и нормируем потенциал.

Считаем: х=0 (центр плоскости) . Потенциал непрерывен (граница плоскости)

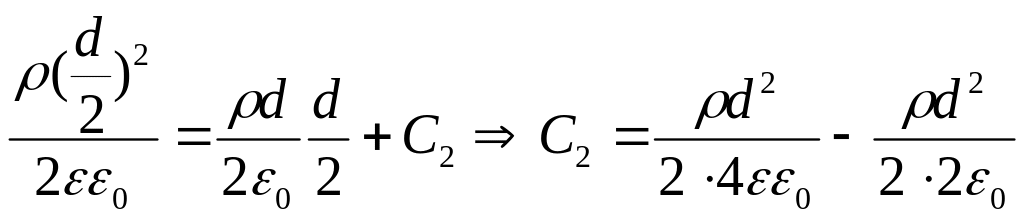
Ответ: , ,

9. Электроды двухэлектродной лампы имеют форму нити радиуса а=0,100 мм (катод) и коаксиального с ней цилиндра радиуса b=2,72 мм (анод). На электроды подано напряжение U=100 В. Определить силу, которая будет действовать на электрон, находящийся на расстоянии r=1,00 мм от оси катода.

Дано: Найти: F

Анализ и решение:

E – внутри цилиндра. Внутри такой лампы электрическое поле создает только нить (катод). Внешний цилиндр создает поле только вне лампы. Е нити можно найти по теореме Остроградского-Гаусса, или взять готовую из учебника

, - расстояние от оси, - заряд, приходящийся на единицу длины нити (он не дан).

Ответ: