Содержание

Введение 2

Задача 1 3

Задача 2 6

Задача 3 7

Задача 4 9

Задача 5 10

Задача 6 13

Заключение 16

Список литературы: 17

Введение

В повседневной жизни приходится постоянно сталкиваться с обслуживанием, то есть удовлетворением некоторых потребителей и очень часто с очередями, когда обслуживание является массовым. Примером процессов массового обслуживания может служить продажа билетов в железнодорожных, театральных и других кассах. Обслуживание бригадой рабочих группы станков, осуществление телефонной связи и так далее. Естественно, что во всех случаях большое значение имеет степень удовлетворения потребности в обслуживании или качество обслуживания. Так, при осуществлении телефонной связи важно знать, как долго придется ожидать соединения с требуемым объектом после заказа междугороднего разговора при ручном способе установления соединения и тому подобное. Предметом теории телетрафика является количественная сторона процессов обслуживания потоков сообщений в системах распределения информации. Данная курсовая работа предусматривает решение типичных задач.

Задача 1

На коммутационную систему поступает поток вызовов, создающий нагрузку Y Эрл. Определить вероятности поступления ровно i вызовов P_i (i=0,1,2,3,…,N) при примитивном потоке от N источников и P_i (i=0,1,2,3,…,j…) при простейшем потоке вызовов. Построить кривые распределения вероятностей P_i= f(i) и произвести сравнение полученных результатов.

Исходные данные:

Y=3.6 Эрл; N=8;

Решение:

Под потоком вызовов понимается последовательность вызовов, поступающих через какие-либо промежутки или в какие-либо моменты времени.

Простейший поток вызовов - это ординарный, стационарный поток без последействия.

Примитивным потоком называется такой симметричный поток, параметр которого - _i прямо пропорционален числу свободных в данный момент источников:

_i=(n-i) ,

где: i – число занятых источников;

 - параметр потока одного свободного источника.

Частным случаем примитивного потока является простейший поток вызовов. Параметр  простейшего потока вообще не зависит от состояния КС и для данного потока является величиной постоянной.

1)Простейший поток вызовов.

Математической моделью простейшего потока вызовов является формула Пуассона:

Она определяет вероятность поступления точно i вызовов при простейшем потоке с параметром 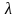за интервал времени t. Если мы возьмём t=1 (единичный интервал) то формула Пуассона примет вид:

Интенсивность простейшего потока вызовов количественно совпадает с его параметром, т.е.

. Величину поступающей нагрузки определим по формуле . Учитывая, что t=1 и , параметр численно совпадает c величиной поступающей нагрузки или .

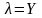Определим по формуле вероятность поступления вызовов простейшего потока.

;

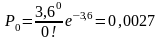
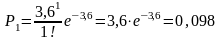
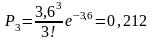
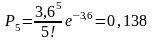
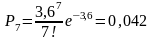
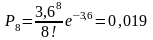
2)Примитивный поток вызовов.

При примитивном потоке от N источников вероятность поступления точно i вызовов определяется по формуле Бернулли:

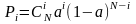
- удельная нагрузка от одного источника,

N – число источников,

i- число поступивших вызовов;

Определим вероятность , а остальные вероятности определим по первой рекуррентной формуле:

, где = =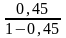0,818

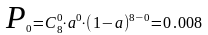
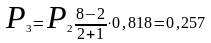
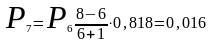
Мы получили , что соответствует действительности, поскольку мы имели дело с полной группой событий.

3)Кривые распределения вероятностей P_i= f(i).

Р_i

Строим кривые распределения вероятностей Р_i = f (i):

Рисунок 1 – Кривые распределения вероятностей при простейшем и примитивном потоках вызовов

Вывод:

Мы получили , что соответствует действительности, поскольку мы имели дело с полной группой событий. 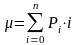=3,6, т.е. интенсивность поступающей нагрузки, выраженная в Эрл численно совпадает со средним числом вызовов за единичный интервал времени. Поэтому перегиб на графиках P_i= f(i) находится в точке i=Y=3,6