
- •Часть 2 «Электромагнетизм»
- •1 Магнитное поле в вакууме
- •1.1 Магнитное поле и его характеристики
- •Магнитного поля прямолинейного тока и правило правой руки
- •1.2 Закон Ампера
- •1. 3 Рамка с током в однородном магнитном поле
- •1.4 Закон Био – Савара – Лапласа и его применение к расчету магнитного поля
- •1.4.1 Магнитное поле в центре кругового проводника с током
- •1.4.2 Магнитное поле прямолинейного проводника с током
- •1.5 Взаимодействие двух параллельных проводников с током
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •2.2 Движение заряженной частицы в однородном постоянном электрическом поле
- •2.3 Движение заряженной частицы в однородном постоянном магнитном поле
- •2.4 Практические применения силы Лоренца. Эффект Холла
- •2.5 Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора в)
- •2.6 Магнитные поля соленоида и тороида
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •3 Явление электромагнитной индукции
- •3.1 Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля
- •3.2 Основной закон электромагнитной индукции
- •3.3 Явление самоиндукции
- •3.4 Явление взаимной индукции
- •3.5 Энергия магнитного поля
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •4 Электромагнитные колебания
- •4.1 Электрический колебательный контур. Формула Томсона
- •4.2 Свободные затухающие колебания. Добротность колебательного контура
- •4.3 Вынужденные электрические колебания. Метод векторных диаграмм
- •4.4 Резонанс напряжений и резонанс токов
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
1.2 Закон Ампера
В 1820 г. А.
Ампер установил, что сила, с которой
магнитное поле действует на элементарный
проводник с током I и
длиной
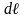 :
:
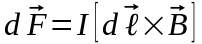 .
.
Вектор
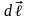 совпадает по направлению с током. Данная
формула выражает закон Ампера: сила,
действующая на элемент проводника с
током в магнитном поле, равна произведению
силы тока на векторное произведение
элемента длины проводника и магнитной
индукции поля.
совпадает по направлению с током. Данная
формула выражает закон Ампера: сила,
действующая на элемент проводника с
током в магнитном поле, равна произведению
силы тока на векторное произведение
элемента длины проводника и магнитной
индукции поля.
Е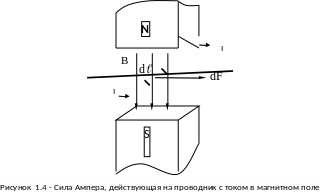 сли
поместить проводник с током между
полюсов постоянного магнита, то сила
Ампера будет действовать на него в
направлении, показанном на рис. 1.4.
сли
поместить проводник с током между
полюсов постоянного магнита, то сила
Ампера будет действовать на него в
направлении, показанном на рис. 1.4.
Направление
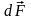 может быть найдено по правилу
левой руки: если ладонь левой руки
расположить так, чтобы вектор
был направлен в ладонь, а четыре вытянутых
пальца указывали направление тока в
проводнике, то отставленный под прямым
углом большой палец укажет
направление силы, действующей на
элемент проводника с током (рис.1.5).
может быть найдено по правилу
левой руки: если ладонь левой руки
расположить так, чтобы вектор
был направлен в ладонь, а четыре вытянутых
пальца указывали направление тока в
проводнике, то отставленный под прямым
углом большой палец укажет
направление силы, действующей на
элемент проводника с током (рис.1.5).
Модуль силы
Ампера вычисляется по формуле
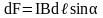 ,
где α – угол между векторами
и
.
Чтобы найти силу, действующую на проводник
конечной длины
в магнитном поле, необходимо определить
геометрическую сумму сил, действующих
на все малые элементы данного проводника,
,
где α – угол между векторами
и
.
Чтобы найти силу, действующую на проводник
конечной длины
в магнитном поле, необходимо определить
геометрическую сумму сил, действующих
на все малые элементы данного проводника,
т.е.
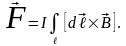
И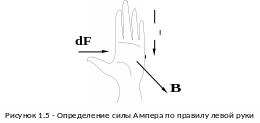 з
закона Ампера следует, что магнитные
силы нецентральные, так как они направлены
перпендикулярно силовым линиям магнитного
поля. Напомним, что электростатические
силы – центральные.
з
закона Ампера следует, что магнитные
силы нецентральные, так как они направлены
перпендикулярно силовым линиям магнитного
поля. Напомним, что электростатические
силы – центральные.
Закон
Ампера позволяет определить единицу
магнитной индукции В.
Предположим,
что элемент проводника dl
с током I
перпендикулярен направлению магнитного
поля. Тогда закон Ампера запишется в
виде dF
= IBdl,
откуда
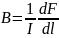 .
.
Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А: 1 Тл = 1 Н/(А м).
1. 3 Рамка с током в однородном магнитном поле
При исследовании
магнитного поля часто используется
замкнутый плоский контур с током (рамка
с током), линейные размеры которого малы
п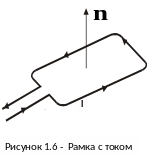 о
сравнению с расстоянием до токов,
образующих данное поле. Ориентация
контура в пространстве определяется
направлением нормали к контуру (рис.1.6).
Нормаль строится по правилу правого
винта: если головку винта вращать в
направлении тока, то движение его острия
совпадает с направлением n.
На каждый элемент тока в рамке действует
сила Ампера, и под действием этой силы
магнитное поле поворачивает рамку таким
образом, чтобы нормаль к ней располагалась
вдоль линий магнитной индукции В. Кстати,
так же располагается и стрелка компаса
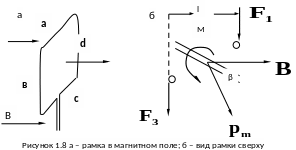
(рис.1.7). Рассчитаем силы, действующие
на каждую из четырех сторон рамки. Для
простоты будем считать, что стороны в
и d перпендикулярны
В (рис.1.8 а). Силы
о
сравнению с расстоянием до токов,
образующих данное поле. Ориентация
контура в пространстве определяется
направлением нормали к контуру (рис.1.6).
Нормаль строится по правилу правого
винта: если головку винта вращать в
направлении тока, то движение его острия
совпадает с направлением n.
На каждый элемент тока в рамке действует
сила Ампера, и под действием этой силы
магнитное поле поворачивает рамку таким
образом, чтобы нормаль к ней располагалась
вдоль линий магнитной индукции В. Кстати,
так же располагается и стрелка компаса
(рис.1.7). Рассчитаем силы, действующие
на каждую из четырех сторон рамки. Для
простоты будем считать, что стороны в
и d перпендикулярны
В (рис.1.8 а). Силы
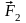 и
и
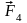 ,
приложенные к проводникам а и с,
численно равны и
,
приложенные к проводникам а и с,
численно равны и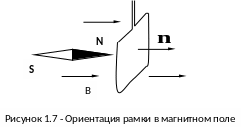 направлены вдоль вертикальной оси рамки
в противоположные стороны, поэтому они
полностью уравновешивают друг друга:
F2 =F4=IaB.
Силы
направлены вдоль вертикальной оси рамки
в противоположные стороны, поэтому они
полностью уравновешивают друг друга:
F2 =F4=IaB.
Силы
 и
и
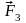 ,
действующие на прямолинейные проводники
в и d, направлены
перпендикулярно плоскости рисунка в
противоположные стороны (на рис.1.8 б
показан вид рамки сверху) и по закону
Ампера численно равны:
,
действующие на прямолинейные проводники
в и d, направлены
перпендикулярно плоскости рисунка в
противоположные стороны (на рис.1.8 б
показан вид рамки сверху) и по закону
Ампера численно равны:
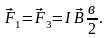 Силы
и
создают вращающий момент
Силы
и
создают вращающий момент
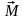 ,
который поворачивает рамку. Модуль
этого вектора М = 2F1l,
где l = аsinβ
(β – угол между направлением
магнитной индукции поля В и нормалью к
рамке). Воспользовавшись вышеприведенным
выражением для силы F1,
получим М = 2Ia
,
который поворачивает рамку. Модуль
этого вектора М = 2F1l,
где l = аsinβ
(β – угол между направлением
магнитной индукции поля В и нормалью к
рамке). Воспользовавшись вышеприведенным
выражением для силы F1,
получим М = 2Ia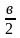 Вsinβ
= ISBsinβ, где S
= a в- площадь рамки.
Вsinβ
= ISBsinβ, где S
= a в- площадь рамки.
Данную формулу можно преобразовать, введя понятие магнитного момента
рамки с током (или контура с током).
Магнитным моментом
плоского замкнутого контура с током I
называется вектор
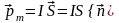 ,
где S – площадь поверхности, ограниченной
контуром;
,
где S – площадь поверхности, ограниченной
контуром;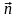 –
единичный вектор нормали к плоскости
контура.
–
единичный вектор нормали к плоскости
контура.
Векторы
 направлены перпендикулярно плоскости
контура так, что из их концов ток в
контуре виден идущим против часовой
стрелки (рис.1.9). Для момента сил получаем
направлены перпендикулярно плоскости
контура так, что из их концов ток в
контуре виден идущим против часовой
стрелки (рис.1.9). Для момента сил получаем
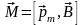 ,
модуль момента сил будет равен М = рmBsinβ
.
,
модуль момента сил будет равен М = рmBsinβ
.
Е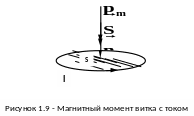 сли
в данную точку магнитного поля помещать
рамки с различными магнитными моментами,
то на них действуют различные вращающие
моменты, однако отношение Mmax/pm
(Мmax
— максимальный вращающий момент) для
всех контуров одно и то же и поэтому
может служить характеристикой магнитного
поля, называемой магнитной индукцией:
сли
в данную точку магнитного поля помещать
рамки с различными магнитными моментами,
то на них действуют различные вращающие
моменты, однако отношение Mmax/pm
(Мmax
— максимальный вращающий момент) для
всех контуров одно и то же и поэтому
может служить характеристикой магнитного
поля, называемой магнитной индукцией:
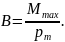
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля.
Действие магнитного поля на рамку с током широко применяется в электроизмерительных приборах. Работа любого прибора магнитоэлектрической системы (например, зеркального гальванометра) основана на взаимодействии магнитного поля постоянного магнита и рамки с током. Как известно, в данном случае возникает вращающий момент, который будет поворачивать рамку. Угол поворота рамки и связанные с ним показания шкалы прибора будут зависеть от силы тока в рамке. Такие гальванометры могут измерять постоянные токи порядка 10 А.
