
- •Часть 2 «Электромагнетизм»
- •1 Магнитное поле в вакууме
- •1.1 Магнитное поле и его характеристики
- •Магнитного поля прямолинейного тока и правило правой руки
- •1.2 Закон Ампера
- •1. 3 Рамка с током в однородном магнитном поле
- •1.4 Закон Био – Савара – Лапласа и его применение к расчету магнитного поля
- •1.4.1 Магнитное поле в центре кругового проводника с током
- •1.4.2 Магнитное поле прямолинейного проводника с током
- •1.5 Взаимодействие двух параллельных проводников с током
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •2.2 Движение заряженной частицы в однородном постоянном электрическом поле
- •2.3 Движение заряженной частицы в однородном постоянном магнитном поле
- •2.4 Практические применения силы Лоренца. Эффект Холла
- •2.5 Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора в)
- •2.6 Магнитные поля соленоида и тороида
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •3 Явление электромагнитной индукции
- •3.1 Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля
- •3.2 Основной закон электромагнитной индукции
- •3.3 Явление самоиндукции
- •3.4 Явление взаимной индукции
- •3.5 Энергия магнитного поля
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •4 Электромагнитные колебания
- •4.1 Электрический колебательный контур. Формула Томсона
- •4.2 Свободные затухающие колебания. Добротность колебательного контура
- •4.3 Вынужденные электрические колебания. Метод векторных диаграмм
- •4.4 Резонанс напряжений и резонанс токов
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
Примеры решения задач
Задача 1. Виток, по которому течет ток I=20А, свободно установился в однородном магнитном поле В = 16 мТл. Диаметр d витка равен 10 см. Какую работу нужно совершать, чтобы медленно повернуть виток на угол α = относительно оси, совпадающей с диаметром?
Решение: При медленном повороте контура в магнитном поле индукционными токами можно пренебречь и считать ток в контуре неизменным. Работа сил в этом случае определяется выражением
А = I(Φ2 - Φ1).
где Φ1 и Φ2 – магнитные потоки, пронизывающие контур в начальном и конечном положениях.
Работа внешних сил будет равна по модулю работе сил поля и противоположна ей по знаку, т.е.
Авн = I(Φ1 – Φ2).
Так
как в начальном положении контур
установился свободно (положение
устойчивого равновесия), то момент
внешних сил, действующий на контур,
равен нулю. В этом положении вектор
магнитного момента
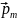 контура
сонаправлен с вектором
(рис. 3.7 а) и магнитный поток Φ1
максимален (α=0, cosα
= 1), т.е. Φ1=BS
(где S
– площадь контура). В конечном положении
(рис. 3.7 б) вектор
перпендикулярен вектору
(
контура
сонаправлен с вектором
(рис. 3.7 а) и магнитный поток Φ1
максимален (α=0, cosα
= 1), т.е. Φ1=BS
(где S
– площадь контура). В конечном положении
(рис. 3.7 б) вектор
перпендикулярен вектору
(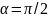 ,
,
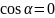 )
и
)
и


магнитный поток Φ2 = 0. Перепишем выражение работы внешних сил Авн с учетом сделанных замечаний:
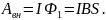
Так
как площадь контура
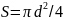 ,
то работа
,
то работа
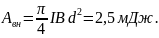
Задача
2. В однородном
магнитном поле с индукцией В = 0,1 Тл
равномерно вращается рамка, содержащая
N
= 1000 витков, с частотой
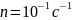 .
Площадь S
рамки равна 150 см2.
Определить мгновенное значение ЭДС
,
соответствующее углу поворота рамки
300.
.
Площадь S
рамки равна 150 см2.
Определить мгновенное значение ЭДС
,
соответствующее углу поворота рамки
300.
Решение: мгновенное значение ЭДС индукции определяется основным уравнением электромагнитной индукции Фарадея-Максвелла:
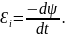
(1)
Потокосцепление ψ = NΦ, где N–число витков, пронизываемых магнитным потоком Φ. Подставив выражение ψ в формулу (1), получим:

(2)
При
вращении рамки магнитный поток Φ,
пронизывающий рамку в момент времени
t,
изменяется по закону
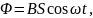 где B–магнитная
индукция; S–площадь
рамки; ω–циклическая
частота. Подставив в формулу (2) выражение
Φ
и продифференцировав по времени, найдем
мгновенное значение ЭДС индукции:
где B–магнитная
индукция; S–площадь
рамки; ω–циклическая
частота. Подставив в формулу (2) выражение
Φ
и продифференцировав по времени, найдем
мгновенное значение ЭДС индукции:

(3)
Циклическая
частота ω связана с частотой n
вращения соотношением
 Подставив выражение ω в формулу (3),
получим
Подставив выражение ω в формулу (3),
получим

Задача 3. В магнитном поле с индукцией В = 10-2 Тл вращается стержень длиной l = 0,2 м с постоянной угловой скоростью ω = 100 с-1. Найдите ЭДС индукции, возникающую в стержне, если ось вращения проходит через конец стержня параллельно линиям индукции магнитного поля.
Решение: Согласно закону электромагнитной индукции на концах стержня возникает постоянная разность потенциалов, равная
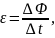
где
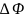 – магнитный поток, проходящий через
поверхность, описываемую стержнем за
время
– магнитный поток, проходящий через
поверхность, описываемую стержнем за
время
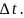
При
вращении стержня под прямым углом к
линиям индукции магнитного поля
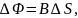 где
где
 – площадь сектора, описываемого стержнем.
– площадь сектора, описываемого стержнем.
За
время
стержень поворачивается на угол
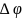 ,
и площадь сектора равна
,
и площадь сектора равна
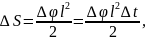 так как
так как
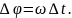
Следовательно, изменение магнитного потока равно
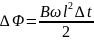
и

Задача 4. По соленоиду течет ток I = 2 А. магнитный поток Φ, пронизывающий поперечное сечение соленоида, равен 4∙10-6 Вб. Определить индуктивность L соленоида, если он имеет N = 800 витков.
Решение: Индуктивность L соленоида связана с потокосцеплением ψ соотношением ψ = LI, откуда L = ψ/I. Заменив здесь потокосцепление ψ его выражением через магнитный поток Φ и число витков N соленоида (ψ = ΦN), получим

Задача 5. При скорости изменения силы тока ΔI/Δtв соленоиде, равной 50 А/с, на его концах возникает ЭДС самоиндукции = 0,08 В. Определить индуктивность L соленоида.
Решение: Индуктивность соленоида связана с ЭДС самоиндукции и скоростью изменения силы тока в его обмотке соотношением
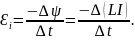
Вынося постоянную величину L за знак приращения, получим
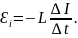
Опустив знак минус в этом равенстве (направление ЭДС в данном случае несущественно) и выразив интересующую нас величину - индуктивность, получим

Задача 6. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода диаметром d = 0,2 мм. Диаметр D соленоида равен 5 см. по соленоиду течет ток I = 1 А. Определить количество электричества Q, протекающее через обмотку, если концы ее замкнуть накоротко. Толщиной изоляции пренебречь.
Решение: Возможны два способа решения.
1-й способ. Количество электричества dQ, которое протекает по проводнику за время dt при силе тока I, определяется равенством
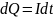
(4)
. Полное
количество электричества, протекающее
через проводник за время t,
будет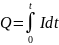 .
Сила тока в данном случае убывает
экспоненциально со временем и выражается
формулой
.
Сила тока в данном случае убывает
экспоненциально со временем и выражается
формулой
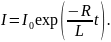
В
.
нося выражение силы тока I под знак интеграла и интегрируя от 0 до ∞ (при t→ ∞ I→ 0), получим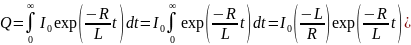
Подставим пределы интегрирования и определим количество электричества, протекающее через обмотку:

(5)
2-й
способ. Подставив
в формулу (4) вместо силы тока I
выражение ее через ЭДС индукции
и сопротивление R
соленоида, т.е. I
=
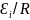 ,
найдем
,
найдем
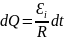 .
.
Но
сязана со скоростью изменения
потокосцепления ψ по закону
Фарадея-Максвелла:
 тогда
тогда

Интегрируя, получаем

(6)
Потокосцепление
ψ пропорционально силе тока в соленоиде.
Следовательно,
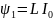 ;
ψ2
= 0, так как ψ2
соответствует
тому моменту, когда ток в цепи обратится
в нуль. Подставив выражения ψ1
и ψ2в
формулу (6), получим Q
= ψ1/R,
или
;
ψ2
= 0, так как ψ2
соответствует
тому моменту, когда ток в цепи обратится
в нуль. Подставив выражения ψ1
и ψ2в
формулу (6), получим Q
= ψ1/R,
или

что совпадает с формулой (5).
Для определения заряда, протекающего через обмотку соленоида, следует найти индуктивность L соленоида и сопротиивление R обмотки соленоида, которые выражаются формулами
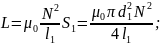
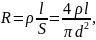
где
-магнитная постоянная; N
– число витков; l1–длина
соленоида; S1–площадь
сечения соленоида;
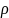 – удельное сопротивление провода;
l–длина
провода; S
– площадь сечения провода; d–диаметр
провода; d1–диаметр
соленоида.
– удельное сопротивление провода;
l–длина
провода; S
– площадь сечения провода; d–диаметр
провода; d1–диаметр
соленоида.
Подставив найденные выражения L и R в формулу (5), получим
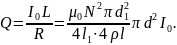
(6)
Заметим, что длина провода l может быть выражена через диаметр d1, соленоида соотношением l = πd1N, где N – число витков, тогда формуле (6) можно придать вид
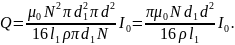
Но l1/N есть диаметр провода, так как витки плотно прилегают друг к другу. Следовательно,

Вывод: Очень важно при анализе задач учитывать всю совокупность явлений, связанных с возникновением тока индукции, его взаимодействием с магнитным полем и влиянием на условия, вызвавшие его появление.
