3.3. Построение тени от точки и прямой на поверхность другого предмета

3.3.1. Построить падающую тень от точки А и вертикального стержня АВ, точка В которого расположена на предметной плоскости Т. При центральном освещении заданы перспективы источника освещения L_К и его вторичной проекции L_КВ . Плоскость Σ Т задана в виде прямоугольника своей перспективой Σ_К , нижняя сторона которого расположена на плоскости Т .

3.3.2. Построить падающую тень от точки А и вертикального стержня АВ , точка В которого лежит на предметной плоскости Т . При параллельном освещении слева заданы направления лучей света r и их вторичных проекций r_Т . Плоскость Σ на пути потока лучей света наклонена к предметной плоскости Т и задана перспективой Σ_К в виде прямоугольника, нижняя сторона которого лежит на плоскости Т .

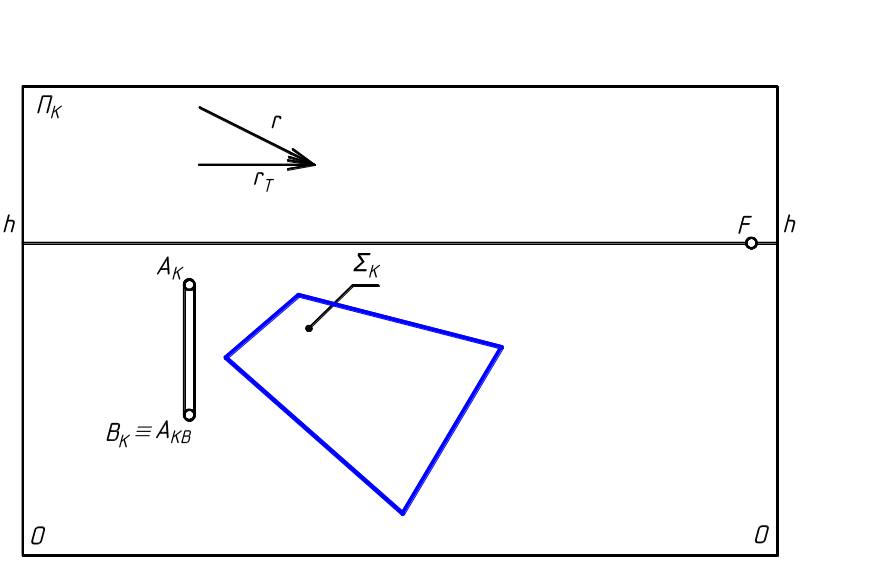
3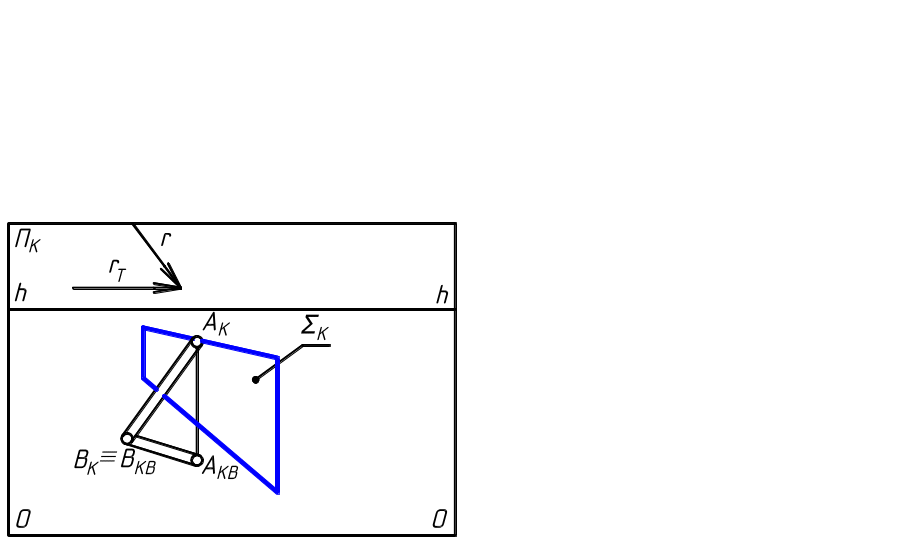 .3.3. Построить падающую тень от точки А и наклонённого к предметной плоскости Т стержня АВ , точка В которого расположена на плоскости Т . При параллельном освещении слева заданы направление лучей света r и их вторичных проекций r_Т . Плоскость Σ Т , расположенная на пути потока лучей света, задана своей перспективой Σ_К в виде прямоугольника, нижняя сторона которого лежит на плоскости Т .

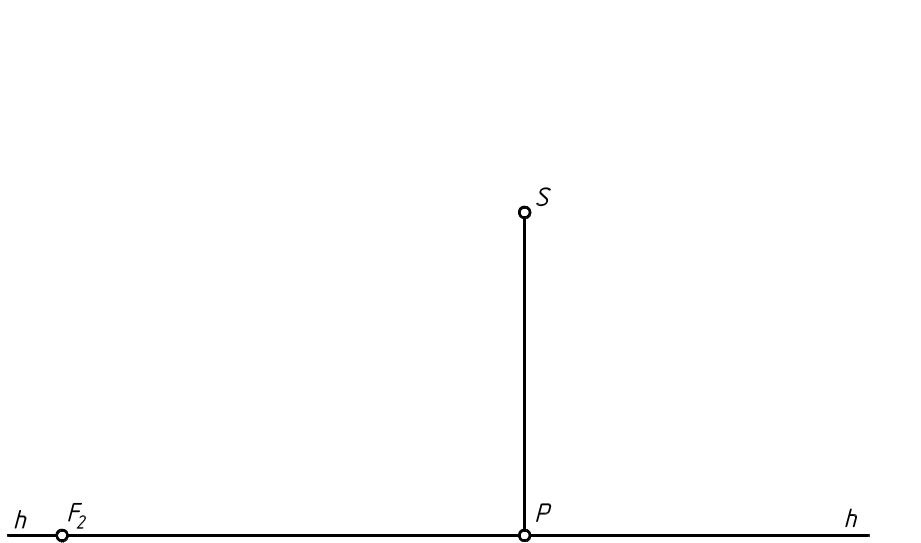
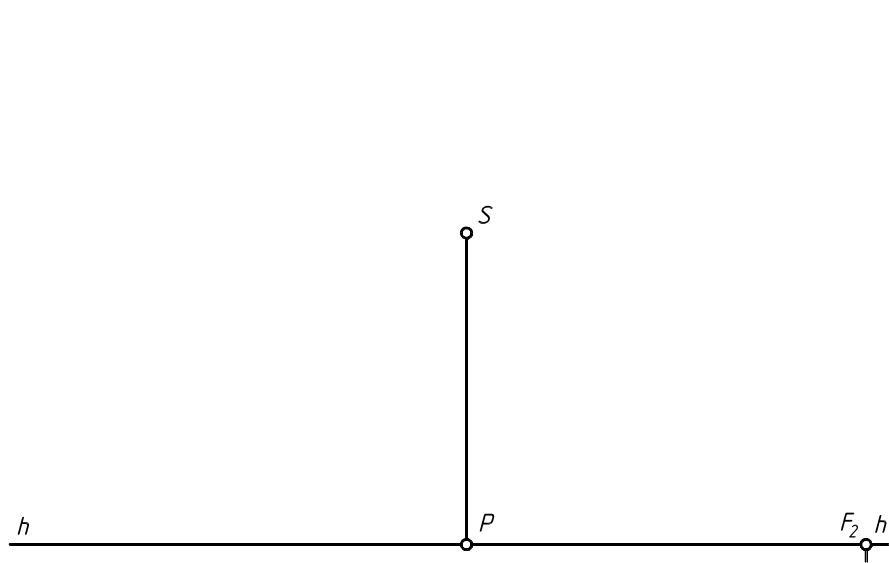
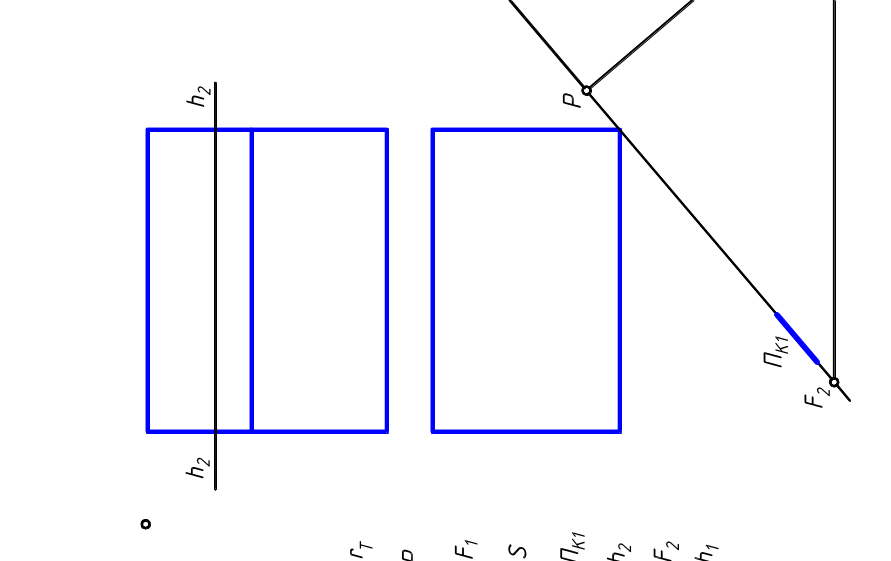
3.3.4. Построить падающую тень от точки А и наклонённого к предметной плоскости Т стержня АВ , точка В которого расположена на плоскости Т. При параллельном освещении сзади слева заданы точки схода F₁ и F₂ перспектив лучей света и их вторичных проекций. Плоскость Σ , расположенная на пути потока лучей света, наклонена к плоскости Т и задана своей перспективой Σ_К в виде прямоугольника, нижняя сторона которого лежит на плоскости Т .

Задание на дом:

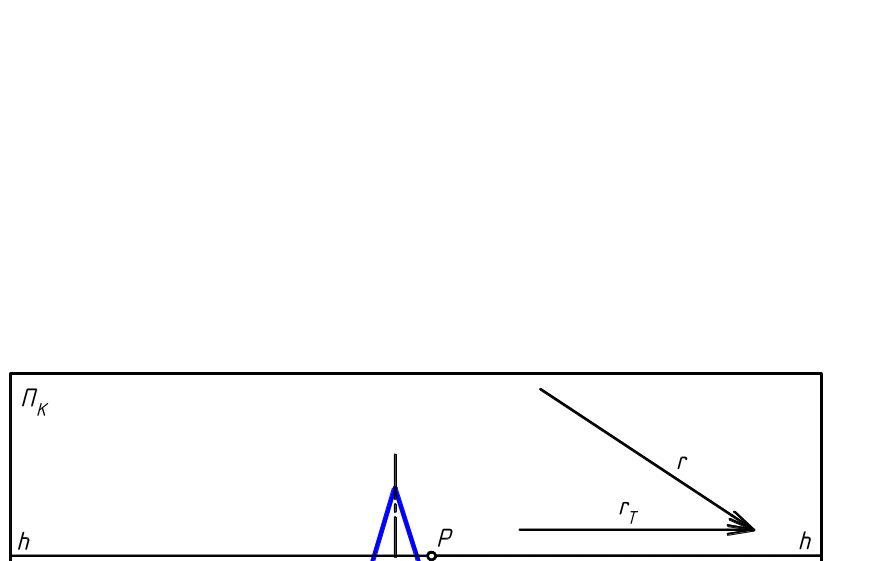
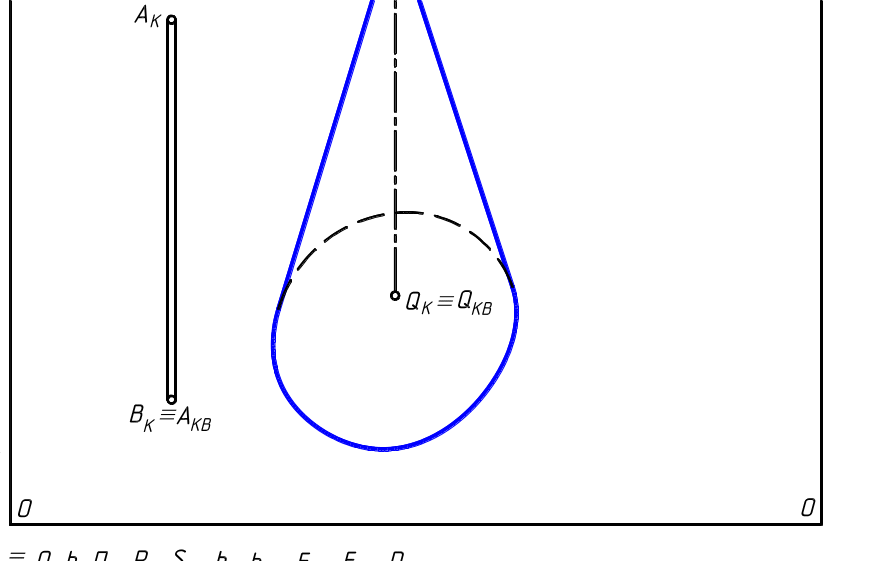
3.3.5. На перспективном изображении прямого кругового конуса найти падающую тень от точки А и вертикального стержня АВ, точка В которого лежит на предметной плоскости Т .

На картинной плоскости П_К заданы направления лучей света r и их вторичных проекций r_Т при параллельном освещении слева.

3.3.6. На перспективном изображении прямого кругового цилиндра найти падающую тень от стержня а, заданного перспективами а_К и а_КВ самого стержня и его вторичной проекции.

На картинной плоскости П_К заданы перспективы L_К и L_КВ источника освещения L и его вторичной проекции при центральном освещении.

4. Построение рисунка пространственного объекта в перспективе

4.1. Рисунок объекта в виде геометрической фигуры

4.1.1. Построить перспективу прямого параллелепипеда с нижним основанием в виде прямоугольника АВСЕ, произвольно расположенным на предметной плоскости, с помощью способа перспективных масштабов. Принять следующие размеры параллелепипеда: длина (сторона АВ) – 600мм, ширина (сторона АЕ) – 400мм, высота (сторона АА) – 700мм.

Построить также перспективу собственной и падающей тени, если заданы точки схода F₁ и F₂ перспектив параллельных лучей света и их вторичных проекций.

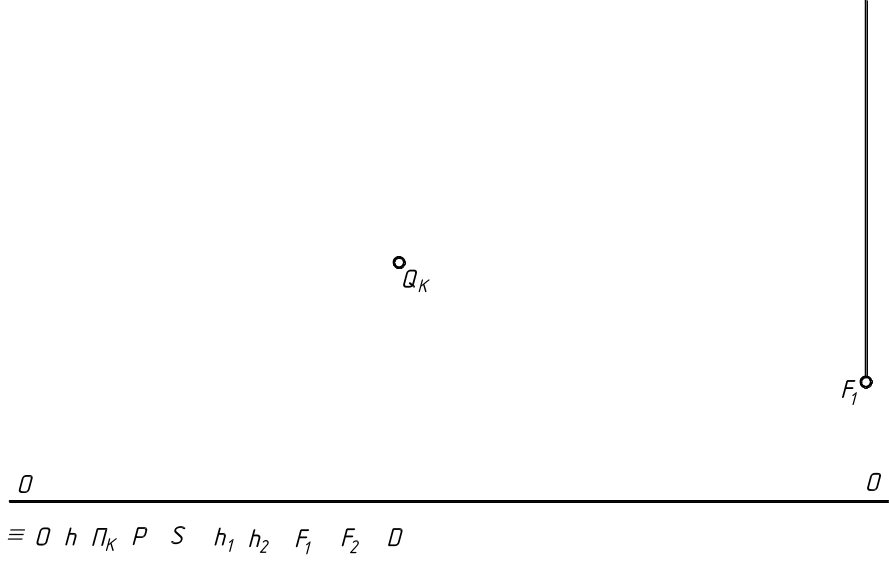
4.1.2. Построить перспективу прямого кругового цилиндра с нижним основанием, лежащим на предметной плоскости, с помощью способа перспективных масштабов, если на картинной плоскости П_К задана перспектива Q_К центра окружности нижнего основания, а высота цилиндра – 800мм.

Принять диаметр окружности основания равным 800мм. Построить также перспективу собственной и падающей тени, если заданы точки схода F₁ и F₂ перспектив параллельных лучей света.

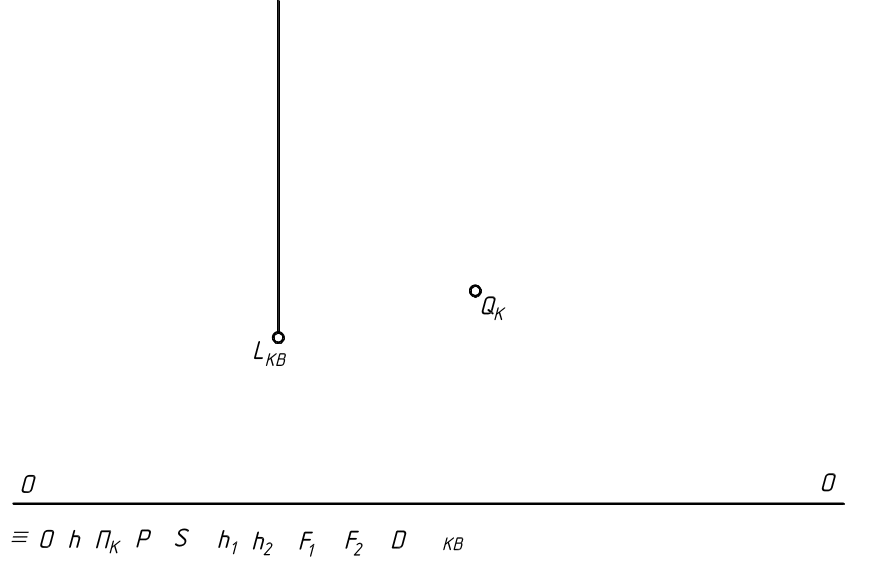
4.1.3. Построить перспективу прямого кругового конуса с нижним основанием, расположенным на предметной плоскости, с помощью способа перспективных масштабов, если на картинной плоскости П_К задана перспектива Q_К центра окружности нижнего основания.

П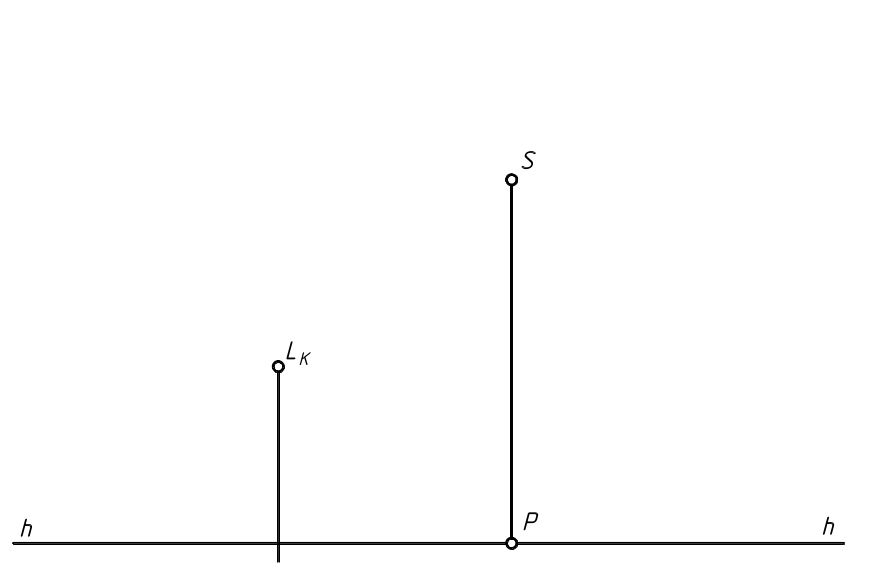 ринять диаметр окружности основа-ния равным 800мм, а высоту конуса – 1200мм. Построить также перспективу собственной и падаю-щей тени, если пер-спективы светящейся точки и её вторичной проекции централь-ного освещения – L_К и L_КВ .

Задание на дом:

4.1.4. Построить контуры собственной и падающей на опору тени от прямого кругового конуса на рисунке упражнения 3.3.5.

4.1.5. Построить контуры собственной и падающей на опору тени от прямого кругового цилиндра на рисунке упражнения 3.3.6.

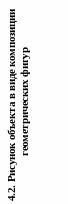EMBED AutoCAD.Drawing.16 EMBED AutoCAD.Drawing.16

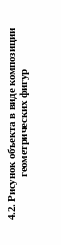
Задание на дом:

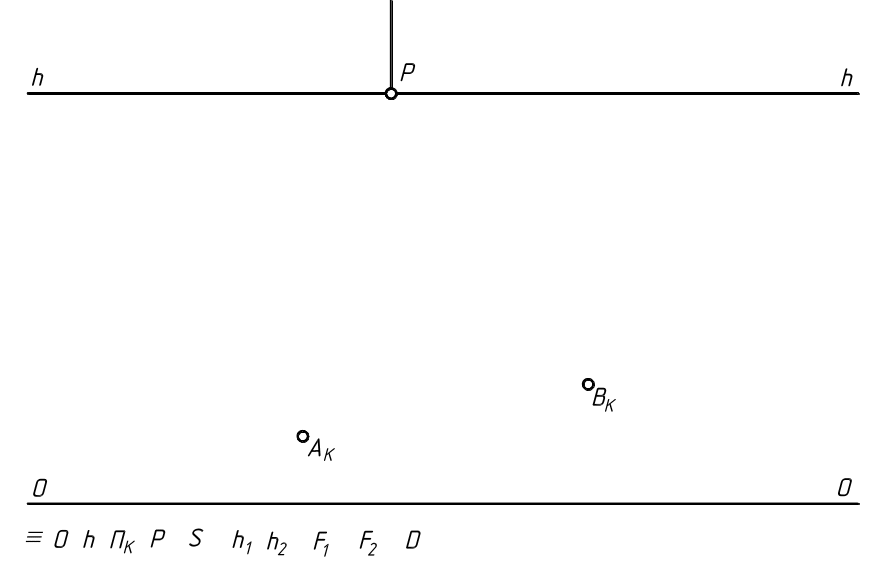
4.2.4. Построить перспективное изображение правильной четырёхгранной пирамиды и прямоугольного параллелепипеда, используя способ перспективных масштабов и масштабных точек. Основание пирамиды и нижнее основание параллелепипеда произвольно расположены на предметной плоскости Т .

На плоскости П_К заданы: перспектива А_К точки основания пирамиды, длина стороны которого равна 600мм; высота пирамиды – 1000мм; перспектива B_К точки нижнего основания (BFKM) параллелепипеда; длина основания параллелепипеда (сторона ВМ) равна 1100мм, ширина основания (сторона ВF) равна 400мм, высота параллелепипеда равна 400мм.

Построить также собственные и падающие тени при параллельном освещении, если r и r_Т соответственно - направления лучей света и их вторичных проекций.

УЧЕБНОЕ ИЗДАНИЕ

Никифоров Валерий Михайлович, к.т.н., профессор

Фатеев Виктор Иванович, к.т.н., доцент

РАБОЧАЯ ТЕТРАДЬ

ПО ПОСТРОЕНИЮ РИСУНКА

В ПЕРСПЕКТИВЕ

Усл.печ.л. Тираж _______экз. Заказ № _________

Редакционно-издательский отдел МГУДТ