Примеры решения задач

Пример 1. Ток силой 5 А течет по тонкому изогнутому проводнику (рис. 1.7). Радиус изогнутой части проводника 120 мм, угол 2=90^о. Найти магнитную индукцию в точке О.

Решение

Индукция магнитного поля в точке О является векторной суммой индукцийи, создаваемых током, протекающим по круговому и прямолинейному участкам проводника. Все элементы тока создают в точке О магнитные поля, векторы индукции которых направлены в одну сторону (перпендикулярно плоскости рисунка «от нас» правило правого винта). Поэтому от векторной суммы можно перейти к алгебраической, т.е.

В=В₁+В₂. (1)

Используя (1.1) и (1.4), найдем В₁ и В₂:

, (2)

. (3)

Объединяя (1), (2) и (3) и подставляя числовые значения, получим

Ответ: В = 28 мкТл.

Пример 2. Тонкий непроводящий диск радиусом R, равномерно заряженный с одной стороны с поверхностной плотностью , вращается вокруг своей оси с угловой скоростью . Найти: а) индукцию магнитного поля в центре диска;

б) магнитный момент диска.

Решение

Выделим на расстоянии r от центра диска кольцевую полоску шириной dr (рис. 1.8). На этой полоске находится заряд dq=dS=2rdr. Вследствие вращения данный заряд создает электрический круговой ток силой dI=dq=dq/2. Круговой ток создает в центре диска магнитное поле с индукцией B, которая может быть вычислена как индукция на оси кругового тока при х=0 (1.4):

.

Магнитный момент тока

.

Используя принцип суперпозиции и учитывая, что все элементарные кольцевые токи создают в центре диска магнитные поля одного направления, получим

,

.

Пример 3. По круглому однородному прямому проводу, радиус сечения которогоR, течет постоянный ток плотностью . Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиусом-вектором. Магнитную проницаемость всюду считать равной единице.

Решение

В данной задаче величина вектора зависит только от расстояния до оси провода, а сам вектор направлен по касательной к окружности, с центром на оси провода и проходящей через данную точку. Поэтому для решения задачи воспользуемся теоремой о циркуляции вектора

,

где I  сила электрического тока через поверхность контура интегрирования.

1. Выберем в качестве контура интегрирования L окружность радиусом rR, направление обхода контура свяжем с направлением вектора правилом правого винта (рис. 1.9).

.

Сила тока через поверхность круга радиусом r

.

По теореме о циркуляции

, .

Учитывая взаимную ориентацию векторов, получим, что вектор индукции магнитного поля внутри проводника с током равен:

.

2. При rR решение задачи аналогично предыдущему, за исключением того, что сила тока через поверхность контура будет постоянной и равной

.

Тогда

,

и в векторном виде

.

П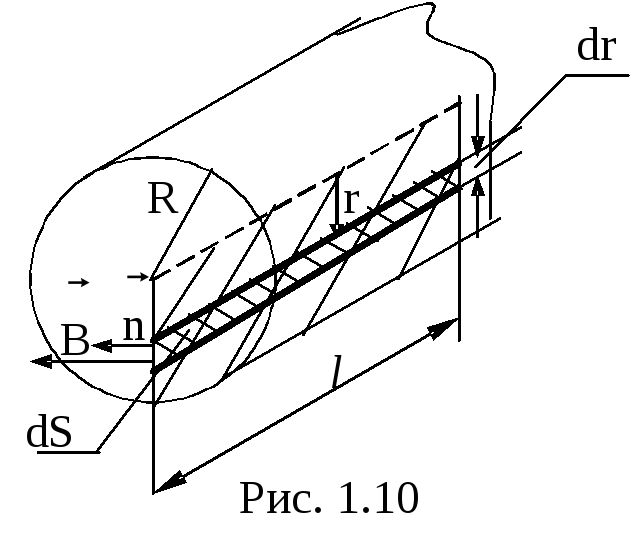ример 4. Постоянный токI=10 А течет по длинному прямому проводнику круглого сечения. Найти поток вектора магнитной индукции через одну из половин осевого сечения в расчете на один метр его длины.

Решение

Воспользуемся результатом решения предыдущей задачи при rR.

.

Выберем вектор нормали к заштрихованной части сечения проводника, чтобы он совпадал с направлением индукции магнитного поля (рис. 1.10). Тогда согласно определению (1.8)

.

Выделим в сечении полоску шириной dr и длиной l, находящуюся на расстоянии r от оси провода. Ввиду малости величины dr , можно считать, что величина индукции магнитного поля в пределах полоски постоянна и равна B(r). Учитывая это, подставим в выражение потока B=(1/2)_ojr и dS=ldr.

.

Теперь найдем магнитный поток, приходящийся на единицу длины проводника

.

Пример 5. Сколько ампер-витков необходимо для получения индукции магнитного поля В=1,4 Тл в электромагните с тороидальным железным сердечником с длиной средней линииL=90 см и воздушным промежутком l_o =5 мм. Рассеянием магнитного потока в воздушном промежутке пренебречь.