
- •«Омский государственный технический университет» Векторная алгебра Омск - 2011
- •Содержание
- •Предисловие
- •1. Векторы и линейные операции над ними
- •1.1. Основные понятия
- •1.2. Линейные операции над геометрическими векторами
- •1.3. Свойства линейных операций
- •1.4. Линейная зависимость между векторами
- •2. Линейные операции над геометрическими векторами в координатной форме
- •2.2. Проекция вектора на ось
- •2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
- •2.4. Координаты вектора в дск
- •2.5. Радиус-вектор точки. Координаты точки в пространстве
- •2.12. Координаты единичного вектора. Направляющие косинусы
- •3. Скалярное произведение двух векторов
- •2. Свойства скалярного произведения.
- •4. Векторное произведение двух векторов
- •2. Свойства векторного произведения
- •4. Физический смысл векторного произведения.
- •5. Смешанное (векторно-скалярное) произведение трёх векторов
- •2. Свойства смешанного произведения.
- •Методические указания к решению задач индивидуальных домашних заданий (идз)
- •Линейные операции над векторами
- •Скалярное произведение двух векторов и его приложения
- •3. Векторное произведение двух векторов и его приложения
- •Смешанное произведение трёх векторов и его приложения
- •7. Индивидуальные домашние задания
- •З а д а ч а 1
- •З а д а ч а 2
- •З а д а ч а 3
- •З а д а ч а 4
- •2. Даны три вектора: ,,.
- •З а д а ч а 5
- •1. Даны три вектора силы: ,,. Найти работу, совершаемую равнодействующей этих сил при перемещении
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •1. Даны вершины треугольника ,,. Вычис-
- •З а д а ч а 9
- •З а д а ч а 10
- •4.1. Контрольные вопросы
- •Список литературы
Смешанное произведение трёх векторов и его приложения
Задача 12. Даны
координаты вершин параллелепипеда
![]()
![]() .
Найти: 1) объём параллелепипеда; 2) высоту,
опущенную из вершины C;
3) угол между вектором
.
Найти: 1) объём параллелепипеда; 2) высоту,
опущенную из вершины C;
3) угол между вектором
![]() и гранью, в которой лежат векторы
и гранью, в которой лежат векторы![]() и
и![]() .
.
Решение.
Определим векторы
![]()
![]() .
.
1
 ).
). .
.
2).
![]()
![]() ?
?![]() ,
, .
.
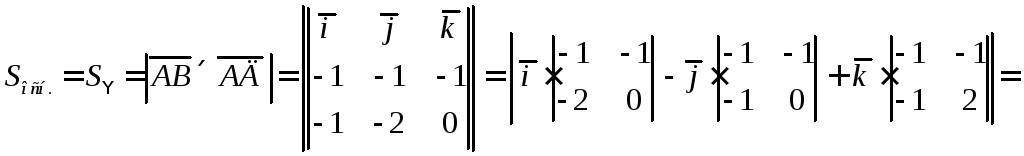
![]() .
Тогда
.
Тогда
![]() .
.
|
|
Для этого определим
угол между вектором
|

![]() .
.
Тогда
 .
.![]() .
.
Угол
![]() ,
т.е.
,
т.е.![]() .
.
Задача 13. Проверить
лежат ли четыре точки
![]()
![]() в одной плоскости.
в одной плоскости.
Решение.
Если точки лежат в одной плоскости, то
и векторы, например,
![]() лежат в одной плоскости, т.е. компланарны,
следовательно, их смешанное произведение
равно 0. Определим векторы:
лежат в одной плоскости, т.е. компланарны,
следовательно, их смешанное произведение
равно 0. Определим векторы:![]() ,
,![]() ,
,![]() .
.
С оставим
определитель:
оставим
определитель:
Определитель
равен нулю, следовательно, векторы
линейно зависимы. Найдём линейную
зависимость, например, вектора
![]() от
от![]() и
и![]() .
.![]() .
.

 .
Тогда
.
Тогда
 .
.
Получим
![]()
![]()
![]() .
Тогда
.
Тогда![]() .
.
7. Индивидуальные домашние задания
Индивидуальные домашние задания выполняется по графику, разработанному кафедрой «Высшая математика», и соответствуют обязательной части практической работы второго раздела программы первого семестра.
Решения задач необходимо представлять в письменном виде в отдельных тетрадях. Нумерация задач должна совпадать с их нумерацией в задании.
В работе должны быть указаны условия задач и развёрнутое решение с пояснениями.
Защита ИДЗ для студентов дневной формы обучения проводится в виде контрольных работ на практических занятиях или на консультациях.
Во время защиты студент должен ответить на контрольные вопросы, пояснить решения задач из заданий, решить аналогичные задачи.
Повторная защита для студентов дневной формы обучения проводится на консультациях.
Студенты, не защитившие ИДЗ повторно, защищают их по графику,
составленному преподавателем.
Студенты заочной формы обучения сдают ИДЗ на проверку в межсессионный период.
Защита ИДЗ для студентов заочной формы обучения проводится на консультациях и в экзаменационную сессию.
|
№ |
Тема |
для ДО |
для ЗО |
|
1 |
Линейные операции над векторами |
Задачи 1, 2 |
Задачи 1, 2 |
|
2 |
Скалярное произведение двух векторов и его приложения |
Задачи 3, 4, 5 |
Задачи 4, 5 |
|
3 |
Векторное произведение двух векторов и его приложения |
Задачи 6, 7, 8 |
Задачи 7, 8 |
|
4 |
Смешанное произведение трёх векторов и его приложения |
Задачи 9, 10 |
Задачи 9, 10 |
З а д а ч а 1
1. Дан параллелограмм
ABCD.
Доказать, что
![]() ,
где
,
где
![]()
![]() произвольная точка
пространства.
произвольная точка
пространства.
2. В параллелограмме
ABCD:
![]()
![]() точка пересечения диагоналей. Найти
точка пересечения диагоналей. Найти
![]() ,
если а)
,
если а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
г)
,
г)![]() .
.
3. В ромбе ABCD
диагонали
![]() ,
,![]() .
Разложить по этим двум
.
Разложить по этим двум
векторам векторы
![]() .
.
4. В треугольнике
PQR:
![]() ,
точка
,
точка![]()
![]() середина стороныQR.
Выразить вектор
середина стороныQR.
Выразить вектор
![]() через векторы
через векторы![]() и
и![]() .
.
5. На сторонах ОА
и ОВ
в прямоугольнике ОАСВ
отложены единичные векторы
![]() и
и![]() .
Выразить векторы
.
Выразить векторы![]() и
и![]() через векторы
через векторы![]() и
и![]() ,
если
,
если![]() .
.
6. В треугольнике
АВС:
М
– точка пересечения медиан треугольника,
![]() .
Разложить
.
Разложить![]() и
и![]() по векторам
по векторам![]() и
и![]() .
.
7. В параллелограмме
ABCD
точки K
и М
![]() середины сторонBC
и CD,
середины сторонBC
и CD,
![]() .
Выразить векторы
.
Выразить векторы![]() и
и![]() через векторы
через векторы![]() и
и![]() .
.
8. Точка O
является центром тяжести (точка
пересечения медиан) треугольника АВС.
Доказать, что
![]() .
.
9. В четырёхугольнике ABCD диагонали в точке пересечения делятся пополам. Доказать, что этот четырёхугольник параллелограмм.
10. Четырехугольник
ABCD
– параллелограмм, O
– точка пересечения диагоналей,
![]() и
и![]()
![]() середины параллельных сторонBC
и AD
соответственно. Построить векторы: а)
середины параллельных сторонBC
и AD
соответственно. Построить векторы: а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
г)
,
г)![]() ,
,
д)![]() ,
е)
,
е)![]() .
.
11. В треугольнике
АВС:
![]() ,
,![]() ,
точки
,
точки![]()
![]() середины сторонАВ,
BC
и АС
соответственно. Выразить через векторы
середины сторонАВ,
BC
и АС
соответственно. Выразить через векторы
![]() и
и![]() медианы
медианы
треугольника![]() .
.
12. В треугольнике
![]() вектор
вектор![]() и вектор
и вектор![]() .
Построить каждый из следующих векторов:
1)
.
Построить каждый из следующих векторов:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
13. По данным векторам
![]() и
и![]() построить каждый из следующих векторов:
1)
построить каждый из следующих векторов:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
14. Какому условию
должны удовлетворять векторы
![]() и
и![]() ,
чтобы вектор
,
чтобы вектор![]() делил пополам угол между векторами
делил пополам угол между векторами![]() и
и![]() ?
?
15. Три силы
![]() ,
приложенные к одной точке, имеют взаимно
перпендикулярные направления. Определить
величину их равнодействующей, если
известно, что
,
приложенные к одной точке, имеют взаимно
перпендикулярные направления. Определить
величину их равнодействующей, если
известно, что![]() ,
,![]()
![]() .
.
16. В тетраэдре
ABCD:
![]() ,
,![]() ,
,![]() ,
точка
,
точка![]()
![]() центр тяжести треугольникаАВС.
Выразить вектор
центр тяжести треугольникаАВС.
Выразить вектор
![]() через векторы
через векторы![]() ,
,![]() ,
,![]() .
.
17. Даны точки A,
В и С.
Построить точку
![]() так, чтобы
так, чтобы![]() .
.
18. В треугольнике
АВС
проведена биссектриса AD.
Выразить вектор
![]() через векторы
через векторы![]() и
и![]() .
.
19. В трапеции ABCD
![]() точки
точки![]() и
и![]()
![]() середины оснований
середины оснований![]() и
и![]() ,
,![]()
![]() точка пересечения диагоналей. Выразить
векторы
точка пересечения диагоналей. Выразить
векторы![]() и
и![]()
через
![]() и
и![]() .
.
20. В трапеции ABCD
![]() точки
точки![]() и
и![]()
![]() середины оснований
середины оснований![]() и
и![]() ,
,![]()
![]() точка пересечения диагоналей. Выразить
векторы
точка пересечения диагоналей. Выразить
векторы![]() и
и![]()
через
![]() и
и![]() .
.
21. В трапеции ABCD
![]()
![]()
![]() точка пересечения диагоналей,
точка пересечения диагоналей,![]() и
и![]() .
Выразить векторы
.
Выразить векторы![]() и
и![]() через векторы
через векторы![]() и
и![]() .
.
22. В трапеции ABCD
![]()
![]()
![]() точка пересечения диагоналей,
точка пересечения диагоналей,![]() и
и![]() .
Выразить векторы
.
Выразить векторы![]() и
и![]() через векторы
через векторы![]() и
и![]() .
.
23. В произвольном
треугольнике АВС
точки
![]()
![]() середины
сторон
середины
сторон![]() и
и![]() .
Выразить векторы
.
Выразить векторы![]() ,
,![]() и
и![]() через векторы
через векторы![]() и
и![]() .
.
24. В треугольнике
![]() проведена средняя линия
проведена средняя линия![]() параллельная стороне
параллельная стороне![]() .
Выразить векторы
.
Выразить векторы![]() и
и![]() через векторы
через векторы![]() и
и![]() .
.
25. Пусть ABCD
– параллелограмм, O![]() точка пересечения его диагоналей.
Полагая
точка пересечения его диагоналей.
Полагая
![]() и
и![]() ,
выразить через
,
выразить через![]() и
и![]() векторы
векторы![]() ,
,![]() ,
,![]() ,
,![]() .
.
26. Точка
![]()
![]() центр тяжести треугольникаАВС.
Выразить: 1) вектор
центр тяжести треугольникаАВС.
Выразить: 1) вектор
![]() через
через![]() и
и![]() ;
2) вектор
;
2) вектор![]() через векторы
через векторы![]() и
и![]() .
.
27. В тетраэдре ABCD
точка
![]() лежит на ребре
лежит на ребре![]() и делит отрезок
и делит отрезок![]() в отношении
в отношении![]() ,
,![]() ,
,![]() ,
,![]() .
Выразить векторы
.
Выразить векторы![]() ,
,![]() ,
,![]() через векторы
через векторы![]() ,
,![]() ,
,![]() .
.
28. В тетраэдре ABCD
точка
![]() делит сторону
делит сторону![]() в отношении
в отношении![]() .
Выразить векторы
.
Выразить векторы![]() ,
,![]() ,
,![]() через векторы
через векторы![]() ,
,![]() ,
,![]() .
.
29. Дан треугольник
АВС и
произвольная точка
![]() .
.![]()
![]() середины сторон
середины сторон![]() и
и![]() соответственно. Доказать, что
равнодействующая сил
соответственно. Доказать, что
равнодействующая сил
![]() ,
,
![]() и
и![]() равна равнодействующей сил
равна равнодействующей сил![]() ,
,![]() и
и![]() .
.
30. В параллелограмме
ABCD
![]() и
и
![]()
![]() середины противоположных сторон
середины противоположных сторон![]() и
и![]() ,
,![]()
![]() точка пересечения диагоналей. Выразить
векторы
точка пересечения диагоналей. Выразить
векторы![]() ,
,![]() ,
,![]() ,
,![]() через векторы
через векторы![]() и
и![]() .
.

