
- •«Омский государственный технический университет» Векторная алгебра Омск - 2011
- •Содержание
- •Предисловие
- •1. Векторы и линейные операции над ними
- •1.1. Основные понятия
- •1.2. Линейные операции над геометрическими векторами
- •1.3. Свойства линейных операций
- •1.4. Линейная зависимость между векторами
- •2. Линейные операции над геометрическими векторами в координатной форме
- •2.2. Проекция вектора на ось
- •2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
- •2.4. Координаты вектора в дск
- •2.5. Радиус-вектор точки. Координаты точки в пространстве
- •2.12. Координаты единичного вектора. Направляющие косинусы
- •3. Скалярное произведение двух векторов
- •2. Свойства скалярного произведения.
- •4. Векторное произведение двух векторов
- •2. Свойства векторного произведения
- •4. Физический смысл векторного произведения.
- •5. Смешанное (векторно-скалярное) произведение трёх векторов
- •2. Свойства смешанного произведения.
- •Методические указания к решению задач индивидуальных домашних заданий (идз)
- •Линейные операции над векторами
- •Скалярное произведение двух векторов и его приложения
- •3. Векторное произведение двух векторов и его приложения
- •Смешанное произведение трёх векторов и его приложения
- •7. Индивидуальные домашние задания
- •З а д а ч а 1
- •З а д а ч а 2
- •З а д а ч а 3
- •З а д а ч а 4
- •2. Даны три вектора: ,,.
- •З а д а ч а 5
- •1. Даны три вектора силы: ,,. Найти работу, совершаемую равнодействующей этих сил при перемещении
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •1. Даны вершины треугольника ,,. Вычис-
- •З а д а ч а 9
- •З а д а ч а 10
- •4.1. Контрольные вопросы
- •Список литературы
4. Векторное произведение двух векторов
1. Определение. Векторным произведением двух векторов называется вектор, удовлетворяющий трём условиям:
|
|
1)
3) векторы
|
2. Свойства векторного произведения
|
10.
| ||||||||||||||||||
|
20. множителя. | ||||||||||||||||||
|
30.
| ||||||||||||||||||
|
40.
В
частности,
| ||||||||||||||||||
|
50
Теорема 4. Если
векторы
Доказательство.
Разложим
векторы | ||||||||||||||||||
|
|
| ||||||||||||||||
|
| ||||||||||||||||||
Геометрический смысл векторного произведения.
![]() ;
;
![]() .
.
Замечание:
Векторное
произведение может быть выражено
формулой:
![]() ,
где
,
где![]()
![]() орт направления вектора
орт направления вектора![]() .
.
4. Физический смысл векторного произведения.
|
| |
|
|
Вектор линейной
скорости
колеса
равен векторному произведению
вектора угловой
скорости
|
5. Смешанное (векторно-скалярное) произведение трёх векторов

1. Определение.
Смешанным произведением
трёх векторов, взятых вуказанном поряд
![]() ,
,
называется
число
![]() .
.
Записывается:
![]() =
=![]() .
.
2. Свойства смешанного произведения.
|
10.
|
|
20.
|
|
30.
|
|
40.
Теорема 5.
Если в ДСК
заданы векторы
Дано:
Доказать:
Доказательство.
По определению
Замечание.
Если
если
|
|
50.
Теорема 6. Для
того, чтобы векторы
Дано:
Доказать:
Доказательство.
Из определения
компланарности следует, что векторы
Дано:
Доказать:
Доказательство.
Если
|
Геометрический смысл смешанного произведения.
|
|
2
А
|


 .
.

 ,
ч.т.д.
,
ч.т.д.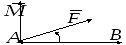 Если сила
Если сила

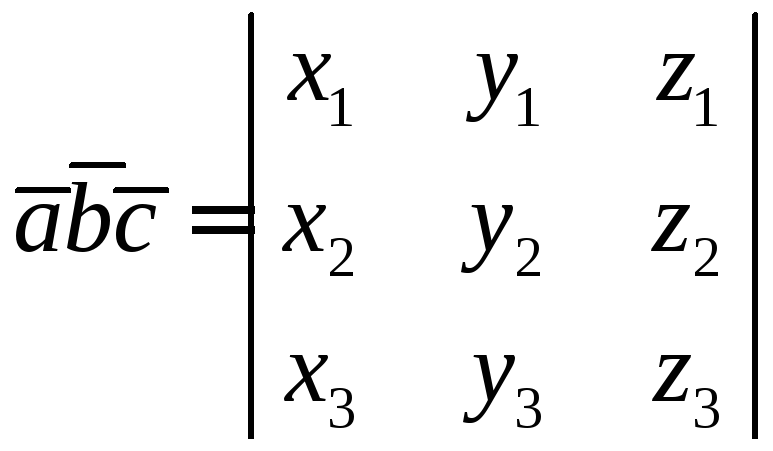 .
. .
. .
Тогда теореме 2.
.
Тогда теореме 2.
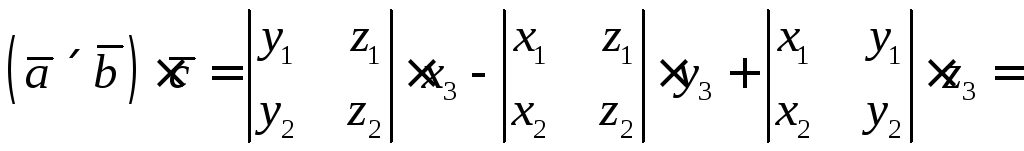
 .
. .
Из этого следует, что строки определителя
линейно зависимы. Тогда векторы так
же линейно зависимы, например,
.
Из этого следует, что строки определителя
линейно зависимы. Тогда векторы так
же линейно зависимы, например, равен модулю
смешанного произведения
векторов
равен модулю
смешанного произведения
векторов
 )
Тетраэдром называется треугольная
пирамида (четырёхгранник).
)
Тетраэдром называется треугольная
пирамида (четырёхгранник).