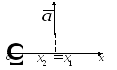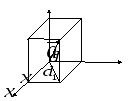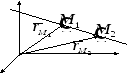- •«Омский государственный технический университет» Векторная алгебра Омск - 2011
- •Содержание
- •Предисловие
- •1. Векторы и линейные операции над ними
- •1.1. Основные понятия
- •1.2. Линейные операции над геометрическими векторами
- •1.3. Свойства линейных операций
- •1.4. Линейная зависимость между векторами
- •2. Линейные операции над геометрическими векторами в координатной форме
- •2.2. Проекция вектора на ось
- •2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
- •2.4. Координаты вектора в дск
- •2.5. Радиус-вектор точки. Координаты точки в пространстве
- •2.12. Координаты единичного вектора. Направляющие косинусы
- •3. Скалярное произведение двух векторов
- •2. Свойства скалярного произведения.
- •4. Векторное произведение двух векторов
- •2. Свойства векторного произведения
- •4. Физический смысл векторного произведения.
- •5. Смешанное (векторно-скалярное) произведение трёх векторов
- •2. Свойства смешанного произведения.
- •Методические указания к решению задач индивидуальных домашних заданий (идз)
- •Линейные операции над векторами
- •Скалярное произведение двух векторов и его приложения
- •3. Векторное произведение двух векторов и его приложения
- •Смешанное произведение трёх векторов и его приложения
- •7. Индивидуальные домашние задания
- •З а д а ч а 1
- •З а д а ч а 2
- •З а д а ч а 3
- •З а д а ч а 4
- •2. Даны три вектора: ,,.
- •З а д а ч а 5
- •1. Даны три вектора силы: ,,. Найти работу, совершаемую равнодействующей этих сил при перемещении
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •1. Даны вершины треугольника ,,. Вычис-
- •З а д а ч а 9
- •З а д а ч а 10
- •4.1. Контрольные вопросы
- •Список литературы
2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
|
Пусть на оси | |
|
1
|
Вектор
|
|
2
|
Вектор
|
|
3
|
Так как
|
|
Составляющая вектора на ось есть вектор равный произведению проекции вектора на ось на орт направления. | |
2.4. Координаты вектора в дск
|
Вектор
т.е.
Z
называется
разложением вектора
x |
|
Замечания:
1) векторы
образом:
|
2.5. Радиус-вектор точки. Координаты точки в пространстве
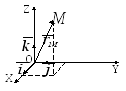
|
|
Определение.
Вектор
Координатами
точки М
будем называть координаты её радиус-
вектора или проекции
|
2.6. Координаты вектора
|
|
Пусть в базисе
заданы точки
Тогда
| ||
|
Чтобы найти координаты вектора надо из координат конца вычесть координаты начала. | |||
|
Аналогино:
| |||
|
|
|
| |
|
|
|
| |
2.7. Линейные операции над векторами
Если в пространстве
задан базис и в нём векторы
![]() и
и![]() ,
то выполнение линейных операций над
векторами сводится к выполнению тех же
операций над
,
то выполнение линейных операций над
векторами сводится к выполнению тех же
операций над
их координатами:
 ,
,
если
![]()
![]() действительное
число, то
действительное
число, то
![]() .
.
2.8. Модуль вектора через координаты
|
Пусть
вектор
| |
|
|
Тогда вектор
Пифагора, получим:
|
2
![]()
|
|
Пусть заданы
точки
Вектор
|
2.10. Деление отрезка в данном отношении
|
Пусть на прямой
|
| |
|
Если
тогда координаты середины отрезка вычисляются по формулам: | ||
|
Если | ||
Условие коллинеарности двух векторов
Условие
коллинеарности двух векторов записывается
в виде
![]() .
.
Если в пространстве
задан базис и в нём векторы
![]() и
и
![]() ,
,
то
![]()
![]()
![]() что равносильно записи:
что равносильно записи:
 Объединяя последние
равенства, получим
Объединяя последние
равенства, получим
 ,
т.е. условие коллинеарности векторов:
,
т.е. условие коллинеарности векторов:

Замечание.
Если два вектора, заданные своими
координатами,
![]() и
и![]() линейно зависимы, то
линейно зависимы, то![]() ,
то их координаты пропорциональны, т.е.
,
то их координаты пропорциональны, т.е. и наоборот, если координаты пропорциональны,
то векторы линейно зависимы.
и наоборот, если координаты пропорциональны,
то векторы линейно зависимы.

 .
. .
. .
. ОА=x,
ОВ=y,
ОС=z.
Составляющие вектора
ОА=x,
ОВ=y,
ОС=z.
Составляющие вектора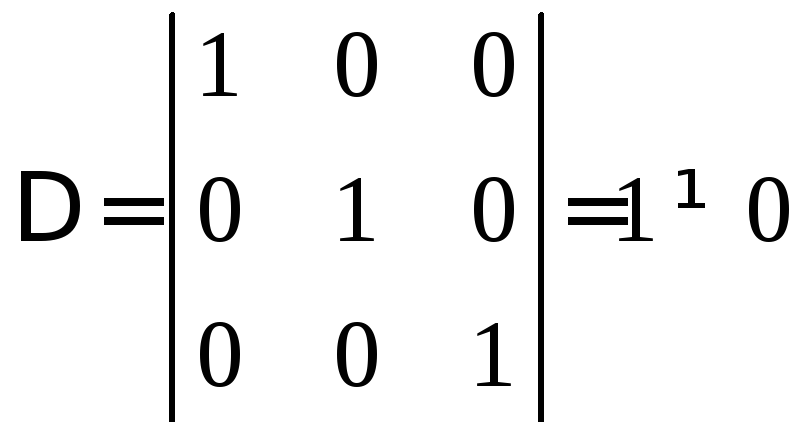 .
Следовательно, векторы
.
Следовательно, векторы
 Замечание 1.
Проекцией вектора
Замечание 1.
Проекцией вектора