
- •«Омский государственный технический университет» Векторная алгебра Омск - 2011
- •Содержание
- •Предисловие
- •1. Векторы и линейные операции над ними
- •1.1. Основные понятия
- •1.2. Линейные операции над геометрическими векторами
- •1.3. Свойства линейных операций
- •1.4. Линейная зависимость между векторами
- •2. Линейные операции над геометрическими векторами в координатной форме
- •2.2. Проекция вектора на ось
- •2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
- •2.4. Координаты вектора в дск
- •2.5. Радиус-вектор точки. Координаты точки в пространстве
- •2.12. Координаты единичного вектора. Направляющие косинусы
- •3. Скалярное произведение двух векторов
- •2. Свойства скалярного произведения.
- •4. Векторное произведение двух векторов
- •2. Свойства векторного произведения
- •4. Физический смысл векторного произведения.
- •5. Смешанное (векторно-скалярное) произведение трёх векторов
- •2. Свойства смешанного произведения.
- •Методические указания к решению задач индивидуальных домашних заданий (идз)
- •Линейные операции над векторами
- •Скалярное произведение двух векторов и его приложения
- •3. Векторное произведение двух векторов и его приложения
- •Смешанное произведение трёх векторов и его приложения
- •7. Индивидуальные домашние задания
- •З а д а ч а 1
- •З а д а ч а 2
- •З а д а ч а 3
- •З а д а ч а 4
- •2. Даны три вектора: ,,.
- •З а д а ч а 5
- •1. Даны три вектора силы: ,,. Найти работу, совершаемую равнодействующей этих сил при перемещении
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •1. Даны вершины треугольника ,,. Вычис-
- •З а д а ч а 9
- •З а д а ч а 10
- •4.1. Контрольные вопросы
- •Список литературы
2. Линейные операции над геометрическими векторами в координатной форме
.2.1. Декартов ортонормированный базис
Определение.
Векторы
![]() образуют правую тройку векторов, если
из конца вектора
образуют правую тройку векторов, если
из конца вектора![]() кратчайший
поворот от вектора
кратчайший
поворот от вектора![]() к вектору
к вектору![]() виден против часовой стрелки и левую
тройку векторов, если кратчайший поворот
виден против часовой стрелки.
виден против часовой стрелки и левую
тройку векторов, если кратчайший поворот
виден против часовой стрелки.
|
|
Рис.5
|
Векторы
на рис.5
|
Определение.
Если в
трехмерном пространстве заданы: 1)
произвольная точка О![]() начало
отсчета и 2) декартов ортонормированный
базис
начало
отсчета и 2) декартов ортонормированный
базис
![]() то
говорят, что в пространстве задана
декартова
прямоугольная система координат.
В дальнейшем, если не оговорено специально,
будем использовать
то
говорят, что в пространстве задана
декартова
прямоугольная система координат.
В дальнейшем, если не оговорено специально,
будем использовать
сокращенную
запись![]() ДСК.
ДСК.
Прямые,
проходящие через начало координат,
называются осями координат: ОХ
![]() ось абсцисс;OY
ось абсцисс;OY![]() ось
ординат;OZ
ось
ординат;OZ![]() ось
аппликат.
ось
аппликат.
Векторы
![]() ,
,![]() ,
,![]()
![]() называются координатными ортами.
называются координатными ортами.
|
координатная прямая |
система координат на плоскости |
система координат в пространстве
|
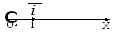
2.2. Проекция вектора на ось
|
Угол
| |||
|
Рис.6
|
| ||
|
Определение.
| |||
|
Определение.
Ортогональнальной проекцией вектора
На рис.8, 9, 10
показаны различные случаи расположения
вектора, при этом проекция
3) 3) | |||
|
Рис.8 |
Рис.9
|
Рис.10 | |
|
Другими словами: | ||
|
1) Вектор
|
2) Вектор
|
3)
|
С
|
10.
|
20.
|
|
30.
| |

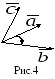






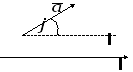
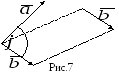
 Ортогональнальной проекцией точки
M
на ось
Ортогональнальной проекцией точки
M
на ось



