
- •«Омский государственный технический университет» Векторная алгебра Омск - 2011
- •Содержание
- •Предисловие
- •1. Векторы и линейные операции над ними
- •1.1. Основные понятия
- •1.2. Линейные операции над геометрическими векторами
- •1.3. Свойства линейных операций
- •1.4. Линейная зависимость между векторами
- •2. Линейные операции над геометрическими векторами в координатной форме
- •2.2. Проекция вектора на ось
- •2.3. Составляющая вектора на оси. Связь между составляющей и проекцией
- •2.4. Координаты вектора в дск
- •2.5. Радиус-вектор точки. Координаты точки в пространстве
- •2.12. Координаты единичного вектора. Направляющие косинусы
- •3. Скалярное произведение двух векторов
- •2. Свойства скалярного произведения.
- •4. Векторное произведение двух векторов
- •2. Свойства векторного произведения
- •4. Физический смысл векторного произведения.
- •5. Смешанное (векторно-скалярное) произведение трёх векторов
- •2. Свойства смешанного произведения.
- •Методические указания к решению задач индивидуальных домашних заданий (идз)
- •Линейные операции над векторами
- •Скалярное произведение двух векторов и его приложения
- •3. Векторное произведение двух векторов и его приложения
- •Смешанное произведение трёх векторов и его приложения
- •7. Индивидуальные домашние задания
- •З а д а ч а 1
- •З а д а ч а 2
- •З а д а ч а 3
- •З а д а ч а 4
- •2. Даны три вектора: ,,.
- •З а д а ч а 5
- •1. Даны три вектора силы: ,,. Найти работу, совершаемую равнодействующей этих сил при перемещении
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •1. Даны вершины треугольника ,,. Вычис-
- •З а д а ч а 9
- •З а д а ч а 10
- •4.1. Контрольные вопросы
- •Список литературы
1.2. Линейные операции над геометрическими векторами
Линейными операциями над векторами называют операцию сложения векторов и операцию умножения вектора на скаляр (число).
|
1. Сложение векторов. |
|
|
|
| ||
|
| ||
|
г)
Правило
параллелограмма: | ||
|
|
с общим началом
понимается вектор
| |
|
2 | ||
|
Под разностью
векторов
с вектором
Другими словами,
это вектор, идущий из
конца «вычитаемого»
вектора в конец
«уменьшаемого»
(вторая диагональ параллелограмма),
Выражение
| ||
|
3. Умножение вектора на число. | ||
|
|
При умножении
вектора на число
| |
1.3. Свойства линейных операций
|
10
коммутативность сложения; |
20
|
|
30
существует
нулевой вектор (нейтральный элемент),
такой что
|
40
существует
противоположный вектор, такой что
|
|
50
|
60
|
|
70
|
80 |
Геометрические
векторы, для которых выполняются две
операции: 1) сложение векторов; 2) умножение
векторов на действительное число,
удовлетворяющие свойствам 10![]() 80,
образуют векторное
пространство.
80,
образуют векторное
пространство.
1.4. Линейная зависимость между векторами
Определение.
Результат
конечного числа линейных операций
![]() называется
линейной
комбинацией
векторов
называется
линейной
комбинацией
векторов
![]() .
Числа
.
Числа
![]() называются
коэффициентами
линейной
комбинации. В равенстве
называются
коэффициентами
линейной
комбинации. В равенстве
![]() вектор
вектор![]() является линейной комбинацией векторов
является линейной комбинацией векторов![]() или вектор
или вектор
![]() линейно выражается через векторы
линейно выражается через векторы![]() .
.
Например, вектор
![]() является линейной комбинацией векторов
является линейной комбинацией векторов![]() с коэффициентами 3, 4,
с коэффициентами 3, 4,![]() 7
соответственно.
7
соответственно.
Определение.
Векторы
![]() называются
линейно
зависимыми,
если существуют числа
называются
линейно
зависимыми,
если существуют числа
![]() ,
среди которых хотя бы одно число отлично
от нуля, и такие, что выполняется:
,
среди которых хотя бы одно число отлично
от нуля, и такие, что выполняется:![]() .
.
Определение.
Векторы
![]() называются
линейно
независимыми,
если равенство
называются
линейно
независимыми,
если равенство
![]() выполняется
только при
выполняется
только при
![]() .
.
Замечания:
1) если хотя бы один из векторов нулевой, то векторы линейно зависимы;
2) если хотя бы один из векторов является линейной комбинацией остальных векторов, то векторы линейно зависимы;
3) два вектора
линейно зависимы![]() когда
они коллинеарны;
когда
они коллинеарны;
4) три вектора
линейно зависимы![]() когда
они компланарны.
когда
они компланарны.
Определение.
Базисом
линейного пространства называется
упорядоченная система векторов
![]() этого пространства, которая удовлетворяет
двум условиям:
этого пространства, которая удовлетворяет
двум условиям:
а) векторы системы
![]() линейно независимы;
линейно независимы;
б) всякий вектор
пространства является линейной
комбинацией векторов системы
![]() .
.
Число векторов
базиса называется размерностью
пространства. Пространство, в котором
базис состоит из
![]() векторов
векторов![]() ,
называется
,
называется
![]() мерным,обозначается
мерным,обозначается
![]() .
Векторы
.
Векторы
![]() называютсябазисными.
Любые n
линейно независимых векторов этого
пространства образуют его базис. Если
задан базис, то каждый вектор
называютсябазисными.
Любые n
линейно независимых векторов этого
пространства образуют его базис. Если
задан базис, то каждый вектор
![]() имеет
единственное разложение по этому базису.
имеет
единственное разложение по этому базису.
Определение.
Пусть n=3,
тогда
![]()
![]() трехмерное векторное пространство.
Базисом в пространстве
трехмерное векторное пространство.
Базисом в пространстве![]() называется любая упорядоченная тройка
некопланарных векторов
называется любая упорядоченная тройка
некопланарных векторов![]() .
Любой вектор
.
Любой вектор![]() этого пространства можно разложить по
данному базису единственным образом,
т.е.
этого пространства можно разложить по
данному базису единственным образом,
т.е.![]() .
.
Определение.
Если
n=2,
то
![]() двумерное пространство (плоскость).
Базисом на плоскости называеся любая
упорядоченная пара неколлинеарных
векторов
двумерное пространство (плоскость).
Базисом на плоскости называеся любая
упорядоченная пара неколлинеарных
векторов![]() и любой вектор этого пространства можно
разложить по данному базису единственным
образом, т.е.
и любой вектор этого пространства можно
разложить по данному базису единственным
образом, т.е.![]() .
.
Определение.
Базисом на
прямой называется любой ненулевой
вектор этой прямой. Пусть базис состоит
из одного вектора![]() Тогда
любой вектор этой прямой будет коллинеарен
вектору,
Тогда
любой вектор этой прямой будет коллинеарен
вектору,![]() а
это означает, что будет выполняться
равенство
а
это означает, что будет выполняться
равенство![]() .
Это равенство означает разложение
вектора
.
Это равенство означает разложение
вектора![]() по
данному базису.
по
данному базису.
|
Замечание.
|

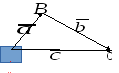 а) Правило
треугольника:
а) Правило
треугольника:
 б) Правило
многоугольника
б) Правило
многоугольника
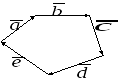 в) Если векторы
образуют замкнутый многоугольник,
как показано на рисунке, то сумма
векторов равна нулю:
в) Если векторы
образуют замкнутый многоугольник,
как показано на рисунке, то сумма
векторов равна нулю:
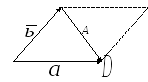 .
Вычитание
векторов.
.
Вычитание
векторов.
 строки
линейно зависимы, значит, определитель
строки
линейно зависимы, значит, определитель