Министерство образования и науки Российской Федерации

Южно-Российский государственный политехнический университет

(НПИ) имени М.И.Платова

Кафедра «Электромеханика и электрические аппараты»

Методическое пособие к лабораторным работам

по курсу

«Электрические и электронные аппараты»

Новочеркасск

ЮРГПУ(НПИ)

2014

²

УДК 621.3(076.5)

Рецензент кандидат техн. наук Феоктистова Т.И.

Медведев В.В., ПалийВ.Я.,Чамлай С.В.

Методическое пособие к лабораторным работам по курсу «Электромеханика и электрические аппараты» / Юж. - Рос. гос. политехн. ун-т (НПИ) имени М.И. Платова. Новочеркасск: ЮРГПУ (НПИ), 2014. – 87с.

Предназначено для проведения лабораторных работ студентам, обучающимся по направлению 140400 «Электроэнергетика и электротехника».

© Южно-Российский государственный

политехнический университет (НПИ) имени

М.И. Платова, 2014-10-30

³

Содержание

Лабораторная работа № 1…………………………………………………..…..4

Исследование контактного переходного сопротивления

Лабораторная работа № 2……………………………………………….…….12

Исследование статических характеристик электромагнита

постоянного тока

Лабораторная работа № 3………………………………………………….….23

Исследование статических характеристик электромагнита

переменного тока

Лабораторная работа № 4……………………………………………….…….31

Реле защиты электроприводов

Лабораторная работа № 5…………………………………….……………….38

Реле времени

Лабораторная работа № 6……………………………………………………..50

Магнитный пускатель

Лабораторная работа № 7…………………………………………...………...58

Электромагнитные контакторы

Лабораторная работа № 8……………………………………………………..68

Установочные автоматы

Лабораторная работа № 9……………………………………………….…….77

Исследование токового реле с магнитоуправляемыми контактами

Лабораторная работа № 10……………………………………………………82

Исследование емкостного датчика углового перемещения

Библиографический список…………………………………………………..87

⁴

Лабораторная работа № 1

ИССЛЕДОВАНИЕ КОНТАКТНОГО ПЕРЕХОДНОГО

СОПРОТИВЛЕНИЯ

Цель работы: исследование зависимости переходного

сопротивления контактов от силы контактного нажатия и от значения тока,

протекающего

материалов.

1. Снять

через замкнутые контакты,

Программа работы

изготовленные из разных

построить зависимость

контактного переходного

P_K

сопротивления Rк от силы контактного нажатия R_K = f (P_K) для контактных пар из различных материалов.

2. Снять и построить зависимость контактного переходного

сопротивления от тока R_к=f(I) при Rк=const для различных контактных пар.

3. Исследовать влияние на величину контактного переходного

сопротивления процесса окисления контактной поверхности от величины

контактного нажатия.

R_K = f (P_K)

4. Рассчитать зависимости для различных контактных пар

и построить на одном графике с опытными.

Пояснения к работе

Наличие в контактном соединений места перехода тока из одного

проводника в другой приводит к увеличению электрического

сопротивления в этом месте по сравнению со сплошным проводником

таких же размеров и формы. Это сопротивление называют контактным

переходным сопротивлением.

Появление контактного переходного сопротивления вызвано, во-

первых, наличием на контактных поверхностях загрязнений и оксидных

⁵

пленок (тогда в цепи появляется дополнительное сопротивление оксидных

пленок) и, во-вторых, тем, что как бы тщательно не были обработаны

(отшлифованы) поверхности контактов, касание контактов будет

происходить не по всей площади рабочей поверхности, называемой

кажущейся или условной, а по отдельным микроплощадкам. Эти площадки

образуются в результате смятия микроскопических бугорков на

поверхности при сдавливании контактов.

Сумма микроплощадок соприкосновения составляет так называемую

поверхность, воспринимающую усилие (физическую поверхность

соприкосновения). Так как ток проходит не через всё сечение, а лишь через

его часть, то сопротивление току возрастает.

Сопротивление, появляющееся в результате стягивания линии тока к

истинной площадке соприкосновения, называется сопротивлением

стягивания R_C .

R_K

может быть

Таким образом, контактное сопротивление

представлено как сумма сопротивления стягивания R_C и сопротивления

посторонних слоёв или плёнок R_ПЛ :

R_K = R_C + R_ПЛ .

Сопротивление R_ПЛ может меняться в процессе эксплуатации в

очень широких пределах. Плёнки, толщина которых δ ≤ 100⁰ А,

ПЛ

проницаемы для туннельного эффекта. Для их характеристики вводится

понятие удельного туннельного сопротивления .

σ

f

Сопротивление таких плёнок равно

σ

f

R_ПЛ =

2

πa

f

,

σ = 5 ⋅10

где a – радиус контактной площадки, см;

-9

– удельное туннельное сопротивление ( Ом·см² – для

f

σ

серебряных контактов).

⁶

-8

f

σ = 1 ⋅10

Обычно считают, что плёнки с Ом·см² не оказывают

влияние на контактное сопротивление.

Плёнки, толщина которых δ_ПЛ ≥ 200⁰ А, являются практически

изоляторами. Ток через замкнутые контакты с такими плёнками будет

протекать при условии их разрушения, в частности – механическим путем

(при проскальзывании контактов).

В теории электрических контактов, наиболее широкое применение

нашла эллиптическая модель контакта.

Для неё сопротивление стягивания определяется выражением:

ρ

2a

R_C = ,

где ρ – удельное электрическое сопротивление материала контакта;

a – радиус контактной площадки.

Эта формула дает погрешность до 5%, если поперечные

размеры контакта превосходят в 10-13 раз диаметр площадки касания.

Практически это условие в большинстве случаев соблюдается.

Если два контакта имеют n площадок соприкосновения, то

ρ

2

n

R_C =

∑^{a .}

K =1

Чтобы определить величину R_c точечного контакта,

необходимо знать число и размеры всех контактных площадок.

Радиус a определяется характером деформации контактов.

Если деформация только упругая, то радиус площадки касания

при сжатии сферических контактов силой Р выражается формулой Герца:

3

3

a = ηPr_Э ,

4

где η – упругая постоянная;

r₁r₂

r₁ + r₂

r_э, r₁, r₂ – радиусы сферических контактов, r_Э = .

⁷

(1.1)

(1.2)

Для контактов из железа, никеля, меди

Pr_Э

E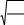

a =1.1³ .

Для контактов из серебра, золота, палладия

Pr_Э

E

a = 0.86³ ,

где Е – модуль упругости.

Эти формулы справедливы для одноточечного контакта.

Если деформация пластическая, то

F

,

a =

(1.3)

определения

π H_B n

где Н_В – твердость по Бринеллю;

n – число площадок соприкосновения.

При небольших контактных нажатиях Р для

радиуса контактной площадки следует использовать формулы (1.1) и (1.2),

а при достаточно больших – формулу (1.3). Граничную силу можно

определить из соотношения

3

58 H_B r_Э

E²

P_ГР = .

Если Р<Р_ГР – деформация считается упругой, в противном случае –

пластичной.

В большинстве случаев при расчете контактного переходного

сопротивления пользуются эмпирическими формулами. Наиболее часто

применяется формула

K_a

R_К = ,

(0.102 P)

m

где К_а – параметр, зависящий от состояния поверхности, материала

контактов;

m – параметр, зависящий от формы поверхности.

⁸

Так для контактов из серебра К_а=60 мкОм·Н, из меди К_а=100 мкОм·Н

(данные для слаботочных плоскостных, точечных, щеточных контактов).

Для сильноточных контактов из меди К_а=400 мкОм·Н. Значения параметра

m могут быть приняты равными: для точечного контакта m=0.5; для

линейного контакта m=0.5÷0.8; для плоскостного контакта m=1.