Практическая работа № 4

Тема: Исследование функций и построение графиков функций.

Цель работы:

1. Закрепление знаний по темам «Предел» и «Производная».

2. Отработка навыков исследования функций с помощью производных и построения графиков.

Литература:

1. Богомолов Н.В. Практические занятия по математике.

2. Дадаян А.А. Математика: Учебник. Глава 9, § 9.9 – 9.14.

3. Конспект лекций.

Время на выполнение: 2 часа.

Содержание работы:

Теоретическая часть.

Основные понятия

Общая схема исследования функции y = f(x).

1. Область определения функции. Найти ее область определения D(f) . Если это не слишком сложно, то полезно найти также область значений E(f) . (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)

2. Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.

3. Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения D(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.

4. Наклонные и горизонтальные асимптоты. Если область определения D(f) включает в себя лучи вида (a;+ ) или (− ;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x + или x − соответственно, т.е. найти Наклонные асимптоты:

, где

Горизонтальные асимптоты:

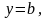где

5. Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближенно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва (промежутки знакопостоянства функции).

6. Нахождение промежутков монотонности.

Признак возрастания (убывания) функции.

Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I.

Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I.

Замечание 1.

Если функция f непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку.

Замечание 2.

Для решения неравенств f'(х)>0 и f'(х)<0 удобно пользоваться обобщением метода интервалов (теоремой Дарбу): точки, в которых производная равна 0 или не существует, разбивают область определения функции f на промежутки, в каждом из которых f' сохраняет постоянный знак. Знак можно определить, вычислив значение f' в какой-нибудь точке промежутка.

7. Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием - локальные минимумы. Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

Точку х₀ называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают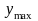 . Точку х₀ называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки х₀ понимают интервал , где -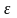 достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.