Действующее значение тока диода I д для всех схем выпрямления определяют по формуле (12).

Амплитудное значение тока диода I _{Д МАКС} определяют из уравнения (6), полагая в нем ωt=0 .

При этом с учетом формулы (7) получим

I _{Д МАКС} = I_н^. F/p (17)

F = (1 – cos θ)/(sin θ – θ^. cos θ) (18)

где F – параметр, зависящий от угла θ и являющийся поэтому функцией параметра А. Зависимость F(A) приведена на рис. 3. Величины I_{Д СР}, I _Д, I _{Д МАКС} для различных схем выпрямления указаны в табл. 3.

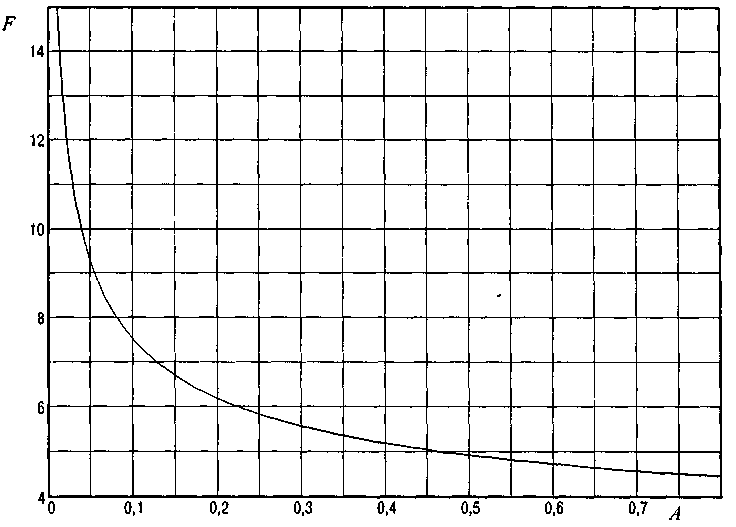
Рис. 3

Обратное напряжение диода Uобр макс определяется выбранной схемой выпрямления и приведено в табл. 3.

Приближенное значение прямого сопротивления диода r_пр должно определяться по статическим вольт-амперным характеристикам выбранного типа диода. При отсутствии таковых прямое сопротивление можно вычислить по приближенной формуле

r_пр = U_{Д ПР} /I_н (19)

Здесь U_{Д ПР} – прямое падение напряжения на диоде, измеренное при протекании тока I_н. Для кремниевых диодов можно принять U_{Д ПР} = 1 В, а для диодов Шоттки – 0,6 В.

Переходим к определению выходных параметров выпрямителя.

Коэффициент пульсаций выпрямленного напряжения может быть определен из следующих соображений.

Так как сопротивление конденсатора для первой гармоники выпрямленного напряжения всегда много меньше сопротивления нагрузки X_C << R_Н, то переменная составляющая тока замкнется в основном через конденсатор. Для высших гармоник сопротивление конденсатора будет еще меньше, и поэтому с достаточной для практических расчетов точностью амплитуду пульсаций по первой гармонике можно определить из следующего выражения:

U_{МАКС 01} = I_{МАКС 01}^. X_C = I_{МАКС 01}/(p C) (20)

где I_{МАКС 01} – амплитуда первой гармоники тока, протекающего через конденсатор. За один период изменения тока питающей сети через конденсатор будет проходить p импульсов тока длительностью 2θ.

Разложив ток конденсатора в ряд Фурье, и взяв первую гармонику разложения, с учетом (20) и (7) получим амплитуду пульсации в виде:

U_{МАКС 01} = U_Н ^. H_p / (r ^. C)

(21)

H_p =(sin p ^. cos  - p cos p ^.sin) ^.10⁶ / ² p(p² – 1)f cos

где H_p – параметр, зависящий от угла  и являющийся, следовательно, функцией параметра А. Зависимость H_p = f(A) для p = 1, 2, 3 приведена на рис. 4.

Рис. 4

Выразив коэффициент пульсации в процентах, получим

k_п = 100 H_p / (r ^. C) % (22)

где С - измеряется в микрофарадах.

Определив по графику рис. 4 значение H_p и задаваясь коэффициентом пульсации на выходе выпрямителя, можно по формуле (22) определить емкость конденсатора, необходимую для получения заданного коэффициента пульсации.

Внешняя ( нагрузочная характеристика) выпрямителя, т.е. зависимость U_н = f(I_н) при U₁ = const , позволяет определить отклонение выходного напряжения, обусловленное изменением тока нагрузки (∆U_н)_I , напряжение холостого хода U_{н х.х}, ток короткого замыкания I_{н к.з}, и внутреннее сопротивление R_В выпрямителя.

Для определения этой зависимости воспользуемся выражениями (5) и (7), представив их в следующем виде:

U_н / U_2макс = cos  и I_н / (pU_2макс / r) = (sin θ – θ^. cos θ)/  = γ₀

Так как величина γ₀ пропорциональна току нагрузки, а cos  пропорционален выпрямленному напряжению, зависимость cos  = f(γ₀), рис. 5, показывает в определенном масштабе зависимость

U_н = f( I_н ), т.е. может рассматриваться как обобщенная внешняя характеристика выпрямителя.

Действительно, если умножить U_2макс на ординаты кривой рис. 5, то получим значения U_н. Умножив абсциссы кривой рис. 5 на pU_2макс / r , получим значение I_н.

Если I_н = 0, то U_н = U_{н х.х} = U_2макс ; при U_н = 0, I_н = I_{н к.з} = pU_2макс / r

Рис. 5

На основании внешней характеристики выпрямителя могут быть определены отклонение выходного напряжения, обусловленное током нагрузки,

(∆U_н)_I = U_{н х.х} - U_н (23)

и его внутреннее сопротивление

R_В = (U_{н х.х} - U_н) / I_н (24)

Рассмотрим теперь особенности расчета выпрямителей при учете активного сопротивления r и индуктивности рассеяния L_S трансформатора.

На рис. 6а приведена эквивалентная схема однотактного трехфазного выпрямителя, а на рис. 6б - временные диаграммы напряжений и токов для этой схемы. При наличии L_S ток i₂ как и в случае L_S = 0, начинается в момент равенства u₂ и U_н, но прекращается после окончания интервала 2 .

Рис. 6

Наличие L_S сказывается не только на длительности, но и на амплитуде тока диода. В соответствии с этим в расчете должно быть учтено соотношение индуктивного и активного сопротивлений фазы выпрямителя:

 = arctg L_S / r.

Все параметры выпрямителя находятся по формулам, аналогичным приведенным ранее для случая L_S = 0, однако параметры A_L, B_L, D_L, F_L и H_pL являются функциями не только угла  , но и угла 

I_н = (pU_нA_L )/( r);

A_L = (I_н r)/( p U_н);

U₂ = U_нB_L;

(25)

I₂ = I_нD_L / p;

I _{Д МАКС} = I_н^. F_L / p;

k_п = 100 H_pL / (r ^. C) %

Графики функций B_L, D_L, F_L, H_pL и cos  = f(γ_0L) приведены на рис. 7.

Рис. 7

После вычисления емкости фильтра необходимо подобрать соответствующий конденсатор по справочнику.