3. Интервальные оценка коэффициентов регрессии

Предположение о нормальном распределении случайных отклонений _i с нулевым математическим ожиданием и постоянной дисперсией, т.е. , позволяет получать не только наилучшие линейные несмещенные точечные оценки (BLUE-оценки) b₀ и b₁ коэффициентов ₀ и ₁ коэффициентов линейного уравнения регрессии, но и находить их интервальные оценки.

Здесь исходят из того, что случайные величины b₀ и b₁ при указанных выше предположениях имеют нормальные распределения:

, .

Тогда выражения

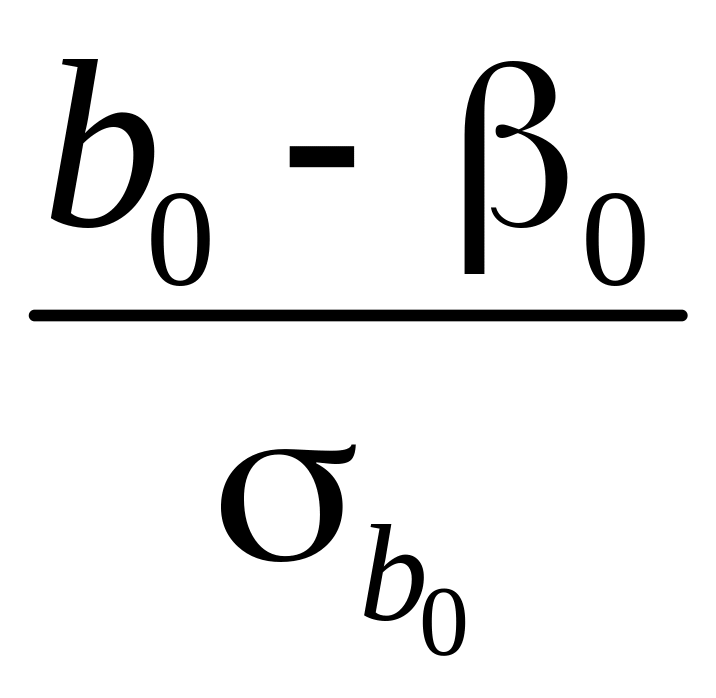и

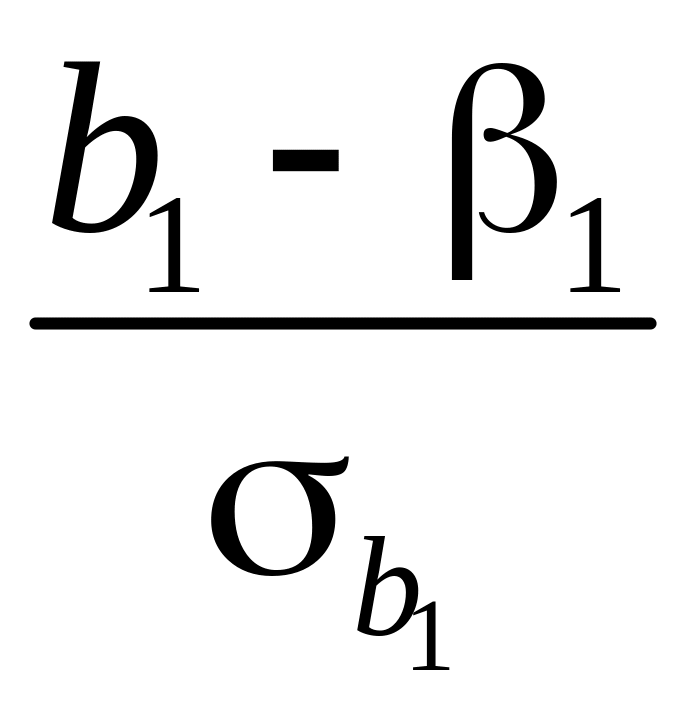
будут иметь стандартное нормальное распределение. Однако в выражениях для b₀ и b₁ дисперсия заменяется ее оценкой S². Поэтому выражения

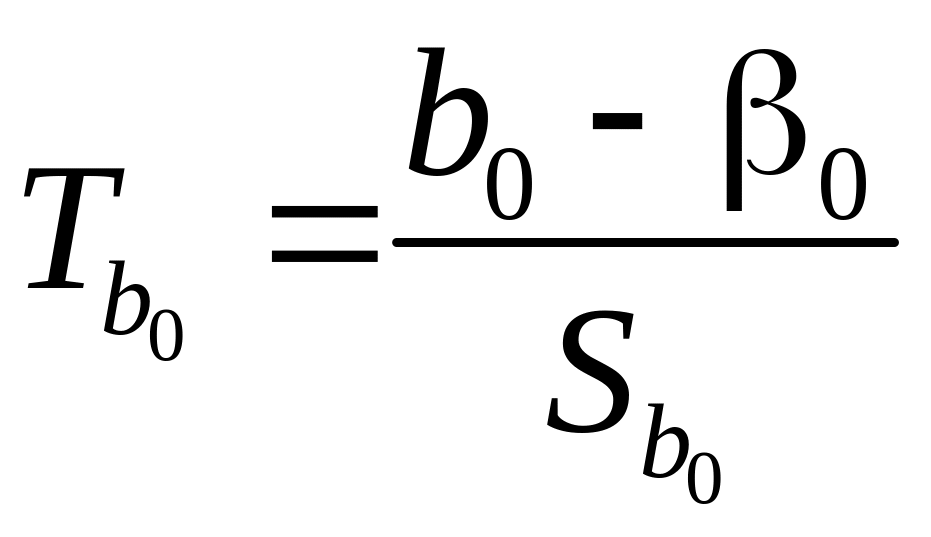и 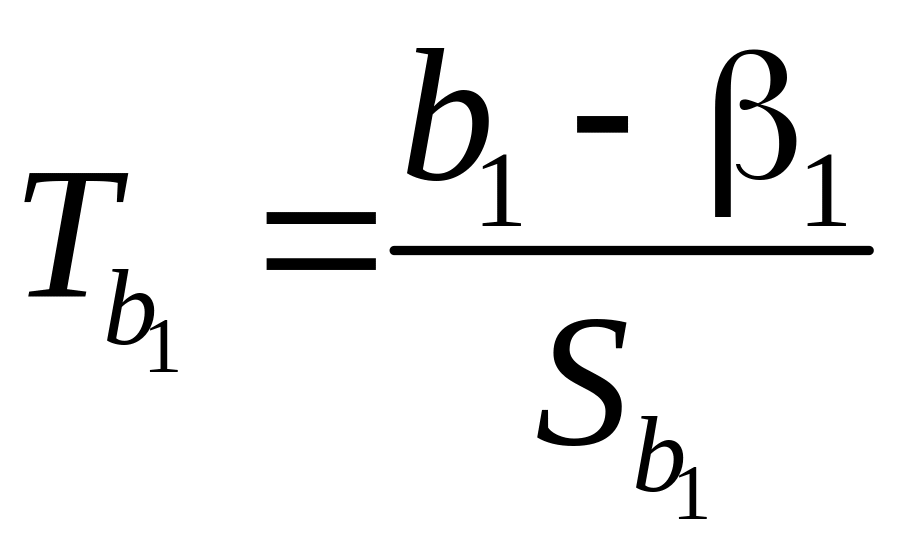(5.42)

будут иметь t-распределение Стьюдента с k=n–2 степенями свободы.

Для построения доверительных интервалов с помощью таблиц критических точек распределения Стьюдента по доверительной вероятности =1– и числу степеней свободы k=n–2 определяют критическое значение , удовлетворяющее условию

. (5.43)

Подставив сюда каждую из формул (5.36), получим

; .

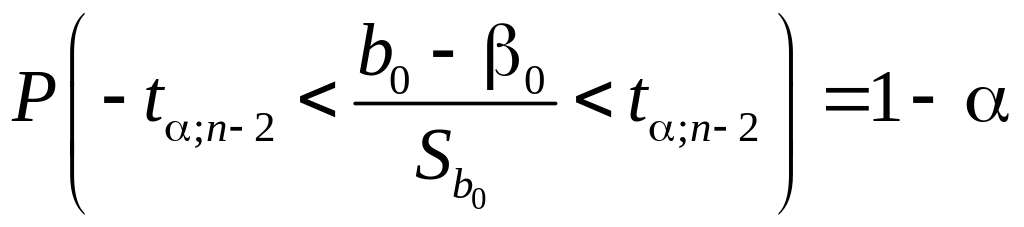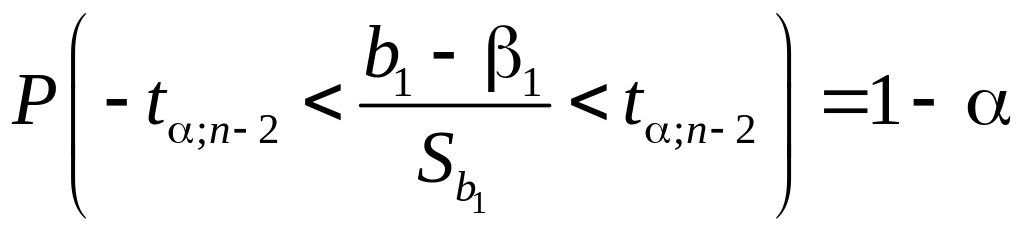После преобразований выражений, стоящих в скобках, имеем:

,

.

Таким образом, доверительные интервалы для коэффициентов регрессии будут иметь следующий вид

, , (5.44)

которые с вероятностью =1– накрывают определяемые параметры ₀ и ₁.

Пример 5.4. Найти интервальные оценки для примера 5.1, 5.3 с уровнем надёжности =0,05.

Решение. В примерах 5.1-5.2 было найдено:

, , , , .

Тогда по формулам (5.46) находим для коэффициента ₀:

; .

Таким образом, с вероятностью 0,95 коэффициент регрессии ₀ принимает значения из интервала . Поскольку ноль также попадает в этот интервал, то, как и следовало ожидать, коэффициент ₀ не является значимым.

Для коэффициента ₁ получаем следующие результаты:

; .

Таким образом, с вероятностью 0,95 коэффициент регрессии ₁ принимает значения из интервала . Поскольку ₁ значительно меньше b₁, то точность прогноза, связанного с этим коэффициентом будет достаточно высокой. 

2. Показатели качества уравнения регрессии

   1. Коэффициент детерминации

После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регрессии. Очевидно, если все точки лежат на построенной прямой, то регрессия Y на X «идеально» объясняет поведение зависимой переменной. В реальной жизни такая ситуация практически не встречается обычно поведение Y лишь частично объясняется влиянием переменной X.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассматривается как самостоятельный метод статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.

Рассмотрим вариацию (разброс) значений y_i вокруг среднего значения . Разобьём эту вариацию на две части: объяснённую регрессионным уравнением и не объяснённую (т.е. связанную с ошибками _i). Тогда получим

(5.45)

Покажем, что третье слагаемое будет равно нулю:

.

Здесь учтено свойства ошибки e_i: и .

Таким образом, справедливо следующее равенство

, (5.46)

где 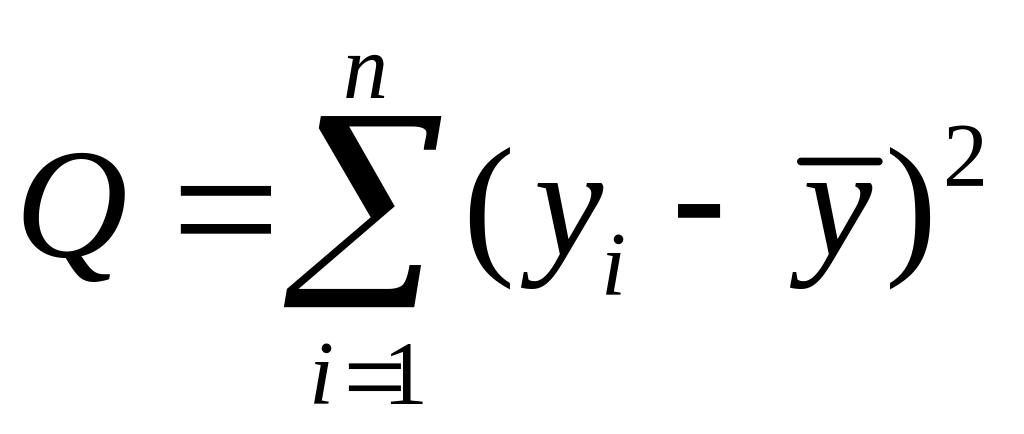– общая сумма квадратов отклонений зависимой переменной от средней, а 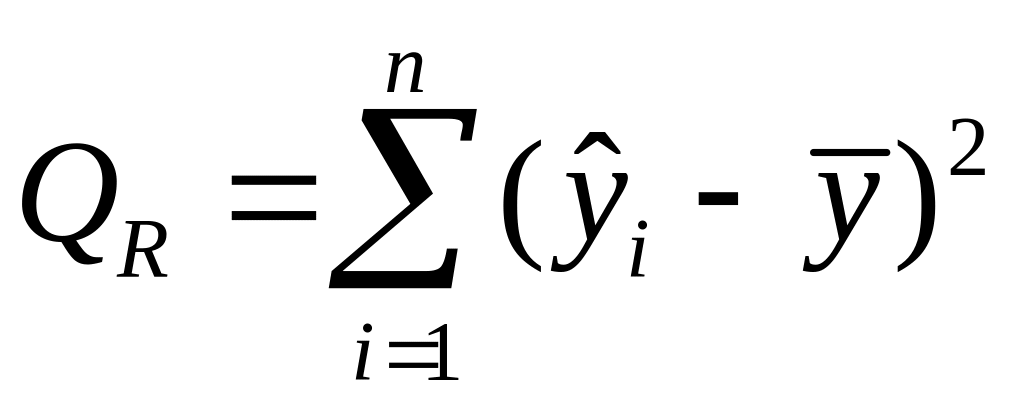и 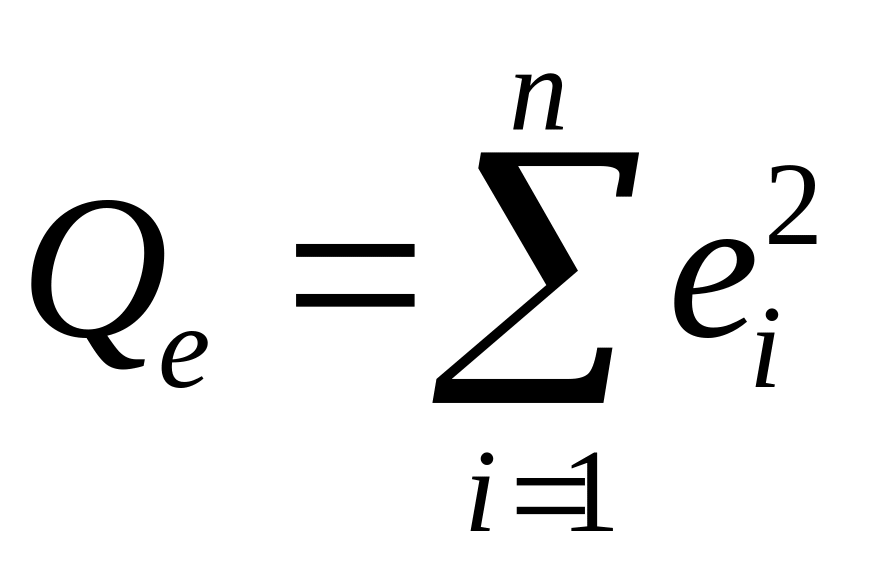– соответственно, сумма квадратов, обусловленная регрессией, и сумма квадратов, характеризующая влияние неучтенных факторов.

Замечание 1. В англоязычной литературе Q, Q_R, Q_e часто обозначаются соответственно TSS (total sum of squares), RSS (regression sum of squares) и ESS (error sum of squares), хотя эти обозначения не являются общепринятыми.

Замечание 2. Равенство (5.46) верно только в том случае, когда константа b₀ включена в число объясняющих параметров регрессии.

Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле

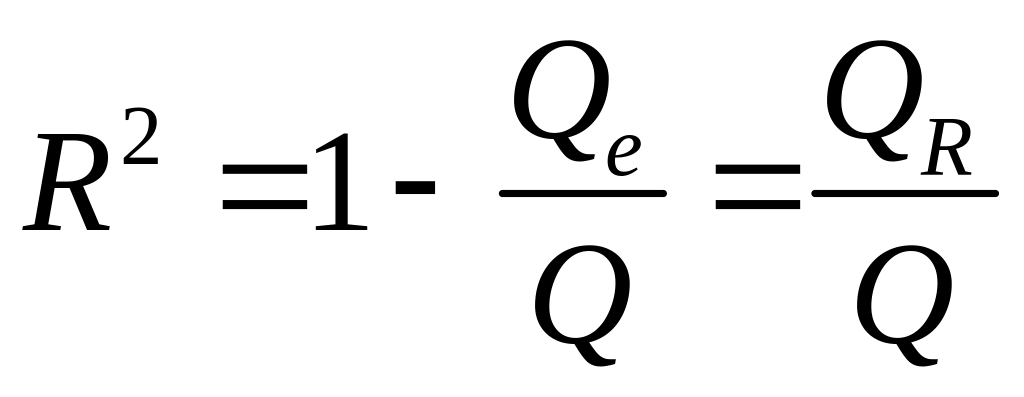. (5.47)

Заметим, что второе равенство в (5.47) верно лишь в том случае, если верно (5.46), т.е. когда константа включена в уравнение регрессии. Только в этом случае имеет смысл рассматривать статистику R².

В силу определения R² принимает значения между 0 и 1, . Чем ближе R² к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если R²=1, то эмпирические точки (x_i,y_i) лежат на линии регрессии и между переменными Y и X существует линейная функциональная зависимость. Если R²=0, то вариация зависимой переменной полностью обусловлена воздействием неучтённых в модели переменных, и линии регрессии параллельна оси абсцисс. Величина R² показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Не следует однако абсолютизировать высокие значения R², т.к. коэффициент детерминации может быть близким к единице в силу того, что обе исследуемые величины X и Y имеют выраженный временной тренд, не связанный с их причинно-следственной зависимостью. В экономике обычно такой тренд имеют объёмные показатели (ВНП, ВВП, доход, потребление). А темповые и относительные показатели (темпы роста, производительность, ставка процента) не всегда имеют тренд. Поэтому при оценивании регрессий по временным рядам объёмных показателей (например, зависимость потребления от дохода или спроса от цены) величина R² может быть весьма близкой к единице. Но это не обязательно свидетельствует о наличии значимой линейной связи между исследуемыми показателями, а может лишь означать лишь то, что поведение зависимой переменной нельзя описать уравнением .

Если уравнение регрессии строится по перекрестным данным, а не по временным рядам, то коэффициент детерминации R² для него обычно не превышает 0,6-0,7. Аналогичные значения R² обычно получаются и для регрессий по временным рядам, если они не имеют выраженного тренда (темп инфляции от уровня безработицы, темпы прироста выпуска от темпов прироста затрат ресурсов и т.п.).

В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т.е. R²=r².

 Действительно,

. 

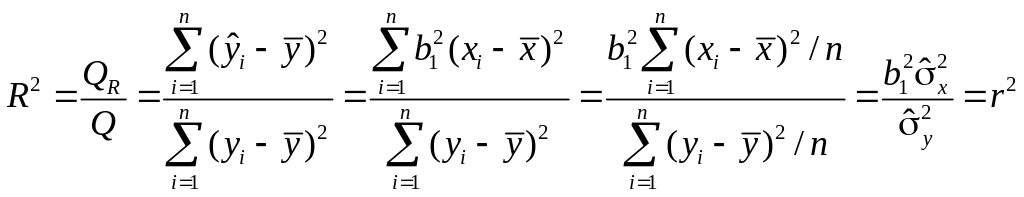Пример 5.5. По данным примеров 5.1-5.4 рассчитать коэффициент детерминации R².

Решение. По формуле (5.71) находим

.

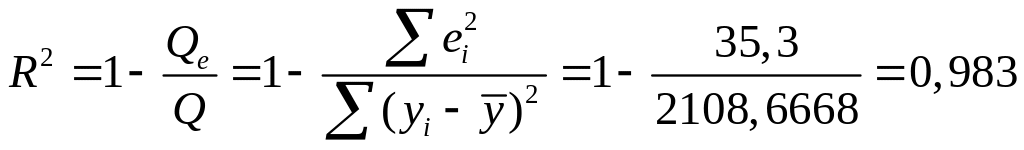Столь высокое значение коэффициента детерминации свидетельствует о высоком общем качестве построенного уравнения регрессии. Отметим, что коэффициент детерминации можно было вычислить и иначе: . 